Penisland, or how to write a spell checker
There is a good article by Peter Norvig in which he tells how to write a spell checker in 20 lines of code. In this article, he shows how search engines can correct errors in queries. And it makes it quite elegant. However, his approach has two serious drawbacks. First, the correction of more than three errors requires large resources. And Google, by the way, does a good job with four errors . Secondly, there is no possibility of checking a coherent text.

So, I want to fix these problems. Namely, write a short phrase or query corrector that:
The rest is under the cut.
')
First, let's solve the problem of finding errors in one word. Suppose we have a dictionary and have a word to check. We can go the way Norvig wrote about:
By generating errors here is meant a rather simple thing. For the word being tested, a set of words is created, which are obtained by using 4 operations: deletion, insertion, replacement and rearrangement. For example, the errors of replacing 'a' with 'o' in the word 'error' will give the following words: error, aaibka, ashabka, ashiak, ashibaa, ashibka. It is clear that this is done for all the letters of the alphabet. Similarly, word variations are generated for insertion, deletion, and permutation.
In this approach, there is one drawback. If you count, then for the English alphabet and the word length of 5 characters, we get about 400 variants of one error. For two errors - 160,000. For three errors - more than six million. And even if a dictionary check occurs in a constant time, such a number of options is too long to generate. Yes, and memory is taken away decently.
We can go the other way: compare the word being checked with each word from the dictionary, using some measure of similarity. Here we can help the distance Levenshteyna . In short, Levenshtein distance is the minimum number of editing operations that need to be applied to the first line to get the second. In the classic version, three operations are considered: insert, delete, and replace. For example, to get “cafe” from the word “cat” we need two operations: one replacement (t-> f) and one insert (-> e).
ca t
ca fe
But there is a catch here. The Levenshtein distance is considered to be O (n * m), where n, m are the lengths of the corresponding rows. Thus, it is not possible to calculate the distance of Levenshtein. However, you can work with this by converting the dictionary into a finite state machine.
Yes, yes, those. And they are needed in order to present the dictionary as a single structure. This structure is very similar to trie, with only minor differences. So, a finite state machine is a kind of logical device that receives a string at the input and allows or rejects it. You can write all this formally, but I will try to do without it so that the form of the formulas does not put anyone to sleep.
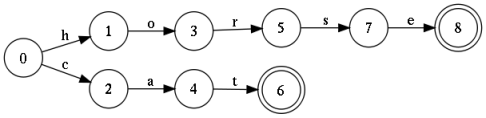
The picture shows an automaton that accepts any finite sequence of characters as input, but allows only two words: 'cat' and 'horse'. Such an automaton is called an acceptor. It is easy to supplement this construction with several thousand words, and as a result you will get a full-fledged dictionary. It is worth noting that this design can be minimized, with the result that it can store hundreds of thousands of words. If the condition of determinism is preserved (arcs that do not have the same labels come out of any state), then the search will be performed in linear time. And this is good.
But a simple acceptor is not enough here. You need to introduce a slightly more intricate design, called a finite state transducer, or a transducer. It differs from an acceptor in that each arc has two symbols: incoming and outgoing. This allows not only to “allow” or “reject” lines, but also to convert the incoming line.

Here is an example of converting the string 'cat' to the string 'fox'.
A converter is a mathematical object. Like a set, or, better said, like a regular expression. Like a regular expression, a transducer defines a specific language, that is, a set of strings. Also, transducers can be crossed, merged, inverted, etc. But unlike a regular expression, it has a very useful operation, called composition.
If to describe informally, the essence of the operation are as follows. We pass simultaneously the first and second transducers, while the characters at the output of the first “feed” to the input of the second. If there is a successful path in both the first and the second transducer, we fix it in the new resultant transducer.
I must say, this is a very informal explanation. However, the formalization will lead to the need to roll out a whole layer of theory, and this was not part of my plans. For formal calculations, you can turn to Wikipedia . Strict formalization is given by Mehryar Mohri . He writes very interesting articles on this topic, although difficult to read.
It is time to go on to explain how this will still help in calculating the Levenshtein distance. It should be noted here that special characters may be involved in the transducer, which denote an empty string (an empty character, we denote it by 'eps'). This will allow us to use them as editing operations. All we need is to arrange the composition of three transducers:
The first two transducers represent incoming lines (see pictures). They allow the words cat and bath .


The error model is a state with reflexive (self-closed) transitions. All of them, with the exception of the a: a transition, represent editing operations:
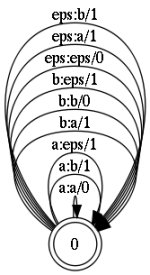
In order not to clutter up the picture, corrections for only two letters are shown on it. Here it should be noted that each transition is labeled with a number. These are weight correction marks. Those. for insert, replace, delete operations, the weight is 1. Whereas for a type transition a: a, which simply translates the original character without correction, the weight is 0. As a result, the final composition takes the following form.
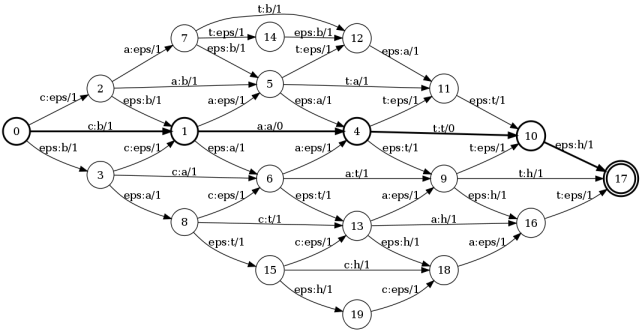
And here is the result: the sum of the weights along the shortest path will be the Levenshtein distance . In this example, this way is: 0 - 1 - 4 - 10 - 17 . The sum of the weights along this path is equal to 2. And now let's follow the marks along this path: c: ba: at: t eps: h. This is nothing more than editing operations. Those. To get the word bath from the word cat, we need to replace the first letter and add the 'h' to the last.
So we can calculate the Levenshtein distance between two transducers. But this means that we can calculate this distance between the line and the dictionary. This will allow you to calculate the closest word in the dictionary and give the correct version of the correction.
How to correct mistakes in individual words is already clear. But how to correct the error when two words stuck together. For example, if instead of Pen Island someone wrote penisland. Moreover, it is necessary to separate these words correctly in order not to injure the gentle psyche of the user. By the way, both Yandex and Rambler cope with the task well , while mail.ru cuts down on the shoulder .
In order to properly segment or merge strings, you need to know which word combination is most likely. In statistical linguistics, so-called language models are used for this, which are usually built on the basis of the ngram model (or Bayesian network). Here I will not explain in detail what it is. The reader can look at my previous post , where such a model is created for a simple text generator.
The good news is that this model can be represented as a transdier. Moreover, there are ready-made libraries that allow you to calculate the model for a given body. The basic idea is to count pairs, triples, or n-sequences of words, transition from frequencies to probabilities, and build an automaton. This automaton does a simple thing - it estimates the probability of a sequence of words at the input. Where probability is greater, that sequence is used.

The figure shows a language model for several words. The picture seems somewhat confusing, but the algorithm for its construction is simple. However, the language model is a topic that requires a separate article. I hope to write it in the near future.
The transition weights in language models are nothing more than the probability of meeting the next word. However, for numerical stability, it is represented by a negative logarithm. Thus, the weights turn into a certain penalty, and the smaller the penalty, the more likely the given string.
We have everything you need to build a spellchecker. All you need to do is to arrange the composition of four transducers:
R = S o E o L o M
and find the shortest path in the resulting transducer R. The path representing the word set will be the desired version of the correction.
There are a couple of points that need clarification. First, the L converter. This is a rather trivial transducer, “gluing” a word out of letters for transferring an entire word to the model. Thus, it helps to move from the letters and symbols of the error model to the words in the language model. The second point is in the scales of converters. In order to produce a correct composition it is necessary that the weights of all the transducers have one meaning. The source line and the lexicon do not have weights, the language model represents probabilities, but here is the Levenshtein error model. We need to move from this estimate to probabilities. This process is close to shamanism, but nevertheless it is possible to choose such weights that are most suited to real errors.
This is probably all. You can rightly ask, but where is the code? And it is not. Everything is done with the help of operations on converters. And these operations are already implemented in libraries. For example, in this: openfst.org . All you need is to build the source objects.
I find this approach very interesting. He has a number of strengths. The first strength is that we do not write code, but simply operate with mathematical objects. This simplifies the development of tools for working with text and saves time.
Another strength is its versatility. No need to write different algorithms for string operations. For example, if you need to determine the errors of the wrong layout of the form “fkujhbnv” -> “algorithm”, then you do not need to write a new program. It is enough to modify the model of errors a little: add transitions marked with letters of two languages and a couple of states.
However, there are also negative sides. It's not trivial enough to achieve stable and fast speed. I could not get. The speed of work is highly dependent on the structure of converters, the number of transitions, the measure of non-determinism. In addition, some converter operations require large amounts of memory. But all these questions are somehow solvable.
Hope the article was helpful. Ask questions if something is not clear. Willingly answer.

So, I want to fix these problems. Namely, write a short phrase or query corrector that:
- able to identify three (and more) errors in the request;
- would be able to check "broken" or "stuck together" phrases, for example expertsexchange - experts_exchange, ma na ger - manager
- didn't require a lot of code to implement
- could be completed to correct errors in other languages and other types of errors
The rest is under the cut.
')
How to identify the error
First, let's solve the problem of finding errors in one word. Suppose we have a dictionary and have a word to check. We can go the way Norvig wrote about:
- believe word in dictionary
- if not, generate single letter errors, and check in the dictionary
- if it fails again, generate two-letter errors, and again in the dictionary
By generating errors here is meant a rather simple thing. For the word being tested, a set of words is created, which are obtained by using 4 operations: deletion, insertion, replacement and rearrangement. For example, the errors of replacing 'a' with 'o' in the word 'error' will give the following words: error, aaibka, ashabka, ashiak, ashibaa, ashibka. It is clear that this is done for all the letters of the alphabet. Similarly, word variations are generated for insertion, deletion, and permutation.
In this approach, there is one drawback. If you count, then for the English alphabet and the word length of 5 characters, we get about 400 variants of one error. For two errors - 160,000. For three errors - more than six million. And even if a dictionary check occurs in a constant time, such a number of options is too long to generate. Yes, and memory is taken away decently.
We can go the other way: compare the word being checked with each word from the dictionary, using some measure of similarity. Here we can help the distance Levenshteyna . In short, Levenshtein distance is the minimum number of editing operations that need to be applied to the first line to get the second. In the classic version, three operations are considered: insert, delete, and replace. For example, to get “cafe” from the word “cat” we need two operations: one replacement (t-> f) and one insert (-> e).
ca t
ca fe
But there is a catch here. The Levenshtein distance is considered to be O (n * m), where n, m are the lengths of the corresponding rows. Thus, it is not possible to calculate the distance of Levenshtein. However, you can work with this by converting the dictionary into a finite state machine.
State machines
Yes, yes, those. And they are needed in order to present the dictionary as a single structure. This structure is very similar to trie, with only minor differences. So, a finite state machine is a kind of logical device that receives a string at the input and allows or rejects it. You can write all this formally, but I will try to do without it so that the form of the formulas does not put anyone to sleep.

The picture shows an automaton that accepts any finite sequence of characters as input, but allows only two words: 'cat' and 'horse'. Such an automaton is called an acceptor. It is easy to supplement this construction with several thousand words, and as a result you will get a full-fledged dictionary. It is worth noting that this design can be minimized, with the result that it can store hundreds of thousands of words. If the condition of determinism is preserved (arcs that do not have the same labels come out of any state), then the search will be performed in linear time. And this is good.
But a simple acceptor is not enough here. You need to introduce a slightly more intricate design, called a finite state transducer, or a transducer. It differs from an acceptor in that each arc has two symbols: incoming and outgoing. This allows not only to “allow” or “reject” lines, but also to convert the incoming line.

Here is an example of converting the string 'cat' to the string 'fox'.
The composition of the machines
A converter is a mathematical object. Like a set, or, better said, like a regular expression. Like a regular expression, a transducer defines a specific language, that is, a set of strings. Also, transducers can be crossed, merged, inverted, etc. But unlike a regular expression, it has a very useful operation, called composition.
If to describe informally, the essence of the operation are as follows. We pass simultaneously the first and second transducers, while the characters at the output of the first “feed” to the input of the second. If there is a successful path in both the first and the second transducer, we fix it in the new resultant transducer.
I must say, this is a very informal explanation. However, the formalization will lead to the need to roll out a whole layer of theory, and this was not part of my plans. For formal calculations, you can turn to Wikipedia . Strict formalization is given by Mehryar Mohri . He writes very interesting articles on this topic, although difficult to read.
Levenshtein distance through composition
It is time to go on to explain how this will still help in calculating the Levenshtein distance. It should be noted here that special characters may be involved in the transducer, which denote an empty string (an empty character, we denote it by 'eps'). This will allow us to use them as editing operations. All we need is to arrange the composition of three transducers:
- first word transducer
- error model transducer
- second word transducer
The first two transducers represent incoming lines (see pictures). They allow the words cat and bath .


The error model is a state with reflexive (self-closed) transitions. All of them, with the exception of the a: a transition, represent editing operations:
- a: a - leave the symbol unchanged
- a: b - replace character; here 'a' on 'b'
- eps: a - insert character
- a: eps - delete character symbol

In order not to clutter up the picture, corrections for only two letters are shown on it. Here it should be noted that each transition is labeled with a number. These are weight correction marks. Those. for insert, replace, delete operations, the weight is 1. Whereas for a type transition a: a, which simply translates the original character without correction, the weight is 0. As a result, the final composition takes the following form.

And here is the result: the sum of the weights along the shortest path will be the Levenshtein distance . In this example, this way is: 0 - 1 - 4 - 10 - 17 . The sum of the weights along this path is equal to 2. And now let's follow the marks along this path: c: ba: at: t eps: h. This is nothing more than editing operations. Those. To get the word bath from the word cat, we need to replace the first letter and add the 'h' to the last.
So we can calculate the Levenshtein distance between two transducers. But this means that we can calculate this distance between the line and the dictionary. This will allow you to calculate the closest word in the dictionary and give the correct version of the correction.
Language model
How to correct mistakes in individual words is already clear. But how to correct the error when two words stuck together. For example, if instead of Pen Island someone wrote penisland. Moreover, it is necessary to separate these words correctly in order not to injure the gentle psyche of the user. By the way, both Yandex and Rambler cope with the task well , while mail.ru cuts down on the shoulder .
In order to properly segment or merge strings, you need to know which word combination is most likely. In statistical linguistics, so-called language models are used for this, which are usually built on the basis of the ngram model (or Bayesian network). Here I will not explain in detail what it is. The reader can look at my previous post , where such a model is created for a simple text generator.
The good news is that this model can be represented as a transdier. Moreover, there are ready-made libraries that allow you to calculate the model for a given body. The basic idea is to count pairs, triples, or n-sequences of words, transition from frequencies to probabilities, and build an automaton. This automaton does a simple thing - it estimates the probability of a sequence of words at the input. Where probability is greater, that sequence is used.

The figure shows a language model for several words. The picture seems somewhat confusing, but the algorithm for its construction is simple. However, the language model is a topic that requires a separate article. I hope to write it in the near future.
The transition weights in language models are nothing more than the probability of meeting the next word. However, for numerical stability, it is represented by a negative logarithm. Thus, the weights turn into a certain penalty, and the smaller the penalty, the more likely the given string.
Putting it all together
We have everything you need to build a spellchecker. All you need to do is to arrange the composition of four transducers:
R = S o E o L o M
- S - source line
- E - error model
- L - Lexicon
- M - language model
and find the shortest path in the resulting transducer R. The path representing the word set will be the desired version of the correction.
There are a couple of points that need clarification. First, the L converter. This is a rather trivial transducer, “gluing” a word out of letters for transferring an entire word to the model. Thus, it helps to move from the letters and symbols of the error model to the words in the language model. The second point is in the scales of converters. In order to produce a correct composition it is necessary that the weights of all the transducers have one meaning. The source line and the lexicon do not have weights, the language model represents probabilities, but here is the Levenshtein error model. We need to move from this estimate to probabilities. This process is close to shamanism, but nevertheless it is possible to choose such weights that are most suited to real errors.
This is probably all. You can rightly ask, but where is the code? And it is not. Everything is done with the help of operations on converters. And these operations are already implemented in libraries. For example, in this: openfst.org . All you need is to build the source objects.
Conclusions, pro et contra
I find this approach very interesting. He has a number of strengths. The first strength is that we do not write code, but simply operate with mathematical objects. This simplifies the development of tools for working with text and saves time.
Another strength is its versatility. No need to write different algorithms for string operations. For example, if you need to determine the errors of the wrong layout of the form “fkujhbnv” -> “algorithm”, then you do not need to write a new program. It is enough to modify the model of errors a little: add transitions marked with letters of two languages and a couple of states.
However, there are also negative sides. It's not trivial enough to achieve stable and fast speed. I could not get. The speed of work is highly dependent on the structure of converters, the number of transitions, the measure of non-determinism. In addition, some converter operations require large amounts of memory. But all these questions are somehow solvable.
Hope the article was helpful. Ask questions if something is not clear. Willingly answer.
Source: https://habr.com/ru/post/105450/
All Articles