Binary search in graphs

Binary search is one of the most basic algorithms known to me. Having a sorted list of comparable items and a target item, the binary search looks in the middle of the list and compares the value with the target item. If the goal is larger, we repeat with the lower half of the list, and vice versa.

For each comparison, the binary search algorithm splits the search space in half. Thanks to this there will always be no more

l o g (n)

$\ log (n)$ comparisons with runtime

O (l o g n)

$O (\ log n)$ . Beautiful, effective, useful.

But you can always look at a different angle.

')

What if I try to perform a binary search on a graph? Most graph search algorithms, such as wide or deep search, require linear time and were thought up by pretty smart people. Therefore, if a binary search by a graph has any meaning, then it should use more information than the one that ordinary search algorithms have access to.

For a binary list search, this information is the fact that the list is sorted, and to control the search, we can compare numbers with the item we are looking for. But in fact, the most important information is not related to the comparability of the elements. It lies in the fact that we can get rid of half the search space at each stage. The stage “comparison with target value” can be perceived as a black box responding to requests like “Is this the value I was looking for?” With the answers “Yes” or “No, but look better here”

If the answers to our queries are quite useful, that is, they allow us to separate large amounts of search space at each stage, then it looks like we got a good algorithm. In fact, there is a natural model of graphs, defined in the article Emamjome-Zade, Kempe, and Singel 2015 as follows.

We receive as input an undirected weighted graph.

G = (V, E)

$G = (V, E)$ with weights

w_{e}

$w_e$ at

e i n E

$e \ in E$ . We see the whole graph and can ask questions in the form of "Is a vertex

v

$v$ necessary to us? "Answers can have two options:

Yes (we won!)
No, but $e = (v, w)$ is the edge of $v$ on the shortest path from $v$ to the desired vertex.

Our goal is to find the right vertex for the minimum number of queries.

Obviously, this only works if

G

$G$ is a connected graph, but small variations in the article will work for unrelated graphs. (In general, this is not true for directed graphs.)

When a graph is a line, the task is “reduced” to a binary search in the sense that the same basic idea is used as in the binary search: we start from the middle of the graph, and the edge we get in response to the query tells us in which half count to continue the search.

And if we make this example a bit more complicated, then the generalization will become obvious:

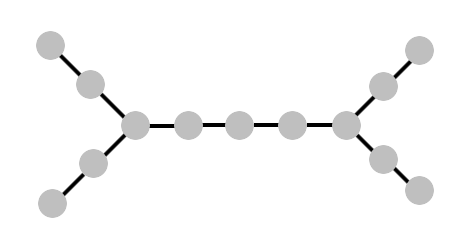
Here we start again from the “central peak” and the answer to our inquiry will relieve us of one of the two halves. But how then do we choose the next vertex, because now we do not have a linear order? It should be obvious - choose the “central top” of any half in which we find ourselves. This choice can be formalized into a rule that will work even in the absence of obvious symmetry, and as it turns out, this choice will always be the right one.

Definition: median weighted graph

G

$G$ relative to a subset of vertices

S s u b s e t V

$S \ subset V$ is the top

v i n V

$v \ in V$ (not necessarily located in

S

$S$ ), which minimizes the sum of the distances between vertices in

S

$S$ >. More formally, it minimizes

P h i_{S} (v) = s u m_{u i n S} d (v, u)

$\ Phi_S (v) = \ sum_ {u \ in S} d (v, u)$

Where

d (u, v)

$d (u, v)$ - sum of edge weights along the shortest path from

v

$v$ before

u

$u$ .

The generalization of a binary search to such a model with queries on the graph leads us to the following algorithm, which limits the search space by querying the median at each step.

Algorithm: binary search in columns. The input data is a graph.

G = (V, E)

$G = (V, E)$ .

We start with a lot of candidates $S = v$ .
Until we found the right vertex and :
- Requesting median $v$ sets $S$ and stop if we find the desired vertex.
- Otherwise, let $e = (v, w)$ will be the edge received in response to the query; calculate the set of all vertices $x \ in V$ for which $e$ is the shortest path of $v$ at $x$ . Call this set $T$ .
- Replace $S$ on $S \ cap t$ .
Print the only remaining vertex in $S$

Indeed, as we will soon see, implementing in Python will be almost as simple. The most important part of the work is to calculate the median and the set

T

$T$ . Both of these operations are small varieties of the Dijkstra algorithm for computing the shortest paths.

A theorem that is simple and well formulated by Emamjome-Zadeh and his colleagues (about half of the page on page 5 in total) is that the algorithm requires only

O (l o g (n))

$O (\ log (n))$ queries - the same as in the binary search.

Before we dive into the implementation, it’s worth considering one trick. Even despite the fact that we are guaranteed to be no more

l o g (n)

$\ log (n)$ queries, because of our implementation of Dijkstra’s algorithm, we definitely won’t have a logarithmic time algorithm. What would be useful in such a situation?

Here we will use the “theory” - we will create a fictional task, for which we will later find application (which is quite successfully used in computer science). In this case, we will treat the request mechanism as a black box. It will be natural to imagine that requests are time-consuming and are a resource that needs to be optimized. For example, as the authors wrote in an additional article , the graph can be a multitude of groupings of a set of data, and requests require the intervention of a person looking at the data and telling which classer should be divided, or which two clusters should be combined. Of course, the graph is too large to handle when grouped, so the median search algorithm must be implicitly defined. But the most important thing is clear: sometimes a request is the most expensive part of the algorithm.

Well, let's implement it all! The full code, as always on Github .

We implement the algorithm

We start with a small variation of Dijkstra’s algorithm. Here we are given the “starting” point as input, and as output we create a list of all the shortest paths to all possible final vertices.

We will start with a bare graph data structure.

from collections import defaultdict from collections import namedtuple Edge = namedtuple('Edge', ('source', 'target', 'weight')) class Graph: #      def __init__(self, vertices, edges=tuple()): self.vertices = vertices self.incident_edges = defaultdict(list) for edge in edges: self.add_edge( edge[0], edge[1], 1 if len(edge) == 2 else edge[2] #   ) def add_edge(self, u, v, weight=1): self.incident_edges[u].append(Edge(u, v, weight)) self.incident_edges[v].append(Edge(v, u, weight)) def edge(self, u, v): return [e for e in self.incident_edges[u] if e.target == v][0]

Now, since most of the work in the Dijkstra algorithm is to track the information accumulated when searching on a graph, we define an “output” data structure — a dictionary with edge weights, along with backward pointers to the shortest paths found.

 class DijkstraOutput: def __init__(self, graph, start): self.start = start self.graph = graph #        v self.distance_from_start = {v: math.inf for v in graph.vertices} self.distance_from_start[start] = 0 #        #        self.predecessor_edges = {v: [] for v in graph.vertices} def found_shorter_path(self, vertex, edge, new_distance): #        self.distance_from_start[vertex] = new_distance if new_distance < self.distance_from_start[vertex]: self.predecessor_edges[vertex] = [edge] else: # ""     self.predecessor_edges[vertex].append(edge) def path_to_destination_contains_edge(self, destination, edge): predecessors = self.predecessor_edges[destination] if edge in predecessors: return True return any(self.path_to_destination_contains_edge(e.source, edge) for e in predecessors) def sum_of_distances(self, subset=None): subset = subset or self.graph.vertices return sum(self.distance_from_start[x] for x in subset)

Dijkstra’s real algorithm then performs a wide search (controlled by priority queue) by

G

$G$ by updating metadata while finding shorter paths.

 def single_source_shortest_paths(graph, start): '''             .   DijkstraOutput. ''' output = DijkstraOutput(graph, start) visit_queue = [(0, start)] while len(visit_queue) > 0: priority, current = heapq.heappop(visit_queue) for incident_edge in graph.incident_edges[current]: v = incident_edge.target weight = incident_edge.weight distance_from_current = output.distance_from_start[current] + weight if distance_from_current <= output.distance_from_start[v]: output.found_shorter_path(v, incident_edge, distance_from_current) heapq.heappush(visit_queue, (distance_from_current, v)) return output

Finally, we implement subroutines for finding the median and computing

T

$T$ :

 def possible_targets(graph, start, edge): '''     G = (V,E),   v  V   e,  v,    w, ,  e      v  w. ''' dijkstra_output = dijkstra.single_source_shortest_paths(graph, start) return set(v for v in graph.vertices if dijkstra_output.path_to_destination_contains_edge(v, edge)) def find_median(graph, vertices): '''    output    ,         ''' best_dijkstra_run = min( (single_source_shortest_paths(graph, v) for v in graph.vertices), key=lambda run: run.sum_of_distances(vertices) ) return best_dijkstra_run.start

And now the core of the algorithm

 QueryResult = namedtuple('QueryResult', ('found_target', 'feedback_edge')) def binary_search(graph, query): '''          "  x  ?"    -  "   !",  "       ". ''' candidate_nodes = set(x for x in graph.vertices) #  while len(candidate_nodes) > 1: median = find_median(graph, candidate_nodes) query_result = query(median) if query_result.found_target: return median else: edge = query_result.feedback_edge legal_targets = possible_targets(graph, median, edge) candidate_nodes = candidate_nodes.intersection(legal_targets) return candidate_nodes.pop()

Here is an example of running a script on a sample graph, which we used above in a post:

 '''        ak bj cfghi dl em ''' G = Graph(['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm'], [ ('a', 'b'), ('b', 'c'), ('c', 'd'), ('d', 'e'), ('c', 'f'), ('f', 'g'), ('g', 'h'), ('h', 'i'), ('i', 'j'), ('j', 'k'), ('i', 'l'), ('l', 'm'), ]) def simple_query(v): ans = input("  '%s'  ? [y/N] " % v) if ans and ans.lower()[0] == 'y': return QueryResult(True, None) else: print("     " " '%s'   . : " % v) for w in G.incident_edges: print("%s: %s" % (w, G.incident_edges[w])) target = None while target not in G.vertices: target = input("   '%s': " % v) return QueryResult( False, G.edge(v, target) ) output = binary_search(G, simple_query) print("  : %s" % output)

The query function simply displays a reminder about the structure of the graph and asks the user to answer (yes / no) and report the corresponding edge if in case of a negative answer.

Execution Example:

'g' ? [y/N] n
    

      
      
      
    

  'g' . :
    

      
      
      
    

  e: [Edge(source='e', target='d', weight=1)]
    

      
      
      
    

  i: [Edge(source='i', target='h', weight=1), Edge(source='i', target='j', weight=1), Edge(source='i', target='l', weight=1)]
    

      
      
      
    

  g: [Edge(source='g', target='f', weight=1), Edge(source='g', target='h', weight=1)]
    

      
      
      
    

  l: [Edge(source='l', target='i', weight=1), Edge(source='l', target='m', weight=1)]
    

      
      
      
    

  k: [Edge(source='k', target='j', weight=1)]
    

      
      
      
    

  j: [Edge(source='j', target='i', weight=1), Edge(source='j', target='k', weight=1)]
    

      
      
      
    

  c: [Edge(source='c', target='b', weight=1), Edge(source='c', target='d', weight=1), Edge(source='c', target='f', weight=1)]
    

      
      
      
    

  f: [Edge(source='f', target='c', weight=1), Edge(source='f', target='g', weight=1)]
    

      
      
      
    

  m: [Edge(source='m', target='l', weight=1)]
    

      
      
      
    

  d: [Edge(source='d', target='c', weight=1), Edge(source='d', target='e', weight=1)]
    

      
      
      
    

  h: [Edge(source='h', target='g', weight=1), Edge(source='h', target='i', weight=1)]
    

      
      
      
    

  b: [Edge(source='b', target='a', weight=1), Edge(source='b', target='c', weight=1)]
    

      
      
      
    

  a: [Edge(source='a', target='b', weight=1)]
    

      
      
      
    

  'g': f
    

      
      
      
    

  'c' ? [y/N] n
    

      
      
      
    

  'c' . :
    

      
      
      
    

  [...]
    

      
      
      
    

  'c': d
    

      
      
      
    

  'd' ? [y/N] n
    

      
      
      
    

  'd' . :
    

      
      
      
    

  [...]
    

      
      
      
    

  'd': e
    

      
      
      
    

  : e

Probabilistic history

The binary search implemented by us in this post is quite minimalistic. In fact, the more interesting part of Emamjome-Zade's work with colleagues is the part in which the answer to the request may be incorrect with an unknown probability.

In this case, there may be a set of shortest paths that are the correct answer to the request, in addition to all the incorrect answers. In particular, this excludes the strategy of transmitting the same request several times and selecting the most popular answer. If the error frequency is 1/3, and there are two shortest paths to the desired vertex, then we can get a situation in which we will see three answers with equal frequency and will not be able to figure out which one is false.

Instead, Emamjome-Zade and his co-authors use a technique based on the algorithm of updating multiplicative weights ( he is back in business! ). Each query gives a multiplicative increase (or decrease) for a set of nodes that are constant, desired vertices, provided that the answer to the query is correct. There are some more details and post-processing to avoid incredible results, but in general, the basic idea is this. Its implementation will be an excellent exercise for readers interested in learning more deeply from this recent article (or pondering their mathematical muscles)

But if you look even deeper, this model of “requesting and receiving advice on how to improve the result” is the classical learning model first formally studied by Dana Engluin. In her model, an algorithm is designed for training the classifier. Valid queries are membership and equivalence queries. Affiliation is, in essence, the question “What is the label of this element?”, And the equivalence query looks like “Is this a correct classifier?” If the answer is “no”, then an example with the wrong label is passed.

This is different from the usual machine learning assumption, because the learning algorithm has to create an example about which it wants more information, and not just rely on a randomly generated subset of data. The goal is to minimize the number of queries until the algorithm exactly learns the desired hypothesis. And in fact - as we saw in this post, if we have a little extra time to study the problem space, then we can create queries that receive a lot of information.

The model of binary search by graphs presented here is a natural analogue of the equivalence query in the search problem: instead of a counter-example with an incorrect label, we get a “push” in the right direction to the goal. Pretty good!

Here we can go in different ways: (1) implement a version of the algorithm with multiplicative weights, (2) apply this technique to the task of ranking or grouping, or (3) consider in more detail theoretical models of learning such as belonging and equivalence.

Source: https://habr.com/ru/post/344144/

All Articles

Binary search in graphs

We implement the algorithm

Probabilistic history

More articles: