A simple algorithm for determining the intersection of two segments

Introduction

In the old days, I was fond of computer graphics, both 2x and 3-dimensional, including mathematical visualizations. What is called just for fun, as a student, wrote a program visualizing N-dimensional figures, rotating in any dimensions, although I was only enough to identify points for a 4-D hypercube. But this is only a saying. The love of geometry has remained with me since then to this day, and I still love to solve interesting problems in interesting ways.

One of these tasks came to me in 2010. The task itself is rather trivial: it is necessary to find out if two 2-D segments intersect, and if they intersect, find their intersection point. More interesting is the decision, which, I think, turned out to be quite elegant, and which I want to offer to the reader. I do not pretend to the originality of the algorithm (although I would like to), but I could not find such solutions online.

Task

Two segments are given, each of which is given by two points: (v11, v12), (v21, v22). It is necessary to determine whether they intersect, and if they intersect, find their intersection point.

Decision

First you need to determine whether the segments intersect. The necessary and sufficient intersection condition that must be met for both segments is as follows: the end points of one of the segments must lie in different half-planes if the plane is divided by the line on which lies the second of the segments. Let's demonstrate this by drawing.



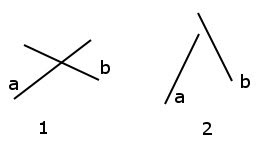
In the left figure (1) two segments are shown, for both of which the condition is met, and the segments intersect. In the right (2) figure, the condition is met for segment b, but for segment a, it is not met, and the segments do not intersect, respectively.

It may seem that to determine which side of the line the point lies from is a non-trivial task, but fear has large eyes and everything is not so difficult. We know that the vector multiplication of two vectors gives us a third vector, the direction of which depends on whether the positive or negative angle between the first and second vectors, respectively, such an operation is anti-commutative. And since all the vectors on the XY plane, their vector product (which must be perpendicular to the vectors to be multiplied) will have only non-zero component Z, respectively, and the difference between the products of vectors will be only in this component. Moreover, when changing the order of multiplication of vectors (read: the angle between the multiplied vectors), it will consist solely in changing the sign of this component.

Therefore, we can multiply the pairwise vectorial vector of the dividing segment by vectors directed from the beginning of the dividing segment to both points of the segment under test.



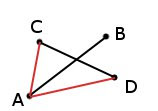
If the Z components of both products have a different sign, then one of the angles is less than 0 but greater than -180, and the second is greater than 0 and less than 180, respectively, the points lie on opposite sides of the line. If the components Z of both products have the same sign, then they also lie on one side of the line.

If one of the components of Z is zero, then we have a boundary case where the point lies exactly on the line being checked. Let the user decide whether he wants to consider this an intersection.

Then we need to repeat the operation for another segment and a straight line, and make sure that the location of its end points also satisfies the condition.

So, if everything is good and both segments satisfy the condition, then the intersection exists. Let's find it, and the vector product will also help us in this.

Since in the vector product we only have a nonzero component Z, its module (the length of the vector) will be numerically equal to this component. Let's see how to find the intersection point.



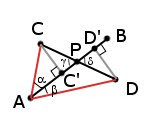
The length of the vector product of vectors a and b (as we found out, numerically equal to its component Z) is equal to the product of the moduli of these vectors and the sine of the angle between them (| a | | b | sin (ab)). Accordingly, for the configuration in the figure we have the following: | AB x AC | = | AB || AC | sin (α), and | AB AB AD | = | AB || AD | sin (β). | AC | sin (α) is the perpendicular dropped from point C to segment AB, and | AD | sin (β) is perpendicular dropped from point D to segment AB (leg ADD '). Since the angles γ and δ are vertical angles, they are equal, which means that the triangles PCC 'and PDD' are similar, and, accordingly, the lengths of all their sides are equally proportional.

Having Z1 (AB x AC, which means | AB || AC | sin (α)) and Z2 (AB x AD, which means | AB || AD | sin (β)), we can calculate CC '/ DD' ( which will be equal to Z1 / Z2), and also knowing that CC '/ DD' = CP / DP, you can easily calculate the location of point P. Personally, I do it as follows:



Px = Cx + (Dx-Cx) * | Z1 | / | Z2-Z1 |;

Py = Cy + (Dy-Cy) * | Z1 | / | Z2-Z1 |;

')

That's all. It seems to me that it is really very simple and elegant. In conclusion, I want to give the function code that implements this algorithm. The function uses a homemade template vector <typename, int>, which is a vector template of dimension int with components like typename. Those interested can easily adjust the function to their vector types.

1 template<typename T>  2 bool are_crossing(vector<T, 2> const &v11, vector<T, 2> const &v12, vector<T, 2> const &v21, vector<T, 2> const &v22, vector<T, 2> *crossing)  3 {  4   vector<T, 3> cut1(v12-v11), cut2(v22-v21);  5   vector<T, 3> prod1, prod2;  6  7   prod1 = cross(cut1 * (v21-v11));  8   prod2 = cross(cut1 * (v22-v11));  9 10   if(sign(prod1[Z]) == sign(prod2[Z]) || (prod1[Z] == 0) || (prod2[Z] == 0)) //      11     return false; 12 13   prod1 = cross(cut2 * (v11-v21)); 14   prod2 = cross(cut2 * (v12-v21)); 15 16   if(sign(prod1[Z]) == sign(prod2[Z]) || (prod1[Z] == 0) || (prod2[Z] == 0)) //      17     return false; 18 19   if(crossing) { // ,      20     (*crossing)[X] = v11[X] + cut1[X]*fabs(prod1[Z])/fabs(prod2[Z]-prod1[Z]); 21     (*crossing)[Y] = v11[Y] + cut1[Y]*fabs(prod1[Z])/fabs(prod2[Z]-prod1[Z]); 22   } 23 24   return true; 25 }