Dissect t-SNE
While working on the article “Deep Learning in R ...” , I repeatedly mentioned the mention of t-SNE - the mysterious technique of nonlinear dimension reduction and visualization of multidimensional variables (for example, here ), I was intrigued and decided to understand everything in detail. t-SNE is t-distributed stochastic neighbor embedding . The Russian version with the “introduction of neighbors” to some extent sounds ridiculous, so I will continue to use the English acronym.
The t-SNE algorithm, also referred to as multi-featured training, was published in 2008 (ref. 1 at the end of the article) by Dutch researcher Lawrence van der Maaten (currently working on Facebook AI Research) and neuron network magician Jeffrey Hinton. The classic SNE was proposed by Hinton and Rowis in 2002 (Ref. 2). The 2008 article describes several “tricks” that simplify the process of finding global minima and improve the quality of visualization. One of these was the replacement of the normal distribution with the Student’s distribution for low-dimensional data. In addition, a successful implementation of the algorithm was made (the article has a link to MatLab), which was then ported to other popular environments .
Let's start with the “classic” SNE and formulate the problem. We have a data set with points that are described by a multidimensional variable with the dimension of space substantially greater than three. It is necessary to obtain a new variable that exists in two-dimensional or three-dimensional space, which would maximally preserve the structure and patterns in the original data. SNE begins with the conversion of the multidimensional Euclidean distance between points into conditional probabilities, reflecting the similarity of points. Mathematically, it looks like this (formula 1):
')

This formula shows how close the point X j is to point X i with a Gaussian distribution around X i with a given deviation σ. Sigma will be different for each point. It is chosen so that the points in areas with higher density have less variance. For this purpose, the evaluation of perplexia is used :

Where H (Pi) - Shannon entropy in bits (formula 2):

In this case, the perplexion can be interpreted as a smoothed estimate of the effective number of "neighbors" for point X i . It is set as a parameter of the method. The authors recommend using a value in the range from 5 to 50. Sigma is determined for each pair of X i and X j using a binary search algorithm .
For two-dimensional or three-dimensional "colleagues" of the pair X i and X j , let's call them for clarity Y i and Y j , it is not difficult to estimate the conditional probability using the same formula 1. The standard deviation is proposed to be set to 1 / √2:

If the mapping points Y i and Y j correctly simulate the similarity between the original points of high dimension X i and X j , then the corresponding conditional probabilities p j | i and q j | i will be equivalent. As an obvious assessment of the quality with which q j | i reflects p j | i , divergence or a Kullback-Leibler distance is used. SNE minimizes the sum of such distances for all display points with a gradient descent. The loss function for this method will be determined by the formula 3:

At the same time, the gradient looks surprisingly simple:

The authors propose the following physical analogy for the optimization process: All display points are connected by springs. The stiffness of the spring connecting points i and j depends on the difference between the similarity of two points in a multidimensional space and two points in a display space. In this analogy, the gradient is the resultant force acting on a point in the display space. If the system is “let go”, after some time it will come into balance, this will be the desired distribution. Algorithmically, the search for equilibrium is proposed to take into account the moments:

where η is the parameter that determines the learning rate (step length), and α is the coefficient of inertia. Using the classic SNE allows you to get good results, but can be associated with difficulties in optimizing the loss function and the problem of crowding (in the original - the crowding problem). t-SNE, if it does not solve these problems at all, it makes it much easier. The t-SNE loss function has two principal differences. First, t-SNE has a symmetric form of similarity in a multidimensional space and a simpler version of the gradient. Secondly, instead of the Gaussian distribution for points from the display space, the t-distribution (Student) is used, whose “heavy” tails facilitate optimization and solve the problem of crowding.
As an alternative to minimizing the sum of Kullback-Leibler divergences between the conditional probabilities p i | j and q i | j, it is proposed to minimize a single divergence between the joint probability P in the multidimensional space and the joint probability Q in the display space:

where p ii and q ii = 0, p ij = p ji , q ij = q ji for any i and j, and p ij is determined by the formula:

where n is the number of points in the data set. The gradient for symmetric SNE is much simpler than for the classic:

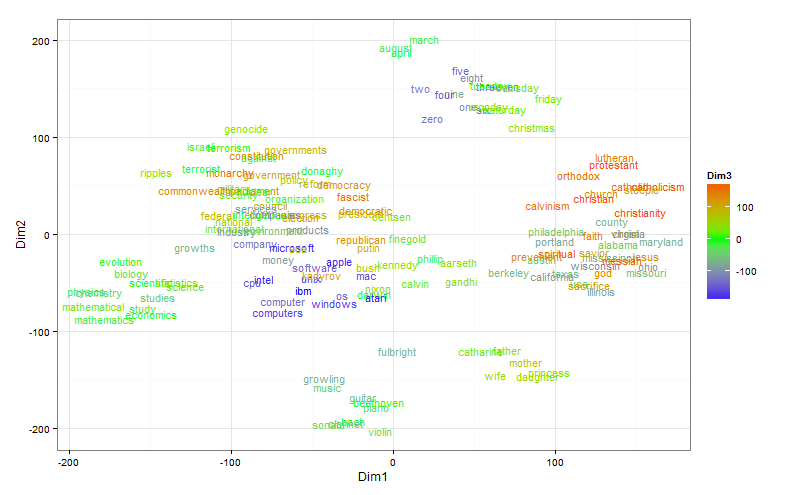
The problem of crowding is that the distance between two points in the display space corresponding to two middle-distance points in a multidimensional space must be significantly larger than the distance that allows us to obtain a Gaussian distribution. Problem solve student's tails. In t-SNE, a t-distribution with one degree of freedom is used. The joint probability for the display space in this case will be determined by formula 4:
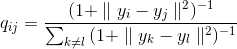
And the corresponding gradient is 5:

Returning to the physical analogy, the resultant force, defined by formula 5, will significantly tighten the points of the display space for nearby points of the multidimensional space, and push them away for the remote ones.
In a simplified form, the t-SNE algorithm can be represented by the following pseudocode:
To improve the result it is proposed to use two tricks. The first authors called the "early compression." His task is to make the points in the display space at the beginning of the optimization be as close as possible to each other. When the distance between the display points is small, it is much easier to move one cluster across another. It is much easier to explore the optimization space and “aim” at global minima. Early compression is created due to the additional L2-penalty as a function of losses, which is proportional to the sum of the squares of the display point distances from the origin (I did not find this in the source code).
The second trick is less obvious - “early hyper-strength” (in the original - “early exaggeration”). It consists in multiplying at the beginning of the optimization of all p ij by some integer number, for example, by 4. The idea is to get larger q ij for large p ij . This will allow for clusters in the source data to obtain dense and widely separated clusters in the display space.
As the source code, I took the original MatLab implementation of van der Maaten. However, my MatLab academic license is long over, so I ported all the code to R. The code is available in the repository . Also at my disposal was the code from the archive of the tsne R-package, took from there a couple of ideas.
For experiments it is proposed to use the following parameters:
Number of iterations: 1000;
Perplexia: 40;
Early hypergrowth: x4 for the first 50 iterations;
Moment α: 0.5 for the first 250 iterations, 0.8 for the remaining 750;
Learning rate η: originally 100 (in the original code - 500) and changes after each iteration in accordance with the scheme described by Robert Jacobs in 1988 (ref. 3).
The algorithm can be divided into three logical parts:
I will illustrate only the most important constructions. First of all, it is necessary to calculate the matrix of squares of the Euclidean distance for the initial data set. For this, it is better to use the rdist () function from the fields package. It works many times faster than the popular dist () from the basic stats package. Perhaps this is due to the fact that it is optimized for the Euclidean distance. Next, you need to initialize the display space. This can be done with the help of rnorm () with a zero mat. expectation and standard deviation 1e-4.
The calculation of the logarithm of perplexia and the Gaussian core is as follows:
The last expression is obtained if formula (1) for p j | i is substituted with formula (2) for perplexion. Let n be the number of points in the source data. Di is the vector of length n-1, with squares of pairwise distances for the line of the original data. It turns out with the help of the construction Di <- D [i, -i] , where D is the matrix of squares of distances nxn, and if i = 1, then Di is the first row of the matrix D without the first column. The kernel, P is a vector, the length is n-1, and the logarithm of perplexion is a real number (due to the sum of elementary products). The original code uses the natural logarithm, I decided to do the same.
For the search for gamma, there are the following restrictions - the number of attempts (divisions) is no more than 50, the threshold difference between the logarithms of a given and the calculated perplexion is 1e-5. One iteration of the binary search is as follows:
gammamin and gammamax are initially set to - and + Inf .
The loss function is calculated as the sum of the rows of the elementwise product of two nxn matrices:
P is a symmetric version of the joint probability for a multidimensional space, calculated as P = .5 * (P + t (P)) from the conditional pairwise probability, t is the matrix transposition operator. Q - joint probability for the display space:
Y is the initialized matrix of points nx 2 for the two-dimensional mapping space. Q is obtained by the nxn matrix by using rdist () .
The gradient is calculated in vectorized form for all Yi at once:
Here, grads is a matrix, the size of nx 2, which is formed by the matrix product. The construction in parentheses is an nxn matrix, on the main diagonal of which are row-by-line sums of the matrix L, and all other elements are taken with a minus sign. The matrix product allows us to multiply by the difference Y i and Y j and immediately calculate the sums of j (formula 4). True gradient is obtained opposite sign.
To search for optimal Y values, something similar to the delta-bar-delta heuristics is used. Its meaning is to adaptively change the step of learning. If the gradient does not change its sign at the next iteration, the step increases linearly (0.2 is added to the gain), if the sign changes, it decreases exponentially (the coefficient is multiplied by 0.8). Given that the gradient we have is the opposite sign:
I could not try to repeat the experiment described in the article (link 1). The idea of this experiment is to visualize the cluster structure for a set of MNIST images. One part of this set contains 60000 images of handwritten numbers from 0 to 9, 28x28 pixels. The data set can be downloaded from the site of the neuron network guru, Jan Lekun.
With loading in R it is necessary to tinker, but the readBin function () which allows to read (and write) the binary data helps. 20 random numbers:

As in the original experiment, I did not use the entire set, but only 6000 images selected randomly using the sample () function. 1000 iterations took a little less than one and a half hours on x64 c Intel Core i7 2.4 GHz. Result on the picture:

Colors are set using labels, MNIST is a marked set of data. The result can be significantly improved. As the authors advise, for the initial set of points, the main component analysis (PCA) should be done and the first 30 should be selected:

There are several PCA implementations for R. The simplest version is in two lines:
The speed of the algorithm is proportional to the square of the number of points. If this amount is reduced, the result will not be as obvious, but quite acceptable. Let's say 2000 points are processed in just 9 minutes.
The t-SNE technique would probably not be so popular if it were not for the ability to visualize the distributed representation of words. In this experiment, I used a relatively small model (about 900 words and a 300-dimensional feature space), trained with the help of word2vec .

Here the size is bigger. A three-dimensional display space is used, the third dimension is represented by color. Words can be considered close if they are located side by side and have the same shade.
It turns out that with a distributed representation of words prepared on real data, everything is not so simple. There are two problems: as a rule, a very large number of clusters and significant differences in their size. For visualization, you can make a random sample, but the result will most likely not be representative. The authors explain this with the following example: If A, B and C are equidistant points in multidimensional space, but there are points between A and B and there is no point between B and C, the algorithm is more likely to combine A and B into one cluster than B and C.
But it so happens that it is visibility that is important, not the fullness of the picture. Then, instead of a random sample of points, you can try to select interesting clusters. Clustering is built into the original word2vec, besides you can use k-means. Perhaps this option does not seem quite "fair", but, in my opinion, has the right to exist. Sampling data for a distributed representation of words from fifteen clusters does not look so confusing:
For large data sets, there is a special implementation of t-SNE, in which the nearest-neighbor trees and the random walk method are used to calculate the similarity in multidimensional space (described in article 1). In practice, you can use the Rtsne package, a wrapper for the C ++ implementation of the Barnes-Hut-SNE. Rtsne can process all 60000 MNIST images in less than an hour. Details can be found in publication 6.
I have not experimented with Rtsne yet, but I have tested tsne (MatLab port of R code). The visualization is much worse than my version. Looking into the package archive, I discovered two things: First, when calculating the Gaussian core, the distance is used without a square, and second, the matrix product is used in the expression for perplexion. In my version and in the code for MatLab, it is elementwise. It is strange that generally turned out visible clusters. I explain this by the “survivability” of the algorithm, but I admit that I did not fully understand something. I would be happy to comment and wish you all impressive multidimensional visualizations.
Formulas for this article are prepared using the online formula editor LATEX .
The t-SNE algorithm, also referred to as multi-featured training, was published in 2008 (ref. 1 at the end of the article) by Dutch researcher Lawrence van der Maaten (currently working on Facebook AI Research) and neuron network magician Jeffrey Hinton. The classic SNE was proposed by Hinton and Rowis in 2002 (Ref. 2). The 2008 article describes several “tricks” that simplify the process of finding global minima and improve the quality of visualization. One of these was the replacement of the normal distribution with the Student’s distribution for low-dimensional data. In addition, a successful implementation of the algorithm was made (the article has a link to MatLab), which was then ported to other popular environments .
A bit of math
Let's start with the “classic” SNE and formulate the problem. We have a data set with points that are described by a multidimensional variable with the dimension of space substantially greater than three. It is necessary to obtain a new variable that exists in two-dimensional or three-dimensional space, which would maximally preserve the structure and patterns in the original data. SNE begins with the conversion of the multidimensional Euclidean distance between points into conditional probabilities, reflecting the similarity of points. Mathematically, it looks like this (formula 1):
')

This formula shows how close the point X j is to point X i with a Gaussian distribution around X i with a given deviation σ. Sigma will be different for each point. It is chosen so that the points in areas with higher density have less variance. For this purpose, the evaluation of perplexia is used :

Where H (Pi) - Shannon entropy in bits (formula 2):

In this case, the perplexion can be interpreted as a smoothed estimate of the effective number of "neighbors" for point X i . It is set as a parameter of the method. The authors recommend using a value in the range from 5 to 50. Sigma is determined for each pair of X i and X j using a binary search algorithm .
For two-dimensional or three-dimensional "colleagues" of the pair X i and X j , let's call them for clarity Y i and Y j , it is not difficult to estimate the conditional probability using the same formula 1. The standard deviation is proposed to be set to 1 / √2:

If the mapping points Y i and Y j correctly simulate the similarity between the original points of high dimension X i and X j , then the corresponding conditional probabilities p j | i and q j | i will be equivalent. As an obvious assessment of the quality with which q j | i reflects p j | i , divergence or a Kullback-Leibler distance is used. SNE minimizes the sum of such distances for all display points with a gradient descent. The loss function for this method will be determined by the formula 3:

At the same time, the gradient looks surprisingly simple:

The authors propose the following physical analogy for the optimization process: All display points are connected by springs. The stiffness of the spring connecting points i and j depends on the difference between the similarity of two points in a multidimensional space and two points in a display space. In this analogy, the gradient is the resultant force acting on a point in the display space. If the system is “let go”, after some time it will come into balance, this will be the desired distribution. Algorithmically, the search for equilibrium is proposed to take into account the moments:

where η is the parameter that determines the learning rate (step length), and α is the coefficient of inertia. Using the classic SNE allows you to get good results, but can be associated with difficulties in optimizing the loss function and the problem of crowding (in the original - the crowding problem). t-SNE, if it does not solve these problems at all, it makes it much easier. The t-SNE loss function has two principal differences. First, t-SNE has a symmetric form of similarity in a multidimensional space and a simpler version of the gradient. Secondly, instead of the Gaussian distribution for points from the display space, the t-distribution (Student) is used, whose “heavy” tails facilitate optimization and solve the problem of crowding.
As an alternative to minimizing the sum of Kullback-Leibler divergences between the conditional probabilities p i | j and q i | j, it is proposed to minimize a single divergence between the joint probability P in the multidimensional space and the joint probability Q in the display space:

where p ii and q ii = 0, p ij = p ji , q ij = q ji for any i and j, and p ij is determined by the formula:

where n is the number of points in the data set. The gradient for symmetric SNE is much simpler than for the classic:

The problem of crowding is that the distance between two points in the display space corresponding to two middle-distance points in a multidimensional space must be significantly larger than the distance that allows us to obtain a Gaussian distribution. Problem solve student's tails. In t-SNE, a t-distribution with one degree of freedom is used. The joint probability for the display space in this case will be determined by formula 4:
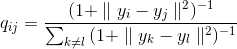
And the corresponding gradient is 5:

Returning to the physical analogy, the resultant force, defined by formula 5, will significantly tighten the points of the display space for nearby points of the multidimensional space, and push them away for the remote ones.
Algorithm
In a simplified form, the t-SNE algorithm can be represented by the following pseudocode:
Data: data set X = {x1, x2, ..., xn},
loss function parameter: Perp perplex
Optimization parameters: the number of iterations T, the learning rate η, the moment α (t).
Result: data representation Y (T) = {y1, y2, ..., yn} (in 2D or 3D).
begin
calculate the pairwise similarity of pj | ic by Perp perplexion (using formula 1)
set pij = (pj | i + pi | j) / 2n
initialize Y (0) = {y1, y2, ..., yn} points of normal distribution (mean = 0, sd = 1e-4)
for t = 1 to T do
calculate the similarity of points in the space of the map qij (according to formula 4)
calculate the gradient δCost / δy (according to the formula 5)
set Y (t) = Y (t-1) + ηδCost / δy + α (t) (Y (t-1) - Y (t-2))
end
end
To improve the result it is proposed to use two tricks. The first authors called the "early compression." His task is to make the points in the display space at the beginning of the optimization be as close as possible to each other. When the distance between the display points is small, it is much easier to move one cluster across another. It is much easier to explore the optimization space and “aim” at global minima. Early compression is created due to the additional L2-penalty as a function of losses, which is proportional to the sum of the squares of the display point distances from the origin (I did not find this in the source code).
The second trick is less obvious - “early hyper-strength” (in the original - “early exaggeration”). It consists in multiplying at the beginning of the optimization of all p ij by some integer number, for example, by 4. The idea is to get larger q ij for large p ij . This will allow for clusters in the source data to obtain dense and widely separated clusters in the display space.
Implementation on R
As the source code, I took the original MatLab implementation of van der Maaten. However, my MatLab academic license is long over, so I ported all the code to R. The code is available in the repository . Also at my disposal was the code from the archive of the tsne R-package, took from there a couple of ideas.
For experiments it is proposed to use the following parameters:
Number of iterations: 1000;
Perplexia: 40;
Early hypergrowth: x4 for the first 50 iterations;
Moment α: 0.5 for the first 250 iterations, 0.8 for the remaining 750;
Learning rate η: originally 100 (in the original code - 500) and changes after each iteration in accordance with the scheme described by Robert Jacobs in 1988 (ref. 3).
The algorithm can be divided into three logical parts:
- Calculation of perplexion and Gaussian kernel for the vector of current values of sigma (or rather gamma, I used the variable, inverse of the square of sigma)
- Calculation of pairwise similarity p ij in a multidimensional space using a binary search for a given perplexion
- Calculate pairwise similarity for display space, loss function, and gradient
I will illustrate only the most important constructions. First of all, it is necessary to calculate the matrix of squares of the Euclidean distance for the initial data set. For this, it is better to use the rdist () function from the fields package. It works many times faster than the popular dist () from the basic stats package. Perhaps this is due to the fact that it is optimized for the Euclidean distance. Next, you need to initialize the display space. This can be done with the help of rnorm () with a zero mat. expectation and standard deviation 1e-4.
The calculation of the logarithm of perplexia and the Gaussian core is as follows:
P <- exp(-Di * gamma) # kernel calc sumP <- sum(P) PP <- log(sumP) + gamma * sum(Di * P) / sumP The last expression is obtained if formula (1) for p j | i is substituted with formula (2) for perplexion. Let n be the number of points in the source data. Di is the vector of length n-1, with squares of pairwise distances for the line of the original data. It turns out with the help of the construction Di <- D [i, -i] , where D is the matrix of squares of distances nxn, and if i = 1, then Di is the first row of the matrix D without the first column. The kernel, P is a vector, the length is n-1, and the logarithm of perplexion is a real number (due to the sum of elementary products). The original code uses the natural logarithm, I decided to do the same.
For the search for gamma, there are the following restrictions - the number of attempts (divisions) is no more than 50, the threshold difference between the logarithms of a given and the calculated perplexion is 1e-5. One iteration of the binary search is as follows:
if (perpDiff > 0){ gammamin = gamma[i] if (is.infinite(gammamax)) gamma[i] = gamma[i] * 2 else gamma[i] = (gamma[i] + gammamax)/2 } else{ gammamax = gamma[i] if (is.infinite(gammamin)) gamma[i] = gamma[i]/ 2 else gamma[i] = ( gamma[i] + gammamin) / 2 } gammamin and gammamax are initially set to - and + Inf .
The loss function is calculated as the sum of the rows of the elementwise product of two nxn matrices:
cost = sum(apply(P * log(P/Q),1,sum)) P is a symmetric version of the joint probability for a multidimensional space, calculated as P = .5 * (P + t (P)) from the conditional pairwise probability, t is the matrix transposition operator. Q - joint probability for the display space:
num = 1/(1 + (rdist(Y))^2) diag(num)=0 # Set diagonal to zero Q = num / sum(num) # Normalize to get probabilities Y is the initialized matrix of points nx 2 for the two-dimensional mapping space. Q is obtained by the nxn matrix by using rdist () .
The gradient is calculated in vectorized form for all Yi at once:
L = (P - Q) * num; grads = 4 * (diag(apply(L, 1, sum)) - L) %*% Y Here, grads is a matrix, the size of nx 2, which is formed by the matrix product. The construction in parentheses is an nxn matrix, on the main diagonal of which are row-by-line sums of the matrix L, and all other elements are taken with a minus sign. The matrix product allows us to multiply by the difference Y i and Y j and immediately calculate the sums of j (formula 4). True gradient is obtained opposite sign.
To search for optimal Y values, something similar to the delta-bar-delta heuristics is used. Its meaning is to adaptively change the step of learning. If the gradient does not change its sign at the next iteration, the step increases linearly (0.2 is added to the gain), if the sign changes, it decreases exponentially (the coefficient is multiplied by 0.8). Given that the gradient we have is the opposite sign:
gains = (gains + .2) * abs(sign(grads) != sign(incs)) + gains * .8 * abs(sign(grads) == sign(incs)) gains[gains < min_gain] = min_gain incs = momentum * incs - gains * epsilon * grads Y = Y + incs Experiments
I could not try to repeat the experiment described in the article (link 1). The idea of this experiment is to visualize the cluster structure for a set of MNIST images. One part of this set contains 60000 images of handwritten numbers from 0 to 9, 28x28 pixels. The data set can be downloaded from the site of the neuron network guru, Jan Lekun.
With loading in R it is necessary to tinker, but the readBin function () which allows to read (and write) the binary data helps. 20 random numbers:

As in the original experiment, I did not use the entire set, but only 6000 images selected randomly using the sample () function. 1000 iterations took a little less than one and a half hours on x64 c Intel Core i7 2.4 GHz. Result on the picture:

Colors are set using labels, MNIST is a marked set of data. The result can be significantly improved. As the authors advise, for the initial set of points, the main component analysis (PCA) should be done and the first 30 should be selected:

There are several PCA implementations for R. The simplest version is in two lines:
pca <- prcomp(X) X <- pca$x[,1:30] The speed of the algorithm is proportional to the square of the number of points. If this amount is reduced, the result will not be as obvious, but quite acceptable. Let's say 2000 points are processed in just 9 minutes.
The t-SNE technique would probably not be so popular if it were not for the ability to visualize the distributed representation of words. In this experiment, I used a relatively small model (about 900 words and a 300-dimensional feature space), trained with the help of word2vec .

Here the size is bigger. A three-dimensional display space is used, the third dimension is represented by color. Words can be considered close if they are located side by side and have the same shade.
It turns out that with a distributed representation of words prepared on real data, everything is not so simple. There are two problems: as a rule, a very large number of clusters and significant differences in their size. For visualization, you can make a random sample, but the result will most likely not be representative. The authors explain this with the following example: If A, B and C are equidistant points in multidimensional space, but there are points between A and B and there is no point between B and C, the algorithm is more likely to combine A and B into one cluster than B and C.
But it so happens that it is visibility that is important, not the fullness of the picture. Then, instead of a random sample of points, you can try to select interesting clusters. Clustering is built into the original word2vec, besides you can use k-means. Perhaps this option does not seem quite "fair", but, in my opinion, has the right to exist. Sampling data for a distributed representation of words from fifteen clusters does not look so confusing:

For large data sets, there is a special implementation of t-SNE, in which the nearest-neighbor trees and the random walk method are used to calculate the similarity in multidimensional space (described in article 1). In practice, you can use the Rtsne package, a wrapper for the C ++ implementation of the Barnes-Hut-SNE. Rtsne can process all 60000 MNIST images in less than an hour. Details can be found in publication 6.
I have not experimented with Rtsne yet, but I have tested tsne (MatLab port of R code). The visualization is much worse than my version. Looking into the package archive, I discovered two things: First, when calculating the Gaussian core, the distance is used without a square, and second, the matrix product is used in the expression for perplexion. In my version and in the code for MatLab, it is elementwise. It is strange that generally turned out visible clusters. I explain this by the “survivability” of the algorithm, but I admit that I did not fully understand something. I would be happy to comment and wish you all impressive multidimensional visualizations.
Formulas for this article are prepared using the online formula editor LATEX .
References:
- LJP van der Maaten and GE Hinton. Visualizing High-Dimensional Data Using t-SNE. Journal of Machine Learning Research 9 (Nov): 2579-2605, 2008. PDF
- GE Hinton and ST Roweis. Stochastic Neighbor Embedding. In Advances in Neural Information. Processing Systems, volume 15, pages 833–840, Cambridge, MA, USA, 2002. The MIT Press. PDF
- RA Jacobs. Increased rates of convergence through learning rate adaptation. Neural Networks, 1: 295–307, 1988. PDF
- Experiments with t-SNE in Python: Algorithm t-SNE. Illustrated introductory course (translation of the original article on O'Reilly ). datareview.info/article/algoritm-t-sne-illyustrirovannyiy-vvodnyiy-kurs
- Rtsne versus tsne: www.codeproject.com/Tips/788739/Visualization-of-High-Dimensional-Data-using-t-SNE A set of data is also available for experiments with a distributed representation of words.
- LJP van der Maaten. Accelerating t-SNE using Tree-Based Algorithms. Journal of Machine Learning Research 15 (Oct): 3221-3245, 2014. PDF
Source: https://habr.com/ru/post/267041/
All Articles