Data structures Informal guide

Of course, you can be a successful programmer without sacred knowledge of data structures, but they are absolutely indispensable in some applications. For example, when you need to calculate the shortest path between two points on a map, or find a name in a phone book containing, say, a million entries. Not to mention the fact that data structures are constantly used in sports programming. Consider some of them in more detail.

Turn

So say hello to Lupi!





')

Lupi loves playing hockey with his family. And by “play,” I mean:







When the turtles fly into the gate, they are thrown to the top of the pile. Notice, the first bug added to the pile leaves it first. This is called the Queue . Just as in those queues that we see in everyday life, the first element added to the list leaves it first. Another structure called FIFO (First In First Out).



What about insert and delete operations?

q = [] def insert(elem): q.append(elem) #     print q def delete(): q.pop(0) #     print q 

Stack

After such a fun hockey game, Lupi makes pancakes for everyone. She puts them in one pile.







When all the pancakes are ready, Lupi serves them to the whole family, one by one.







Note that the first pancake she made will be served last. This is called Stack . The last item added to the list will be the first to leave. This data structure is also called LIFO (Last In First Out).



Adding and removing items?

 s = [] def push(elem): #    -  s.append(elem) print s def customPop(): #    -  s.pop(len(s)-1) print s 

A pile

Have you ever seen a density tower?







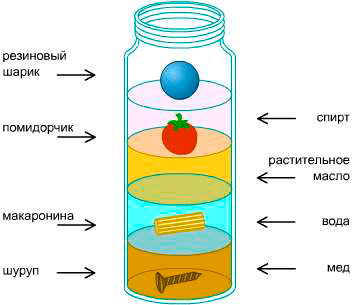
All elements from top to bottom are located in their places, according to their density. What happens if you throw a new object inside?







It will take place, depending on its density.



This is how the Heap works.







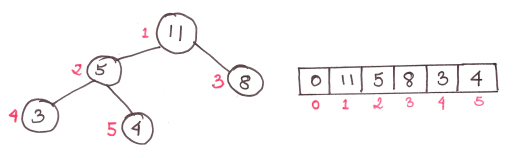
A pile is a binary tree. This means that each parent element has two children. And although we call this data structure a heap, but it is expressed through a regular array.

Also, the heap always has the height logn, where n is the number of elements



The figure shows a heap of max-heap type, based on the following rule: children are smaller than the parent. There are also min-heap heaps, where children are always larger than the parent.



Some simple functions for working with heaps:

 global heap global currSize def parent(i): #    i-  return i/2 def left(i): #     i- return 2*i def right(i): #     i- return (2*i + 1) 

Add item to existing heap

To begin with, we add an element to the bottom of the heap, i.e. at the end of the array. Then we swap it with the parent until it fits into place.







Algorithm:

1. Add an item to the bottom of the heap.
2. Compare the added item with the parent; if the order is correct, we stop.
3. If not, swap the elements and return to the previous item.

Code:

 def swap(a, b): #    a     b temp = heap[a] heap[a] = heap[b] heap[b] = temp def insert(elem): global currSize index = len(heap) heap.append(elem) currSize += 1 par = parent(index) flag = 0 while flag != 1: if index == 1: #    flag = 1 elif heap[par] > elem: #        -      flag = 1 else: #      swap(par, index) index = par par = parent(index) print heap 

The maximum number of passes of the while loop is equal to the tree height, or logn, therefore, the complexity of the algorithm is O (logn).



Retrieving Maximum Heap Element

The first item in the heap is always the maximum, so we just remove it (remembering beforehand) and replace it with the lowest one. Then we will bring a bunch in the correct order using the function:

 maxHeapify(). 

Algorithm:

1. Replace the root element of the lowest.
2. Compare new root element with children. If they are in the right order - stop.
3. If not, replace the root element with one of the children (smaller for min-heap, larger for max-heap), and repeat step 2.

Code:

 def extractMax(): global currSize if currSize != 0: maxElem = heap[1] heap[1] = heap[currSize] #   -  heap.pop(currSize) #   currSize -= 1 #   maxHeapify(1) return maxElem def maxHeapify(index): global currSize lar = index l = left(index) r = right(index) #,     ;     -   if l <= currSize and heap[l] > heap[lar]: lar = l if r <= currSize and heap[r] > heap[lar]: lar = r if lar != index: swap(index, lar) maxHeapify(lar) 

And again, the maximum number of calls to the maxHeapify function is equal to the height of the tree, or logn, which means the complexity of the algorithm is O (logn).



We make a bunch of any random array

OK, there are two ways to do this. The first is to insert each element into the heap one by one. It is simple, but completely ineffective. The complexity of the algorithm in this case will be O (nlogn), since O (logn) function will be executed n times.



A more efficient way is to use the maxHeapify function for sub-heap , from (currSize / 2) to the first element.



The complexity is O (n), and the proof of this statement, unfortunately, is beyond the scope of this article. Just understand that the elements in the heap part from currSize / 2 to currSize have no descendants, and most of the sub-heaps formed in this way will be less than logn.



Code:

 def buildHeap(): global currSize for i in range(currSize/2, 0, -1): #   range() -  ,     . print heap maxHeapify(i) currSize = len(heap)-1 

Indeed, why is this all?



Heaps are needed to implement a special type of sorting, called, oddly, “ heap sorting ”. Unlike the less effective “sorting by inserts” and “bubble sorting”, with their terrible complexity in O (n ² ), “heap sorting” has complexity O (nlogn).



Realization of indecency is simple. Just continue to consistently extract the maximum (root) element from the heap, and write it into an array until the heap is empty.



Code:

 def heapSort(): for i in range(1, len(heap)): print heap heap.insert(len(heap)-i, extractMax()) #      currSize = len(heap)-1 

To summarize all of the above, I wrote a few lines of code containing functions for working with the heap, and for OOP fans, I designed everything as a class .



Easy, isn't it? And here, celebrating Lupi!

Hash

Lupi wants to teach his kids to distinguish shapes and colors. For this, she brought home a huge number of colorful figures.







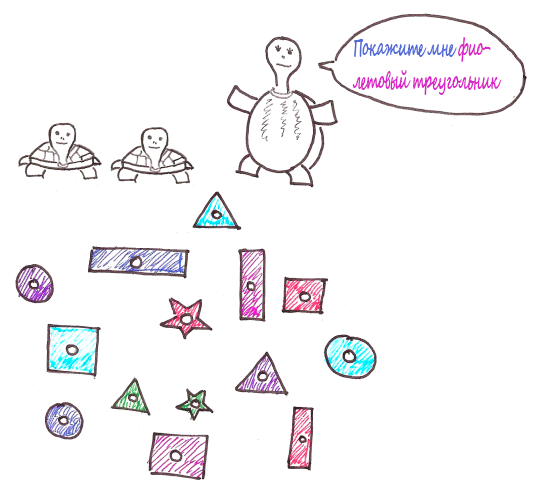
After a while, the turtles are completely confused.







So she took out another toy to simplify the process a bit.







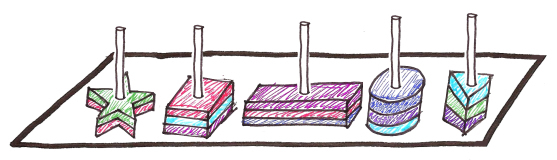
It has become much easier, because the turtles already knew that the figures were sorted according to shape. And what if we mark each pillar?







The turtles now need to check the column with a certain number, and choose from a much smaller number of figures. And if we also have a separate pillar for each combination of form and color?



Suppose the column number is calculated as follows:



Fio summer tri square

f + and + o + t + p + e = 22 + 10 + 16 + 20 + 18 + 6 = pillar 92



Red rectangle

+ + + + + = 12 + 18 + 1 + 17 + 18 + 33 = Column 99



etc.



We know that 6 * 33 = 198 possible combinations, so we need 198 pillars.



Let's call this formula for calculating the column number - Hash function .



Code:

 def hashFunc(piece): words = piece.split(" ") #    colour = words[0] shape = words[1] poleNum = 0 for i in range(0, 3): poleNum += ord(colour[i]) - 96 poleNum += ord(shape[i]) - 96 return poleNum 

( Cyrillic is a bit more complicated, but I left it for simplicity . - comment. per. )



Now, if we need to find out where the pink square is stored, we can calculate:

 hashFunc(' ')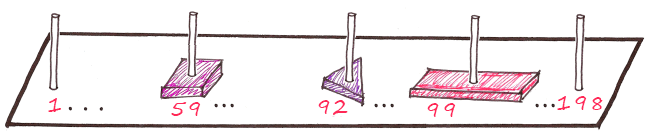 

This is an example of a hash table, where the location of the elements is determined by the hash function.

With this approach, the time spent searching for any item does not depend on the number of items, i.e. O (1). In other words, the search time in the hash table is a constant value.



Ok, but let's say we are looking for a “cartographic rectangle” (if, of course, the color “caramel” exists).

 hashFunc(' ') 

will return us 99, which is the same as the number for the red rectangle. This is called a " collision ". To resolve conflicts, we use the “ Chain method ”, meaning that each column stores a list in which we look for the record we need.



Therefore, we simply put the caramel rectangle on red, and choose one of them when the hash function points to this pillar.



The key to a good hash table is to choose a suitable hash function. Undoubtedly, this is the most important thing in creating a hash table, and people spend an enormous amount of time developing quality hash functions.

In good tables, no single position contains more than 2-3 elements, otherwise, hashing does not work well, and the hash function needs to be changed.







Once again, the search is not dependent on the number of elements! We can use hash tables for everything that has gigantic sizes.



Hash tables are also used to search for strings and substrings in large chunks of text, using the Rabin-Karp algorithm or the Knut-Morris-Pratt algorithm, which is useful, for example, for determining plagiarism in scientific papers.







On this, I think you can finish. In the future, I plan to consider more complex data structures, such as the Fibonacci heap and the segment tree . I hope this informal guide turned out to be interesting and useful.



Translated to Habr by a programmer locked in the attic .