Algorithm for parsing arithmetic expressions

General information

The article describes one of the possible algorithms for the software implementation of the parser of arithmetic expressions, with the possibility of subsequent calculation of their values.

A parser is a program that analyzes an input arithmetic expression. Programs of this class are sometimes also called “recognizers”.

Parsing is the process of parsing the input arithmetic expression into simpler components.
')
The result of the parser is a formed tree of tokens. By lexemes, we mean fragments of an input arithmetic expression that are not subject to further splitting into component parts.

The description of the recognition algorithm is given without reference to any programming language. The article concludes with an example of implementing this algorithm in PHP. The implementation of the algorithm is possible in almost any programming language (even without OOP support).

Formulation of the problem

Suppose that the parser takes an arithmetic expression as an input, which is a regular string of the form: (x + 10.2) ^ 2 + 5 * yz . The input expression is correct in terms of the grammar of arithmetic expressions:

• The number of opening brackets is equal to the number of closing brackets.
• The integer part of the number is separated from the fractional by a point.
• The string contains only valid characters: the digits 0 ... 9 , the operators + - * / ^ , the brackets, the point and the parameters x, y, z .

The parser must build a tree of tokens suitable for calculating the numerical value of the input expression. The values ​​of the parameters will be passed to the method that implements the calculation of the numerical value.

For each specific expression, the tree of objects is built once. Then, using the obtained tree of objects, we calculate the final value of the output expression taking into account the values ​​of the parameters. You can repeat the calculations unlimited number of times.

The algorithm should allow processing of input expressions of unlimited length (within reasonable limits) without restrictions on the level of nesting of parentheses.

Lexical analysis of the input expression

Before proceeding directly to parsing the input expression, it is advisable to remove insignificant characters (such as a space, etc.) and form solid lexemes. This procedure is not mandatory within the framework of the algorithm, however, it allows to significantly simplify the understanding of the algorithm itself and its software implementation.

For example, let us return to the consideration of the line of the arithmetic expression given above: (x + 10.2) ^ 2 + 5 * yz . In the process of lexical analysis, the specified string will be converted into an array of strings of the following structure: [0] => ”(”, [1] => ”x”, [2] => ”+”, [3] => ”10.2”, [4] => ”)”, [5] => ”^”, [6] => ”2”, [7] => ”+”, [8] => ”5”, [9] => ”*”, [10] => ”y”, [11] => ”-”, [12] => ”z” .

Thus, a solid lexeme is either an operator (arithmetic operation), or an operand (a number consisting of one or several digits), or a parameter ( x, y, z ) or a bracket (as an element that changes the priority of performing arithmetic operations in ).

Token as an object

Each integral lexeme in the tree structure is described by an object. Any object "tree" has a set of properties (fields) and a specific behavior. We list the estimated set of data fields for each object that models the token:

1. Name field - defines the unique name of the object.
2. The lec field is an array of tokens, for storing information about that part of the input expression whose vertex is this node of the "tree" of objects.
3. Const field - if this object is a parameter, then the variable stores its name.
4. Var field - if this object is a number or a parameter, then the variable stores its value.

The behavior of each object is characterized by a combination of methods. For this case, one method is enough, for example: calc (). If an object describes the behavior of an operand (number) or parameter, then it is necessary that it return this number or parameter value. If an object describes a token that is one of the operators (arithmetic operations), then the method should return the result of applying this operator to two numbers.

All objects of a tree structure may belong to the same class; it is enough just to override one method when creating an object. Or, alternatively, we can describe an abstract class with one abstract function calc () . Next, for each type of lexeme, we describe our class, which inherits the abstract class and determines the specific behavior of the calc () method. In the example of the software implementation, the last method is chosen, which requires a significantly smaller amount of code.

Some fields may remain blank - it depends on which lexeme is modeled by this particular object.

Token as a node of the tree structure

The configuration of objects that simulate lexemes is in general clear. But this raises the question of how to form a tree structure from these objects?

This problem is quite typical for software projects. The essence of the solution can be obtained from the design pattern with the name: "Linker". Blind copying of all the subtleties of this design pattern (pattern) is not included in our plans, so we are trying to highlight the most important and necessary for a particular case.

To arrange objects in the tree structure, add three more fields to each object:

1. The childrenLeft field is the left "heir" of this object.
2. The childrenRight field is the right "heir" of this object.
3. The parent field is the “parent” of this object.

Hereinafter, the terms “parent” and “heir” are used without being tied to one of the key OOP principles, and in the context of indicating the relative location of other objects relative to a given one in a formed tree structure.
To clarify the above, we present an image of a tree structure for the expression “(x + 10.2) ^ 2 + 5 * yz”, indicating the values ​​of all fields of the objects.



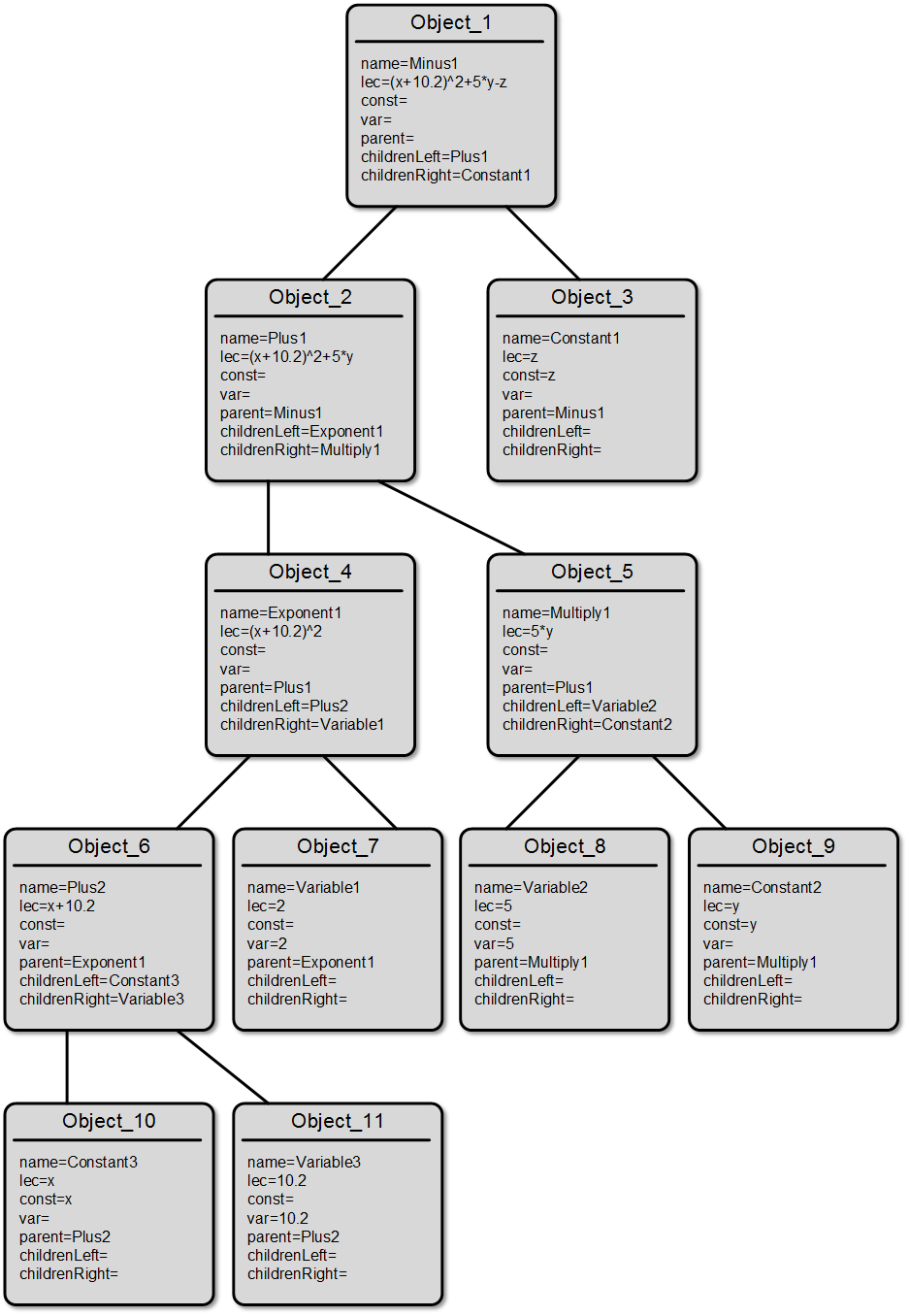
From the above scheme, it becomes extremely clear why each node can have only two “heirs”, or not have them at all.

The resulting structure of objects is quite acceptable for calculating the values ​​of arithmetic expressions by calling the calc () method of the highest on the object scheme.

Search for the inflection point of an arithmetic expression

The “inflection point” of an arithmetic expression is understood to be one of the elements of the array of tokens, which is an operator (an arithmetic operation) and has a maximum priority value relative to other operators.

To enter the ability to estimate the priority values ​​of arithmetic operations in the program, it is enough to define an array with the structure: [+] => 3, [-] => 3, [*] => 2, [/] => 2, [^] => 1 .

If the priority value is maximum for several operators, the last of them should be chosen, this will allow forming a tree structure that correctly calculates the numerical values.

Next, in the array of lexemes, the elements standing to the left of the “inflection point” are highlighted and are recorded in the lec field of the object that is the left “heir”. The elements located to the right of the “inflection point” are entered into a similar field of the right “heir”. It should also be mentioned that when searching for the “inflection point” one should take into account the level of nesting of brackets in the array of whole lexemes.

Construction of a tree structure

In this section, we analyze in detail the sequence of formation of the “tree” of objects within the framework of the proposed algorithm.
Consider the procedure for building the first three objects of the "tree", including the root object and its two "heirs". Having received at the input an array of solid tokens of the entire arithmetic expression, we find in it the “inflection point”. Let me remind you that this is always an operator (arithmetic action). The value of the “inflection point” found makes it possible to uniquely determine the class of an object located at the top of the structure. Next, we divide the array of tokens into two parts, as described above. In each of both parts, we also find points of "inflection", which indicate the class of objects of the left and right "heirs." Now you can create all three objects and specify the links between them. Finally, the objects are placed into the arNode array for subsequent actions on them.

For our input expression: (x + 10.2) ^ 2 + 5 * yz, the described procedure is as follows. The definition of the "inflection point" includes two operators: "+" (between the numbers "2" and "5") and "-". Select the last operator in the list: "-". The value of this operator allows you to select the desired class of the root object and its name. In particular, a Minus class object with the name Minus1 is formed . After dividing the initial array of lexemes into two parts, we obtain two arrays of elements: (x + 10.2) ^ 2 + 5 * y and z . For the first lexeme, the inflection point is “+”, and the second consists of only one element z . This means that as the "heirs" of the root object, you should create objects of the classes Plus and Constant with the names Plus1 and Constant1, respectively. It remains to fill the fields of the newly created objects: childrenLeft , childrenRight and parent to form a tree structure and add objects to the arNode array.

Further formation of the "tree" is very similar to the procedure for creating the first three, but has its own subtleties. In the arNode array, we simply search the array elements for an object with a lec field containing more than one element in the array and at the same time with the empty childrenLeft and childrenRight fields. We read the value of the lec field for the selected object, divide it into two parts at the “inflection point”. Next, we find the “inflection points” of the resulting two parts and form two heir objects for the selected object, in accordance with the logic outlined above. Do not forget to form links between objects and add the objects themselves to the arNode array.

We repeat the specified sequence of actions until none of the objects of the tree structure corresponds to the specified conditions. Now we can assume that the "tree" for our input expression is built and ready to calculate the values.

Calculating values

The process of calculating the values ​​of the input arithmetic expression becomes very clear when viewing the listing of the software implementation of the algorithm. Let us dwell on some significant points.

The calculation occurs after calling the calc () method of the object of the class Main . The program provides the ability to use no more than three parameters when calling this method: x , y , z . It is easy to change this number to meet the needs of a specific application of the described algorithm.

Previously, the method searches the array for objects describing the parameter tokens, then in the var fields of the found objects, the numeric values ​​specified when calling the calc () method are entered. Now you can start searching in the arNode array of an object with an empty parent field (this will be the root object of the tree structure) and call its calc () method. The method returns the value of an arithmetic expression.

Sample software implementation

Listing of software implementation decided to lay out entirely. This allows you to copy the entire program when you need to experiment with it or refine it.

<!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <title></title> </head> <body> <?php class Main { //    var $arNode = Array(); //      public function calc($x, $y, $z){ if($x){ foreach ($this->arNode as $obj){ if($obj->const == "x"){ $obj->var = $x; break; } } } if($y){ foreach ($this->arNode as $obj){ if($obj->const == "y"){ $obj->var = $y; break; } } } if($z){ foreach ($this->arNode as $obj){ if($obj->const == "z"){ $obj->var = $z; break; } } } foreach ($this->arNode as $obj){ if(!$obj->parent){ return $obj->calc(); } } } //     public function builder ($str) { //    $arNode = Array(); //      function parse ($str){ //      $str = mb_strtolower($str, 'UTF-8'); $str = str_replace(" ", "", $str); $n = mb_strlen($str, 'UTF-8'); $arStr = preg_split('/(?!^)(?=.)/u', $str); echo '<pre>'; echo print_r($arStr); echo '</pre>'; //       $j=0; $accum = $arStr[0]; for($i=1; $i<$n+1; ++$i){ if ($i==$n+1){ $arLec[$j] = $accum; break; } if($accum=="-" && $i==1){ if(preg_match("/\d/", $arStr[$i])){ $accum = $accum.$arStr[$i]; } if($arStr[$i]=="("){ $arLec[$j] = "0"; $arLec[++$j] = "-"; ++$j; $accum = $arStr[$i]; } continue; } if($accum=="-" && $arLec[$j-1]=="("){ $accum = $accum.$arStr[$i]; continue; } if (preg_match("/^[\d.]/", $accum) && preg_match("/^[\d.]/", $arStr[$i])){ $accum = $accum.$arStr[$i]; }else{ $arLec[$j] = $accum; ++$j; $accum = $arStr[$i]; } } /* $j = 0; if($arStr[0]=="-"){ $accum = $arStr[0]; }else{ $accum = $arStr[0]; } for ($i=1; $i<$n+1; ++$i){ if ($i==$n+1){ $arLec[$j] = $accum; continue; } if (preg_match("/^[\d.]/", $accum)&&preg_match("/^[\d.]/", $arStr[$i])){ $accum = $accum.$arStr[$i]; }else{ $arLec[$j] = $accum; ++$j; $accum = $arStr[$i]; } } * */ echo '<pre>'; echo print_r($arLec); echo '</pre>'; return $arLec; } //    function objBuilder($point){ static $arNumNode = Array( "addition" => 1, "subtraction" => 1, "exponentiation" =>1, "multiplication" => 1, "division" => 1, "number" => 1, "constant" => 1); switch ($point){ case "+": $name = "Plus".$arNumNode["addition"]; $node = new Plus($name); ++$arNumNode["addition"]; break; case "-": $name = "Minus".$arNumNode["subtraction"]; $node = new Minus($name); ++$arNumNode["subtraction"]; break; case "*": $name = "Multiply".$arNumNode["multiplication"]; $node = new Multiply($name); ++$arNumNode["multiplication"]; break; case "/": $name = "Fission".$arNumNode["division"]; $node = new Fission($name); ++$arNumNode["division"]; break; case "^": $name = "Exponent".$arNumNode["exponentiation"]; $node = new Exponent($name); ++$arNumNode["exponentiation"]; break; case "x": $name = "Constant".$arNumNode["constant"]; $node = new Constant($name); $node->const = "x"; $node->var = 0; ++$arNumNode["constant"]; break; case "y": $name = "Constant".$arNumNode["constant"]; $node = new Constant($name); $node->const = "y"; $node->var = 0; ++$arNumNode["constant"]; break; case "z": $name = "Constant".$arNumNode["constant"]; $node = new Constant($name); $node->const = "z"; $node->var = 0; ++$arNumNode["constant"]; break; default: $name = "Variable".$arNumNode["number"]; $node = new Variable($name); $node->var = $point; ++$arNumNode["number"]; } return $node; } //     function trioBuilder($topLec, $leftLec, $rightLec, $topP, $leftP, $rightP, $topObj){ //   if(!$topObj){ $topTrio = objBuilder($topP); $topTrio->lec = $topLec; } else { $topTrio = $topObj; } //    $leftTrio = objBuilder($leftP); $leftTrio->lec = $leftLec; //    $rightTrio = objBuilder($rightP); $rightTrio->lec = $rightLec; //     $topTrio->childrenLeft = $leftTrio; $topTrio->childrenRight = $rightTrio; $leftTrio->parent = $topTrio; $rightTrio->parent = $topTrio; if(!$topObj){ $trio = Array($topTrio, $leftTrio, $rightTrio); return $trio; } else { $duo = Array($leftTrio, $rightTrio); return $duo; } } //      function stopBuild($arNode){ foreach ($arNode as $obj){ if($obj->lec[1] && !$obj->childrenLeft && !$obj->childrenRight){ return FALSE; } } return TRUE; } //      function searchObj($arNode){ foreach ($arNode as $obj){ if($obj->lec[1] && !$obj->childrenLeft && !$obj->childrenRight){ return $obj; } } } //     function inflPoint($lec){ $infl=0; $max=0; static $br = 0; static $arPrioritet = Array( "+" => 3, "-" => 3, "*" => 2, "/" => 2, "^" => 1); foreach ($lec as $key=>$value){ if(preg_match("/^[\d.]/", $value)){ continue; } if($value=="("){ ++$br; continue; } if($value==")"){ --$br; continue; } if($arPrioritet[$value]-3*$br >= $max){ $max=$arPrioritet[$value]-3*$br; $infl=$key; } } return $infl; } $arLec = parse($str); //    $topN = inflPoint($arLec); $topP = $arLec[$topN]; $leftLec = array_slice($arLec, 0, $topN); if($leftLec[0]=="(" && $leftLec[count($leftLec)-1]==")"){ array_shift($leftLec); array_pop($leftLec); } $rightLec = array_slice($arLec, $topN+1); if($rightLec[0]=="(" && $rightLec[count($rightLec)-1]==")"){ array_shift($rightLec); array_pop($rightLec); } $leftN = inflPoint($leftLec); $leftP = $leftLec[$leftN]; $rightN = inflPoint($rightLec); $rightP = $rightLec[$rightN]; $trio = trioBuilder($arLec, $leftLec, $rightLec, $topP, $leftP, $rightP, NULL); $arNode = $trio; //     while (!stopBuild($arNode)){ $topTrio = searchObj($arNode); $arLec = $topTrio->lec; $topN = inflPoint($arLec); $leftLec = array_slice($arLec, 0, $topN); if($leftLec[0]=="(" && $leftLec[count($leftLec)-1]==")"){ array_shift($leftLec); array_pop($leftLec); } $rightLec = array_slice($arLec, $topN+1); if($rightLec[0]=="(" && $rightLec[count($rightLec)-1]==")"){ array_shift($rightLec); array_pop($rightLec); } $leftN = inflPoint($leftLec); $leftP = $leftLec[$leftN]; $rightN = inflPoint($rightLec); $rightP = $rightLec[$rightN]; $duo = trioBuilder(NULL, $leftLec, $rightLec, NULL, $leftP, $rightP, $topTrio); $arNode = array_merge($arNode, $duo); } $this->arNode = $arNode; } } abstract class Term { public $name; public $childrenLeft; public $childrenRight; public $parent; public $lec; public $const; public $var; public function __construct($name) { $this->name = $name; } abstract function calc(); } class Plus extends Term { public function calc() { return $this->childrenLeft->calc()+$this->childrenRight->calc(); } } class Minus extends Term { public function calc() { return $this->childrenLeft->calc()-$this->childrenRight->calc(); } } class Multiply extends Term { public function calc() { return $this->childrenLeft->calc()*$this->childrenRight->calc(); } } class Fission extends Term { public function calc() { return $this->childrenLeft->calc()/$this->childrenRight->calc(); } } class Exponent extends Term { public function calc() { return pow ($this->childrenLeft->calc(), $this->childrenRight->calc()); } } class Constant extends Term { public function calc() { return $this->var; } } class Variable extends Term { public function calc() { return $this->var; } } //     $str = "(x+10.2)^2+5*yz"; $x = 2; $y = 1; $z = 3; $parse = new Main(); //    $parse->builder($str); //echo '<pre>'; //echo print_r($parse->arNode); //echo '</pre>'; echo $str." = ".$parse->calc($x, $y, $z); echo " : x=".$x."; y=".$y."; z=".$z; ?> </body> </html> 

If you remove the comments from the three consecutive echo statements at the end of the program, you can analyze the correctness of the formation of the tree structure and see the field values ​​of all objects.

Conclusion

I tried to describe the algorithm in as much detail as possible, but if you have any questions, write, I will try to answer everyone. I would also be grateful for reports of errors and inaccuracies in the text.