A brief history of the evolution of proof-of-work in cryptocurrencies. Part 1
I bring to your attention a translation of the article “The Proof-of-the-Work in Cryptocurrencies: Brief History. Part 1 » Ray Patterson (Ray Patterson) from the site Bytecoin.org .

The concept of proof-of-work - “proof of (completed) work” - first appeared in “Pricing via Processing or Combatting Junk Mail”in 16 before the birth of Bitcoin in 1993. And although there is no such term in this article (there will be after 6 years), we will call it that way (PoW for short). What idea did Cynthia Dwork and Moni Naor suggest in their work?
“To get access to a shared resource, the user must calculate a certain function: quite complicated, but feasible; so you can protect the resource from abuse "
')
To draw an analogy, the Fish Inspectorate requires Jeremy Wade to work a little to gain access to the local pond — for example, plant several trees and send photos of seedlings. At the same time, Jeremy should be able to cope with it in a reasonable time: before all the fish are poisoned by substances released into the environment. But, on the other hand, the work should not be elementary, otherwise the crowds of fishermen will quickly devastate the entire pond.
In the digital world, to come up with an example of this kind of work is actually not so trivial.
The server can, for example, prompt the user to multiply two random long numbers and then check the result. The problem is obvious: the check is not much faster than the work itself, i.e. the server simply cannot handle a large stream of clients.
Next attempt: the server comes up with two long simple numbers, multiplies them and reports the result to the user. The latter must perform a factorization, it is already more difficult. There are nuances here, but in general, the scheme has become better: the ratio “time of work / time of verification” has greatly increased. This is the main requirement formulated in the article:
"The calculation of the function at a given input should be much more difficult than checking the result"
In addition, it was required that the function not be depreciable (read - not parallelized), i.e. so that the time to solve several tasks is proportional to their number (If Jeremy wants to get a double quota for fishing, then you need to work twice as long: yesterday's or other people's photos will not work).
As an example of such functions, (among others) the calculation of the square root modulo a prime number P was proposed: here we have log (P) multiplications per solution and only one multiplication for testing). The input value can be issued as a server (generate x, issue x ^ 2), or be selected independently: select x, find sqrt (hash (x)). In the latter case, a small file is needed: not every element in Z_p is a square. But this is the little things.
During the following years, other work appeared on the proof-of-work keywords. Among them are two:
It would be wrong to say that Satoshi was the first to invent PoW for electronic money. The idea called “reusable proof-of-work” was vital in crypto-anarchist circles (and even partially implemented), but did not gain popularity in its original form.
The concept of RPoW from Hal Finney suggested that the “tokens-proofs” themselves would be an independent value (coins), while in Bitcoin the PoW mechanism was used as a means of achieving a distributed consensus (consensus about which version of the blockchain to be considered correct). And this was the key idea of Bitcoin, which “shot”.
The idea of Hashcash was chosen as the proof-of-work scheme, and the calculated function was SHA-256, the most popular hash function at the time (2008). Most likely, it was the simplicity of Hashcash and the “standard” of SHA-256 that turned out to be the decisive factors. Satoshi added a mechanism of varying complexity to Hashcash (reduce-increase N — the required number of zeros — depending on the total capacity of the participants), and this would seem to provide everyone with a cloudless, decentralized future. But then something happened: GPU, FPGA, ASIC, and even cloud-based decentralized mining. You can find a detailed history (in three volumes) of the development of mining in Bitcoin here .
There is no consensus about whether “Satoshi had foreseen” all this disgrace or not, but the fact is this: already in September 2011, the first cryptocurrency with a fundamentally different PoW function appeared: Tenebrix used scrypt instead of SHA-256 .
So, why, instead of such useful and important changes in the Bitcoin code, such as, for example, the total number of coins, the crucial element — the consensus algorithm — began to be changed? The reason is obvious: in 2011, GPU-farms were already working with might and main, pre-orders for FPGAs were being assembled, and ASICs were potentially looming - that is, the contribution of the usual CPU user was almost zero. But what is the reason?
You can, of course, explain everything with the usual resentment or the desire to “cut the dough”: before Tenebrix, there were already forks, and premina, and pump'n'dump. But the arguments of the supporters of the “ASIC-resistance” functions are quite reasonable:
Of course, every point can always be objected to, but I just want to show that when choosing a PoW function, it makes sense to think about its “ASIC security”. In fact, this aspect was implicitly mentioned in the very first article! It is precisely the non-depreciating function that can with a stretch be considered ASIC-protected.
Now there are some technical details on how the scrypt algorithm, which formed the basis of Tenebrix, and later on Litecoin (which, as you may know, became the second most popular cryptocurrency), works.
Strictly speaking, scrypt is not a cryptographic hash function, but a key generation function (KDF). Such algorithms are used for exactly where you thought: to get the secret key from some data (passphrase, random bits, etc.). Examples include PBKDF2 and bcrypt.
The main task of KDF is to make it difficult to generate the final key: not much, so that it can be used in applied tasks, but enough to prevent cases of malicious use (for example, enumerating passwords). The wording is very similar to something, isn't it? No wonder they met - like Zita and Gita - PoW and KDF.
The scrypt parameters for Tenebrix were chosen in such a way that the total amount of required memory would fit in 128 KB: so you can fit in the processor's L2 cache. And the default is 16 MB! The experiment turned out to be more than successful: CPU miners who were forgotten on the side of progress quickly got into the game. The vast majority of new forks have sprung from Litecoin, inheriting scrypt instead of SHA256.
Strangely enough, users were not embarrassed by the fact that the 128 KB parameters were completely in the teeth and video cards. The optimized GPU miner appeared a few months later and gave an average of a tenfold increase in efficiency. “But not 100 times as in Bitcoin!” They said, “But not 1000 times!” The increase in the ratio of GPU / CPU-capacities (displaced from Bitcoin by new ASICs) was not so sharp, probably because what was compensated for the forks boom: a new scrypt-cryptocurrency appeared almost once a week, putting off new capacities.
And yet, the understanding that scrypt is far from an ideal PoW function appeared even earlier than the announcement of scrypt-ASIC. The dizziness from successes passed, the cult of Satoshi subsided a bit, and ideas for new PoW candidates began to appear as after the rain.
“Cross and multiply: X11 and Co. algorithms!”
“Atavisms against rudiments: SHA3 or scrypt-jane?”
“Paradoxes of history: Momentum and birthday paradox”
“Where is the peak of evolution: in theoretical computer science or practical? CuckooCycle and CryptoNight »

Until the beginning of time
The concept of proof-of-work - “proof of (completed) work” - first appeared in “Pricing via Processing or Combatting Junk Mail”
“To get access to a shared resource, the user must calculate a certain function: quite complicated, but feasible; so you can protect the resource from abuse "
')
To draw an analogy, the Fish Inspectorate requires Jeremy Wade to work a little to gain access to the local pond — for example, plant several trees and send photos of seedlings. At the same time, Jeremy should be able to cope with it in a reasonable time: before all the fish are poisoned by substances released into the environment. But, on the other hand, the work should not be elementary, otherwise the crowds of fishermen will quickly devastate the entire pond.
In the digital world, to come up with an example of this kind of work is actually not so trivial.
The server can, for example, prompt the user to multiply two random long numbers and then check the result. The problem is obvious: the check is not much faster than the work itself, i.e. the server simply cannot handle a large stream of clients.
Next attempt: the server comes up with two long simple numbers, multiplies them and reports the result to the user. The latter must perform a factorization, it is already more difficult. There are nuances here, but in general, the scheme has become better: the ratio “time of work / time of verification” has greatly increased. This is the main requirement formulated in the article:
"The calculation of the function at a given input should be much more difficult than checking the result"
In addition, it was required that the function not be depreciable (read - not parallelized), i.e. so that the time to solve several tasks is proportional to their number (If Jeremy wants to get a double quota for fishing, then you need to work twice as long: yesterday's or other people's photos will not work).
As an example of such functions, (among others) the calculation of the square root modulo a prime number P was proposed: here we have log (P) multiplications per solution and only one multiplication for testing). The input value can be issued as a server (generate x, issue x ^ 2), or be selected independently: select x, find sqrt (hash (x)). In the latter case, a small file is needed: not every element in Z_p is a square. But this is the little things.
During the following years, other work appeared on the proof-of-work keywords. Among them are two:
- Hashcash project by Adam Beck , dedicated to the same anti-spam protection. The task was formulated as follows: “To find such a value of x that the SHA (x) hash would contain N higher zero bits”. That is, in fact, the work was reduced to hashing the same data (letters) with the enumerated part. Since a persistent, irreversible hash function is used, there is nothing better than iteration; and the average amount of work depends exponentially on N. A very simple scheme, yes?
- “Moderately hard, memory-bound functions” . The key word here is memory-bound. By the beginning of the zero, it became noticeable that the difference between low-end and high-end processors is too large for PoW-tasks to cut one size fits all. The algorithm proposed in the article was the first to use relatively large (megabytes) memory in the calculations. The bottleneck in such schemes was not the processor speed, but the delay in exchanging data with RAM or the amount of required memory, which varied in computers within narrower limits. One of these algorithms was scrypt , but more on that later.
Unicellular
It would be wrong to say that Satoshi was the first to invent PoW for electronic money. The idea called “reusable proof-of-work” was vital in crypto-anarchist circles (and even partially implemented), but did not gain popularity in its original form.
The concept of RPoW from Hal Finney suggested that the “tokens-proofs” themselves would be an independent value (coins), while in Bitcoin the PoW mechanism was used as a means of achieving a distributed consensus (consensus about which version of the blockchain to be considered correct). And this was the key idea of Bitcoin, which “shot”.
The idea of Hashcash was chosen as the proof-of-work scheme, and the calculated function was SHA-256, the most popular hash function at the time (2008). Most likely, it was the simplicity of Hashcash and the “standard” of SHA-256 that turned out to be the decisive factors. Satoshi added a mechanism of varying complexity to Hashcash (reduce-increase N — the required number of zeros — depending on the total capacity of the participants), and this would seem to provide everyone with a cloudless, decentralized future. But then something happened: GPU, FPGA, ASIC, and even cloud-based decentralized mining. You can find a detailed history (in three volumes) of the development of mining in Bitcoin here .
There is no consensus about whether “Satoshi had foreseen” all this disgrace or not, but the fact is this: already in September 2011, the first cryptocurrency with a fundamentally different PoW function appeared: Tenebrix used scrypt instead of SHA-256 .
Mutation
So, why, instead of such useful and important changes in the Bitcoin code, such as, for example, the total number of coins, the crucial element — the consensus algorithm — began to be changed? The reason is obvious: in 2011, GPU-farms were already working with might and main, pre-orders for FPGAs were being assembled, and ASICs were potentially looming - that is, the contribution of the usual CPU user was almost zero. But what is the reason?
You can, of course, explain everything with the usual resentment or the desire to “cut the dough”: before Tenebrix, there were already forks, and premina, and pump'n'dump. But the arguments of the supporters of the “ASIC-resistance” functions are quite reasonable:
- Popularization
Since each computer (in theory) gives approximately the same hashrate, more people will participate in mining, even in the background. Hundreds of millions of office machines, having slightly loaded their CPU, will contribute to the protection of the network, receive coins for this, which will then turn into circulation. - Decentralization.
There are even two aspects: first, iron producers. Most of the ASICs are produced in several factories in China, and units are also competent in manufacturing. Another thing is a general purpose PC. Secondly, the geographical location of the miners. If you do not take into account the pools, then the universal CPU-friendly algorithm has a larger area of distribution: anyone can afford to run the miner. - The high cost of attack 51%.
Of course, you can always design a special device that solves a specific task more efficiently (by time or by energy costs) than a regular PC. Another question: how much will it cost to reseach + development of such a device, what scale of production should be, for the whole project to be economically beneficial, etc.? It is believed that in any case it will be more expensive than in the current reality of Bitcoin. (This is not an absolute estimate of the cost of an attack: a relatively, roughly speaking, level of maturity of the entire network. So, say, a network with even the most superlative ASIC-proof algorithm can be cheaply attacked if it only mines two dozen machines. )
Of course, every point can always be objected to, but I just want to show that when choosing a PoW function, it makes sense to think about its “ASIC security”. In fact, this aspect was implicitly mentioned in the very first article! It is precisely the non-depreciating function that can with a stretch be considered ASIC-protected.
Now there are some technical details on how the scrypt algorithm, which formed the basis of Tenebrix, and later on Litecoin (which, as you may know, became the second most popular cryptocurrency), works.
Strictly speaking, scrypt is not a cryptographic hash function, but a key generation function (KDF). Such algorithms are used for exactly where you thought: to get the secret key from some data (passphrase, random bits, etc.). Examples include PBKDF2 and bcrypt.
The main task of KDF is to make it difficult to generate the final key: not much, so that it can be used in applied tasks, but enough to prevent cases of malicious use (for example, enumerating passwords). The wording is very similar to something, isn't it? No wonder they met - like Zita and Gita - PoW and KDF.
Scrypt work pattern
The first layer:
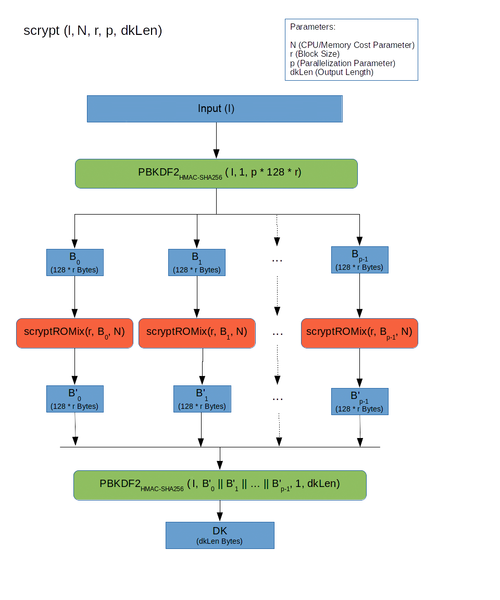
Note that here each of the p blocks can be processed separately. Those. scrypt in theory allows for parallelization (but by default, p = 1)
Second layer:

Here the most interesting thing happens. The larger the N value we choose, the more memory is required by the algorithm. And although at each step 2-3 we need only one element from the entire array, we cannot free up memory until step 5: after all, this element is chosen pseudo-randomly, depending on the last result! Thus, if the BlockMix function itself (see below) is executed quickly, latency becomes a bottleneck.
The third layer.

Salsa20 / 8 is used as a function of H. Yes, this is not a hash function, but a stream cipher. But for scrypt purposes, collision resistance is not required, but only a quick and pseudo-random result, so Salsa was very suitable. By default, scrypt suggests r = 8, but in the cryptocurrency they chose r = 1 (most likely, for speed). We will write about the consequences later.
Details regarding the choice of certain parameters in the algorithm can be found here .
- Input is passed through PBKDF2
- They are divided into p blocks, each processed by the SMix function,
- The result is glued together again and passed through PBKDF2.

Note that here each of the p blocks can be processed separately. Those. scrypt in theory allows for parallelization (but by default, p = 1)
Second layer:
- The input block by successively applying the pseudo-random function BlockMix expands to an array of N blocks.
- Block X, obtained from the last element, is interpreted as an integer j, and element Vj is read from the array
- X = BlockMix (X xor Vj)
- Steps 2-3 are repeated N times.
- The result is the current value of the X block.

Here the most interesting thing happens. The larger the N value we choose, the more memory is required by the algorithm. And although at each step 2-3 we need only one element from the entire array, we cannot free up memory until step 5: after all, this element is chosen pseudo-randomly, depending on the last result! Thus, if the BlockMix function itself (see below) is executed quickly, latency becomes a bottleneck.
The third layer.
- The input is divided into 2r blocks
- Each block is xor-is with the previous one and is hashed by the function H
- The result is given in the rearranged order.

Salsa20 / 8 is used as a function of H. Yes, this is not a hash function, but a stream cipher. But for scrypt purposes, collision resistance is not required, but only a quick and pseudo-random result, so Salsa was very suitable. By default, scrypt suggests r = 8, but in the cryptocurrency they chose r = 1 (most likely, for speed). We will write about the consequences later.
Details regarding the choice of certain parameters in the algorithm can be found here .
The scrypt parameters for Tenebrix were chosen in such a way that the total amount of required memory would fit in 128 KB: so you can fit in the processor's L2 cache. And the default is 16 MB! The experiment turned out to be more than successful: CPU miners who were forgotten on the side of progress quickly got into the game. The vast majority of new forks have sprung from Litecoin, inheriting scrypt instead of SHA256.
Strangely enough, users were not embarrassed by the fact that the 128 KB parameters were completely in the teeth and video cards. The optimized GPU miner appeared a few months later and gave an average of a tenfold increase in efficiency. “But not 100 times as in Bitcoin!” They said, “But not 1000 times!” The increase in the ratio of GPU / CPU-capacities (displaced from Bitcoin by new ASICs) was not so sharp, probably because what was compensated for the forks boom: a new scrypt-cryptocurrency appeared almost once a week, putting off new capacities.
And yet, the understanding that scrypt is far from an ideal PoW function appeared even earlier than the announcement of scrypt-ASIC. The dizziness from successes passed, the cult of Satoshi subsided a bit, and ideas for new PoW candidates began to appear as after the rain.
Read in the next series :
“Cross and multiply: X11 and Co. algorithms!”
“Atavisms against rudiments: SHA3 or scrypt-jane?”
“Paradoxes of history: Momentum and birthday paradox”
“Where is the peak of evolution: in theoretical computer science or practical? CuckooCycle and CryptoNight »
Source: https://habr.com/ru/post/263769/
All Articles