OpenCV and the illusion of circles on the water
I offer the readers of "Habrakhabr" an article about how school physics and OpenCV allow us to make the illusion of waves on the water. The main difficulty consists in choosing a beautiful equation and transferring the effect of light refraction at the interface between the three-dimensional world and the flat image.
The solution of the problem can be divided into two stages:
I suppose everyone from the school physics course remembers that the circles on the water are nothing but the propagation of oscillations over the surface of the water. A rigorous approach to solving a problem involves solving a differential wave equation in a two-dimensional space, but in our case, complete physical accuracy is not required — you can take a ready-made solution from a school textbook on physics or invent your own equation.

')
where c is the attenuation coefficient; L is the wavelength; x 0 , y 0 - coordinates of the wave center; t-time. The wavelength is better to change depending on the size of the image.
From the school course, remember that cosine takes the values [-1; 1], but the intensity of the color is [0; 255], therefore it is necessary to slightly modify our wave function. Finally, the brightness of each pixel on a layer with a wave is set as follows:
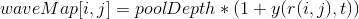
poolDepth is the thickness of the water layer, in this case, also the amplitude of the wave at the initial moment of time. Too much value will lead to significant distortion of the image and it will be ugly, too small - almost no effect on the picture. For the 100x100 picture, the value poolDepth = 20 came up, for the 1600x1600 picture it was possible to set the limit value poolDepth = 127.
Note that the size of the wavemap corresponds to the size of the original image. Taking into account the fact that the wave function is calculated at each point, we obtain a huge amount of computations already for a relatively small image (at each point we calculate one square root, one exponent and two cosines - a rare laptop will draw a 2MP picture in this scenario). In fact, at each point it is not necessary to calculate explicitly - the equation is a one-dimensional! At each time step we create a table of wave function values, and then linear interpolation.
Now we have a more or less decent implementation of the wave motion mapping algorithm, and we can proceed to its imposition on the original image.
The distortion of the image is under water due to the refraction of light at the interface. In fact, it is required to solve a school puzzle about the refraction of light on a wedge.
With a normal incidence of light on a flat horizontal interface, no distortion occurs (no change in the color of the picture as a result of interference is considered here - we believe that the puddle is not deep and we don’t pretend to 100% physical accuracy).

The figure shows what happens with the beam of light falling on an inclined surface; it is necessary to find how far the outgoing beam has shifted relative to the incoming one. The distance CD is the desired offset, defined as ( solution here ):
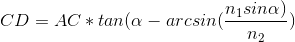
where n 1 = 1 and n 2 = 1.33 are the refractive indices of the first (air) and second (water) medium, respectively.
With reference to our waves and pixels, the equation can be written as:
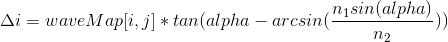
In this case, alpha is the angle of inclination of the tangent to the wave at point [i, j], which is calculated as:
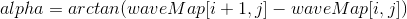
Of course, the derivative can also be calculated analytically, which will increase accuracy, but this will make the process of changing the wave equation time-consuming.
In this case, again we can either calculate the offset for each image point separately (void makeWaveMap (Mat &)), but it is better to lookup the table when the subroutine is first called and use it later (void makeWaveMapLUT (Mat &)).
The full text of the program, as well as test images here .
The average processing time (creating a wave map and overlaying the original image) of a single frame for a 1600x1600 image was 0.137sec and 0.415sec with and without lookup tables, respectively (100x100 pixels on the video).
The solution of the problem can be divided into two stages:
- Create a map of the propagation of circles / waves in the water;
- Combine the resulting card with the specified image.
Wave map
I suppose everyone from the school physics course remembers that the circles on the water are nothing but the propagation of oscillations over the surface of the water. A rigorous approach to solving a problem involves solving a differential wave equation in a two-dimensional space, but in our case, complete physical accuracy is not required — you can take a ready-made solution from a school textbook on physics or invent your own equation.

')
where c is the attenuation coefficient; L is the wavelength; x 0 , y 0 - coordinates of the wave center; t-time. The wavelength is better to change depending on the size of the image.
From the school course, remember that cosine takes the values [-1; 1], but the intensity of the color is [0; 255], therefore it is necessary to slightly modify our wave function. Finally, the brightness of each pixel on a layer with a wave is set as follows:
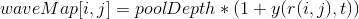
poolDepth is the thickness of the water layer, in this case, also the amplitude of the wave at the initial moment of time. Too much value will lead to significant distortion of the image and it will be ugly, too small - almost no effect on the picture. For the 100x100 picture, the value poolDepth = 20 came up, for the 1600x1600 picture it was possible to set the limit value poolDepth = 127.
Wavemap without lookup table
void makeWaveMap(Mat& image) { float simulPeriod = 10.0; // Period of simulation static float time = 0.0; const float dt = 0.05; // Time step float poolDepth = 20.0; int maxImageSize = image.cols > image.rows ? image.cols : image.rows; for (int i = 0; i < image.rows; i++) { for (int j = 0; j < image.cols; j++) { float radius = sqrt((i - image.rows/2)*(i - image.rows/2) + \ (j - image.cols/2)*(j - image.cols/2)); float z = (1.0 + waveFunction(radius, time, maxImageSize))*poolDepth; image.at<uchar>(i, j) = saturate_cast<uchar>(z); } } time+= dt; time*= (time < simulPeriod); } Note that the size of the wavemap corresponds to the size of the original image. Taking into account the fact that the wave function is calculated at each point, we obtain a huge amount of computations already for a relatively small image (at each point we calculate one square root, one exponent and two cosines - a rare laptop will draw a 2MP picture in this scenario). In fact, at each point it is not necessary to calculate explicitly - the equation is a one-dimensional! At each time step we create a table of wave function values, and then linear interpolation.
Wave card with lookup table
void makeWaveMapLUT(Mat& image) { float simulPeriod = 10.0; // Period of simulation static float time = 0.0; const float dt = 0.05; // Time step float poolDepth = 20.0; int nLUT = image.cols > image.rows ? image.cols : image.rows; int maxImageSize = nLUT; float waveFuncLUT[nLUT]; for (int i = 0; i < nLUT; i++) { float radius = saturate_cast<float>(i); waveFuncLUT[i] = waveFunction(radius, time, maxImageSize); } for (int i = 0; i < image.rows; i++) { for (int j = 0; j < image.cols; j++) { float radius = sqrt((i - image.rows/2)*(i - image.rows/2) + \ (j - image.cols/2)*(j - image.cols/2)); int iRad = cvRound(radius); float dR = radius - saturate_cast<float>(iRad); float wF = waveFuncLUT[iRad] + (waveFuncLUT[iRad+1] - waveFuncLUT[iRad])*dR; float z = (1.0 + wF)*poolDepth; image.at<uchar>(i, j) = saturate_cast<uchar>(z); } } time+= dt; time*= (time < simulPeriod); } Now we have a more or less decent implementation of the wave motion mapping algorithm, and we can proceed to its imposition on the original image.
Overlaying the wavemap onto the original image
The distortion of the image is under water due to the refraction of light at the interface. In fact, it is required to solve a school puzzle about the refraction of light on a wedge.
With a normal incidence of light on a flat horizontal interface, no distortion occurs (no change in the color of the picture as a result of interference is considered here - we believe that the puddle is not deep and we don’t pretend to 100% physical accuracy).

The figure shows what happens with the beam of light falling on an inclined surface; it is necessary to find how far the outgoing beam has shifted relative to the incoming one. The distance CD is the desired offset, defined as ( solution here ):
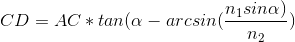
where n 1 = 1 and n 2 = 1.33 are the refractive indices of the first (air) and second (water) medium, respectively.
With reference to our waves and pixels, the equation can be written as:
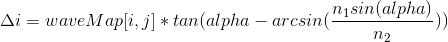
In this case, alpha is the angle of inclination of the tangent to the wave at point [i, j], which is calculated as:
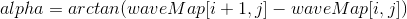
Of course, the derivative can also be calculated analytically, which will increase accuracy, but this will make the process of changing the wave equation time-consuming.
In this case, again we can either calculate the offset for each image point separately (void makeWaveMap (Mat &)), but it is better to lookup the table when the subroutine is first called and use it later (void makeWaveMapLUT (Mat &)).
Overlay without lookup tables
void blendWaveAndImage(Mat& sourceImage, Mat& targetImage, Mat& waveMap) { static float rFactor = 1.33; // refraction factor of water for (int i = 1; i < sourceImage.rows-1; i++) { for (int j = 1; j < sourceImage.cols-1; j++) { float alpha, beta; float xDiff = waveMap.at<uchar>(i+1, j) - waveMap.at<uchar>(i, j); float yDiff = waveMap.at<uchar>(i, j+1) - waveMap.at<uchar>(i, j); alpha = atan(xDiff); beta = asin(sin(alpha)/rFactor); int xDisplace = cvRound(tan(alpha - beta)*waveMap.at<uchar>(i, j)); alpha = atan(yDiff); beta = asin(sin(alpha)/rFactor); int yDisplace = cvRound(tan(alpha - beta)*waveMap.at<uchar>(i, j)); Vec3b Intensity = sourceImage.at<Vec3b>(i,j); /* Check whether displacement fits the image size */ int dispNi = i + xDisplace; int dispNj = j + yDisplace; dispNi = (dispNi > sourceImage.rows || dispNi < 0 ? i : dispNi); dispNj = (dispNj > sourceImage.cols || dispNj < 0 ? j : dispNj); Intensity = sourceImage.at<Vec3b>(dispNi, dispNj); targetImage.at<Vec3b>(i,j) = Intensity; } } } Overlay with lookup table
void blendWaveAndImageLUT(Mat& sourceImage, Mat& targetImage, Mat& waveMap) { static float rFactor = 1.33; // refraction factor of water static float dispLUT[512]; //Lookup table for displacement static int nDispPoint = 512; for (int i = 0; i < nDispPoint; i++) { float diff = saturate_cast<float>(i - 255); float alpha = atan(diff); float beta = asin(sin(alpha)/rFactor); dispLUT[i] = tan(alpha - beta); } nDispPoint = 0; for (int i = 1; i < sourceImage.rows-1; i++) { for (int j = 1; j < sourceImage.cols-1; j++) { int xDiff = waveMap.at<uchar>(i+1, j) - waveMap.at<uchar>(i, j); int yDiff = waveMap.at<uchar>(i, j+1) - waveMap.at<uchar>(i, j); int xDisplace = cvRound(dispLUT[xDiff+255]*waveMap.at<uchar>(i, j)); int yDisplace = cvRound(dispLUT[yDiff+255]*waveMap.at<uchar>(i, j)); Vec3b Intensity = sourceImage.at<Vec3b>(i,j); /* Check whether displacement fits the image size */ int dispNi = i + xDisplace; int dispNj = j + yDisplace; dispNi = (dispNi > sourceImage.rows || dispNi < 0 ? i : dispNi); dispNj = (dispNj > sourceImage.cols || dispNj < 0 ? j : dispNj); Intensity = sourceImage.at<Vec3b>(dispNi, dispNj); targetImage.at<Vec3b>(i,j) = Intensity; } } } The full text of the program, as well as test images here .
The results of the program in pictures and numbers
The average processing time (creating a wave map and overlaying the original image) of a single frame for a 1600x1600 image was 0.137sec and 0.415sec with and without lookup tables, respectively (100x100 pixels on the video).
Source: https://habr.com/ru/post/261477/
All Articles