Persistent queue
Inspired by the recent publication “Persistent Cartesian Tree by Implicit Key” , I decided to write about the implementation of the persistent queue. Those who thought now that once a normal queue is a trivial structure, then its persistent variant should be very simple, made a mistake, the resulting implementation is at least no simpler than for the above tree.
We will naturally implement the so-called full persistence - this means that intermediate versions are available not only in read-only mode and we can add and extract elements from them at any time. In addition, we, of course, would like to have the same asymptotics of the operating time and additional memory as for the non-persistent variant, namely O (n), where n is the total number of operations performed with our queue. By the way, if you weaken the requirements to O (n log n), then the queue is trivially emulated using a persistent Cartesian tree using an implicit key.
Let's take the following simple interface for working with our data structure: the resulting queue versions will be numbered with non-negative integers, initially there is only an empty queue number 0. Let us have N queue versions (including the initial one), then they are numbered from 0 to N-1 and we can execute the following four queries:
')
As you know , a persistent stack is a very simple data structure and its asymptotics is what we need. In addition, we know that the queue can be simulated using two stacks. An obvious idea arises: let's make these two stacks persistent and the problem is solved! Unfortunately, such a simple approach will not work. The thing is that with this imitation, not every operation has the asymptotics O (1): if the pop from which the stack from which we get the elements is empty, then we shift all the elements from the other stack to it. In the case of a normal queue, each element is shifted only once, so the total asymptotics remains O (n), but in the persistent case each element can belong to many queues and, accordingly, be shifted several times. Let, for example, q be the queue number for which this stack is empty, then after push (q, 1) and push (q, 2) for the received queues this stack will remain empty and with pop'e of them each element of the queue q will be shifted twice. To organize any sharing of the shifted elements is impossible due to the fact that the lowermost elements of the rearrangement received stacks will be different (1 and 2, respectively), and the persistent stack is arranged in such a way that each element stores a pointer to the element lying below it, therefore, in any case, we will be forced to have 2 copies of the penultimate element, which will point to the corresponding last, and hence 2 copies of the preceding last, to point to the desired last but one, and so on along the chains .
Nevertheless, there is an algorithm based on such an idea (imitation of a queue using two stacks), which guarantees that the stack that we get from pop'e will never be empty and will use 6 stacks to ensure this. My algorithm does not use this idea explicitly, although with common moments, of course, you can find it.
We will try to use the same structure as in the implementation of the persistent stack: we will store the added elements in the form of a tree (more precisely, a set of trees - forests), at each vertex there will be an added element and a pointer to the preceding one in the queue (more precisely, to the corresponding the previous element of the top of the tree). Speaking further element of the queue, I will often mean it is the corresponding top of the element.
A non-empty queue in such a case can be represented by a pair of pointers to the first and last element of the queue, and the vertex corresponding to the first element will necessarily be the ancestor of the vertex corresponding to the last (well, or coincide with it in the case of a queue of one element). An example of such a structure and displaying a queue in it:
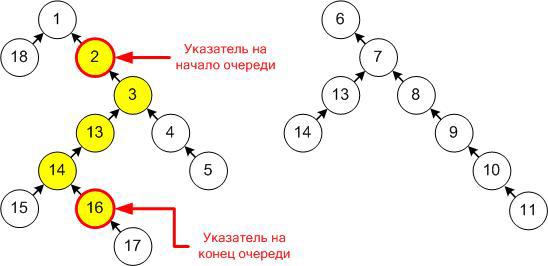
Note that the push operation simply creates a new vertex, setting its parent as the last element of the original queue (or it becomes a new root if added to an empty one), and the pop operation does not touch our forest at all, just moves the pointer to the first element. Thus, after creation, the vertex remains unchanged until the end of the work and it is possible not to worry that new operations may in some way spoil existing queues.
Our only problem with this approach is the implementation of the pop operation (the other three are trivial), it is not clear how to determine which vertex to move the pointer to the first element, because for the vertex we store only the pointer to the parent, but not to the sons (of which there may be several pieces, and even if all of them are stored, it is completely unclear which of them corresponds to the next element of our turn). Therefore, for each queue in which there are more than two elements, we will additionally store a pointer to an element of some simply connected list, such that the list element by our pointer contains a pointer to the second element of our queue, and the elements below it in the list, the third pointer, fourth and so on, respectively. Having such an index for the initial queue, when pops up, it will not be difficult for us to define a new queue head, and a pointer to such an element of the list for the resulting queue is just a pointer to the next element in this list.
However, for reasons similar to those for which the emulation of a queue with two stacks does not work, to ensure that for each queue below the list all its intermediate peaks lie, it will not work for us, therefore, let it be, it will contain only how many first of them, and we, when this list starts to become too small, we will build a new list, moving step by step (that is, increasing the list under construction by 1 element with each push or pop operation) from the end of the queue to the beginning, following the signs on parents of our tree tops but also trying to keep to the point where the old list is complete, we already had a new alert.
Speaking more formally, for each queue, in addition to pointers to the beginning and end, and a pointer to an element of an already prepared list, we will also keep a pointer to an element of the list under construction (if we do not build anything, it will be 0) and calculate its value for a new queue (obtained after applying to the original push'a or pop'a) according to the following simple algorithm:
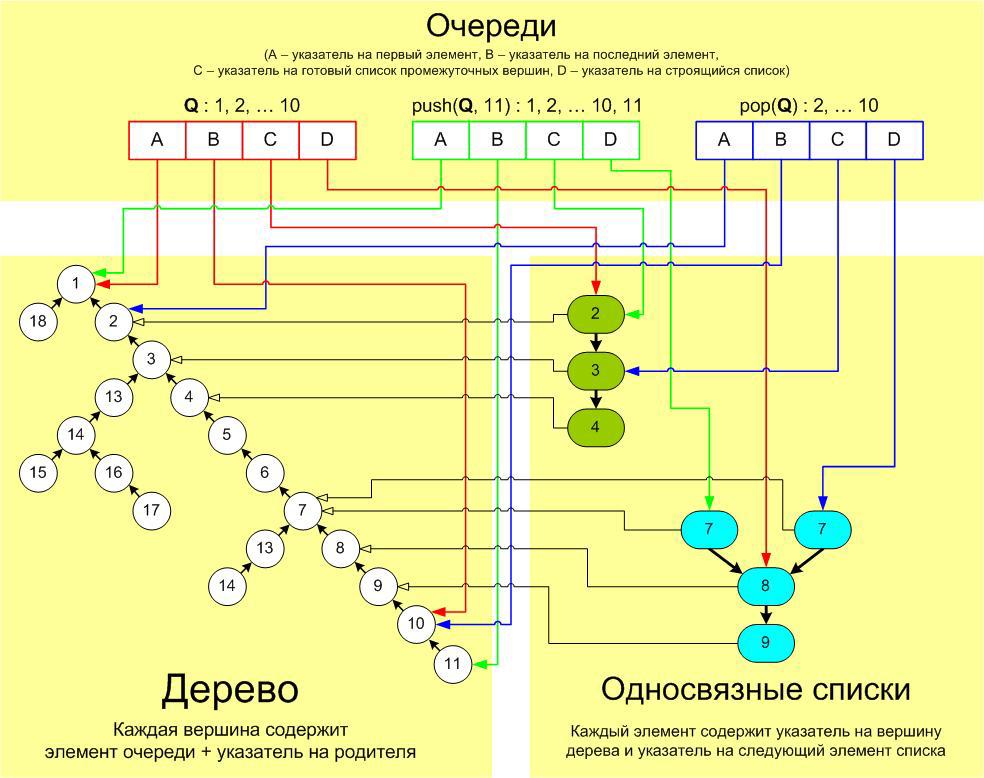
At the same time, neither the original element of the list, nor the pointer to it stored for the original queue, we will not change, and in general, we have all the data (tree nodes, list elements, data stored for the queues) will be immutable (that is, after creating will never change their meaning). An image of how it all works and what happens when push'e or pop'e can be seen in the diagram (it could not be made more understandable, no matter how hard I tried):
Accordingly, if during the completion of the list we reach the first intermediate element, then the construction for this queue is completed (while some other queues may continue to finish building this list, but since the old elements never change, it will not harm us in any way). In this case, we replace the pointer to the element of the old list with a pointer to the new element, and assign a pointer to the constructed list to zero.
From the description of the algorithm it is clear that during the execution of each request, we create no more than one new vertex of the tree and no more than one new element of the list and spend time on O (1) execution, that is, the asymptotics is the one we were trying to do, and it remains only to discuss the correct criterion.
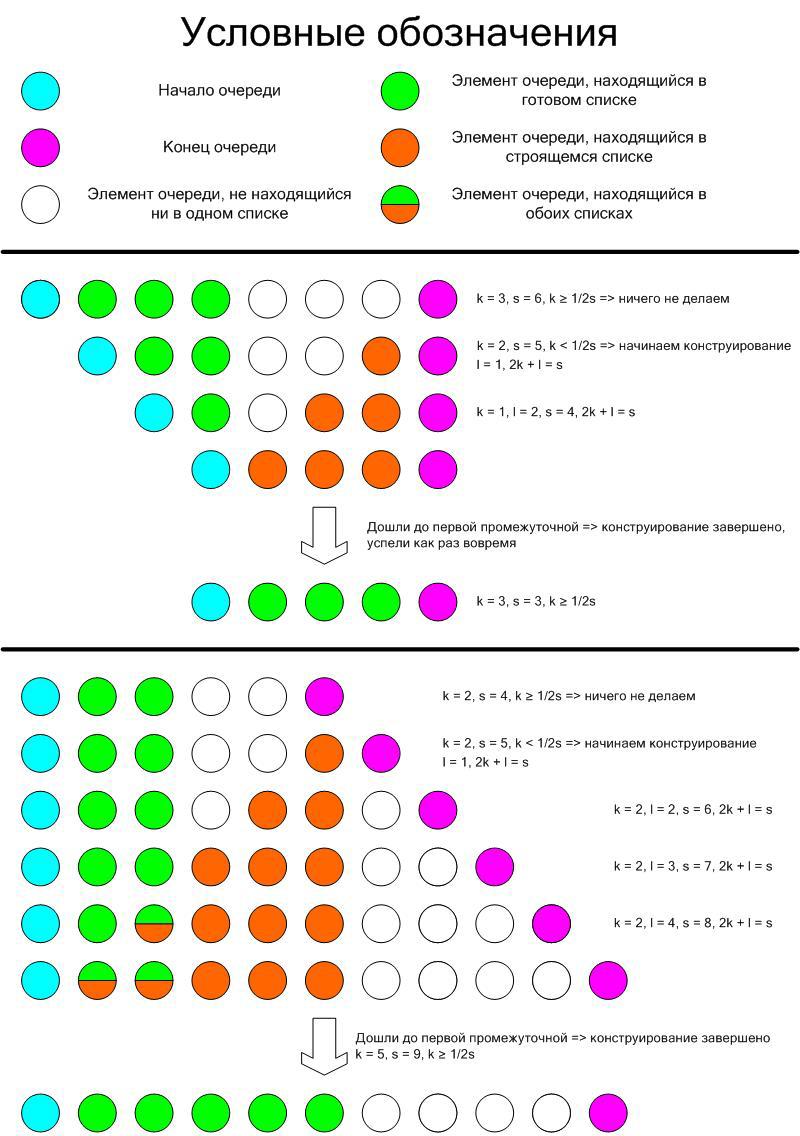
We will act as follows: as long as the size of our list is more or equal to 1/2 of the number of intermediate vertices (that is, vertices without the first and last), we do not do anything, as soon as it becomes smaller, we begin to construct a new one. Note that if there are no intermediate vertices, then we have the inequality 0 ≥ 0 and do nothing, that is, in a special case, it is not necessary to select it. Let us prove that with such an approach we will never find ourselves in a situation when the old list is over, and the new one is not yet ready.
To begin with, we prove the following invariant: if we construct a new list, then at each step 2k + l = s, where k is the number of elements in the old list, l is in the constructed (after the completion already completed at this step), s is the total number of intermediate items. We will prove by the method of mathematical induction. Consider the first step when we just started the design (l = 1). Note that for the new queue 2k - s <0 (our criterion), however, for the original 2k old - s old ≥ 0. Let's see how this could happen: if our operation is push, then k = k old and s = s old + 1, and if pop, then k = k old - 1 and s = s old - 1. As it is easy to see, in both cases 2k - s is less than 2k old - s old exactly by one and, since both differences are integers it means that the second of them is 0, and the first is -1, therefore, 2k + 1 = s, and our l is just one. The base of induction is proven. Let us prove the transition: let at some construction step 2k old + l old = s old . Then l = l old + 1 (added a list to 1 element), in the case of push'a: k = k old , s = s old + 1, in the case of pop'a: k = k old - 1, s = s old - 1. In both cases, the equality holds, and therefore the statement is proved.
Suppose now that we are doing a pop operation, and the source queue has the list we need is empty (with push, we don’t use this list). Then maybe one of two things:
It remains only to prove that when we complete the construction, the condition for the absence of construction is satisfied, that is, the length of the resulting list is no less than 1/2 of the total number of intermediate vertices, in other words, that at the time of completion 2l ≥ s or, equivalently, l ≥ s - l. But what is s - l? This is the number of intermediate vertices that are not contained in our list. It is easy to understand that it is equal to the number of push operations that occurred in the design process. However, with each such operation, the number of items in our list also increased by 1 (it is possible that in the previous step the item in the constructed list corresponds to the third item in the queue and we pop, then for the new queue the list item begins to correspond to the first intermediate item right away without finishing , but this is possible only at the last design step and only with the pop operation. Therefore, l ≥ the number of such push'ey (it is not difficult to understand that even strictly more), which we needed to prove.
For clarity, we will demonstrate what happens in two extreme cases: when we perform pop all the time and when we push all the time:
Finally, I will give an implementation of the above-described data structure in C ++ (the implementation uses C ++ 11 innovations). It is necessary to take this code as a prototype, I tried to write it as easy and shorter as possible, sacrificing everything else for this.
The TreeNode, Queue, and QueueIntermediateTreeNodeList types correspond to the top of the tree, the queue, and the element of the simply linked list from our algorithm. The Boolean variables in Queue are used to correctly free memory in the destructor of our class: the top of the tree and the list item remove the queue that created them (as noted above, with each request, no more than one vertex and no more than one list item are created). A tree vertex is created only during a push operation and a pointer to it is written to last, respectively, own_last indicates whether a new or old vertex is written to last. The element of the list created during construction is almost always recorded in constructing_intermediate_list, except when it was created and the construction at the same step ended, in which case it is transferred to known_intermediate_list, and constructing_intermediate_list becomes zero, and the second boolean variable own_known_intermediate_list is used for identification such a case.
The second possibly non-obvious point is the private member function manage_intermediate_lists, which looks like this:
This function implements the above described algorithm for working with a pointer to a list under construction (note that the first three parameters are transmitted via a non-constant link, and for the first two it is assumed that the variables by reference are initialized with the necessary values before the call). Before completing the list it is important to first check whether the old element has become the first intermediate one, because, as already noted, in the case of pop, this option is possible. Maybe someone noticed that we always check on our criterion for the beginning of the design:
First, as can be seen in the diagram , when performing several different operations with the same queue, for which construction is in progress (in the diagram, these are pop (Q) and push (Q, 11) operations), several absolutely identical elements are created list (they indicate the same next element and the same top of the tree - in the diagram there are two blue circles with the number 7). We could try to “glue” such elements into one, using, for example, a structure that would tell us when it was completed, and if someone had already done it before us (a banal vector or a doubly linked list can be used as such a structure). Obviously, such optimization will work well (save a lot of memory) in the case of heavily branched trees.
Secondly, we have another duplication: when the elements of the finished and under construction list point to the same top of the tree (we are talking about the green-orange elements in this picture). Of course, this duplication cannot be completely avoided, because the lists may well have the same beginning and continuations differing from each other, however, we could, when the first of the lists under construction reach the end of the finished (and not the beginning of the queue), simply “glue” it to this end, thereby saving a little memory. For the remaining lists (corresponding to this ready, of course), you still have to duplicate. Thus, this optimization will best manifest itself when we have many long straight branches on the trees.
Finally, thirdly, you can try to play with constants. For example, it is possible to complete construction in a step not on 1 element, but on 2, then it is enough to begin construction at k <1 / 3s. Perhaps it will be somehow useful.
That's all, thanks to everyone who read it.
Formulation of the problem
We will naturally implement the so-called full persistence - this means that intermediate versions are available not only in read-only mode and we can add and extract elements from them at any time. In addition, we, of course, would like to have the same asymptotics of the operating time and additional memory as for the non-persistent variant, namely O (n), where n is the total number of operations performed with our queue. By the way, if you weaken the requirements to O (n log n), then the queue is trivially emulated using a persistent Cartesian tree using an implicit key.
Let's take the following simple interface for working with our data structure: the resulting queue versions will be numbered with non-negative integers, initially there is only an empty queue number 0. Let us have N queue versions (including the initial one), then they are numbered from 0 to N-1 and we can execute the following four queries:
- empty (query_id) - checks if the queue with the specified number is empty;
- front (query_id) - returns the first element of the queue, the queue itself does not change at all and no new queues are created. The operation is valid if the queue is not empty;
- push (query_id, new_element) - creates a new queue number N, resulting in appending to the end of the original new item. The old version is still available under the number query_id;
- pop (query_id) - creates a new queue, numbered N, which is obtained by extracting from the original first element. The original queue is also all available under the old number. In the event that the original queue was empty, the new one will also be empty.
')
Imitation queue using stacks
For every problem there is a solution that is simple, fast, and wrong.
- The First Law of Online Judges
As you know , a persistent stack is a very simple data structure and its asymptotics is what we need. In addition, we know that the queue can be simulated using two stacks. An obvious idea arises: let's make these two stacks persistent and the problem is solved! Unfortunately, such a simple approach will not work. The thing is that with this imitation, not every operation has the asymptotics O (1): if the pop from which the stack from which we get the elements is empty, then we shift all the elements from the other stack to it. In the case of a normal queue, each element is shifted only once, so the total asymptotics remains O (n), but in the persistent case each element can belong to many queues and, accordingly, be shifted several times. Let, for example, q be the queue number for which this stack is empty, then after push (q, 1) and push (q, 2) for the received queues this stack will remain empty and with pop'e of them each element of the queue q will be shifted twice. To organize any sharing of the shifted elements is impossible due to the fact that the lowermost elements of the rearrangement received stacks will be different (1 and 2, respectively), and the persistent stack is arranged in such a way that each element stores a pointer to the element lying below it, therefore, in any case, we will be forced to have 2 copies of the penultimate element, which will point to the corresponding last, and hence 2 copies of the preceding last, to point to the desired last but one, and so on along the chains .
Nevertheless, there is an algorithm based on such an idea (imitation of a queue using two stacks), which guarantees that the stack that we get from pop'e will never be empty and will use 6 stacks to ensure this. My algorithm does not use this idea explicitly, although with common moments, of course, you can find it.
Algorithm Description
We will try to use the same structure as in the implementation of the persistent stack: we will store the added elements in the form of a tree (more precisely, a set of trees - forests), at each vertex there will be an added element and a pointer to the preceding one in the queue (more precisely, to the corresponding the previous element of the top of the tree). Speaking further element of the queue, I will often mean it is the corresponding top of the element.
A non-empty queue in such a case can be represented by a pair of pointers to the first and last element of the queue, and the vertex corresponding to the first element will necessarily be the ancestor of the vertex corresponding to the last (well, or coincide with it in the case of a queue of one element). An example of such a structure and displaying a queue in it:

Note that the push operation simply creates a new vertex, setting its parent as the last element of the original queue (or it becomes a new root if added to an empty one), and the pop operation does not touch our forest at all, just moves the pointer to the first element. Thus, after creation, the vertex remains unchanged until the end of the work and it is possible not to worry that new operations may in some way spoil existing queues.
Our only problem with this approach is the implementation of the pop operation (the other three are trivial), it is not clear how to determine which vertex to move the pointer to the first element, because for the vertex we store only the pointer to the parent, but not to the sons (of which there may be several pieces, and even if all of them are stored, it is completely unclear which of them corresponds to the next element of our turn). Therefore, for each queue in which there are more than two elements, we will additionally store a pointer to an element of some simply connected list, such that the list element by our pointer contains a pointer to the second element of our queue, and the elements below it in the list, the third pointer, fourth and so on, respectively. Having such an index for the initial queue, when pops up, it will not be difficult for us to define a new queue head, and a pointer to such an element of the list for the resulting queue is just a pointer to the next element in this list.
However, for reasons similar to those for which the emulation of a queue with two stacks does not work, to ensure that for each queue below the list all its intermediate peaks lie, it will not work for us, therefore, let it be, it will contain only how many first of them, and we, when this list starts to become too small, we will build a new list, moving step by step (that is, increasing the list under construction by 1 element with each push or pop operation) from the end of the queue to the beginning, following the signs on parents of our tree tops but also trying to keep to the point where the old list is complete, we already had a new alert.
Speaking more formally, for each queue, in addition to pointers to the beginning and end, and a pointer to an element of an already prepared list, we will also keep a pointer to an element of the list under construction (if we do not build anything, it will be 0) and calculate its value for a new queue (obtained after applying to the original push'a or pop'a) according to the following simple algorithm:
- if this pointer was equal to 0 for the initial queue, check if it’s time for us to start building a new list (the criterion for such a check will be described just below):
- if it is time, we create a list item with a zero pointer to the next one in the list (thus this created item will be the end of the constructed list), and we put the pointer to the top on the penultimate element of our turn (the parent of the last item),
- if the time is not yet, then the pointer is left zero.
- In the case of a non-zero initial pointer, we will complete our list up one element: create a new element pointing to the original one as the next one in the list and to the parent of the vertex corresponding to this initial element.
At the same time, neither the original element of the list, nor the pointer to it stored for the original queue, we will not change, and in general, we have all the data (tree nodes, list elements, data stored for the queues) will be immutable (that is, after creating will never change their meaning). An image of how it all works and what happens when push'e or pop'e can be seen in the diagram (it could not be made more understandable, no matter how hard I tried):

Accordingly, if during the completion of the list we reach the first intermediate element, then the construction for this queue is completed (while some other queues may continue to finish building this list, but since the old elements never change, it will not harm us in any way). In this case, we replace the pointer to the element of the old list with a pointer to the new element, and assign a pointer to the constructed list to zero.
From the description of the algorithm it is clear that during the execution of each request, we create no more than one new vertex of the tree and no more than one new element of the list and spend time on O (1) execution, that is, the asymptotics is the one we were trying to do, and it remains only to discuss the correct criterion.
The test criterion at the beginning of construction
We will act as follows: as long as the size of our list is more or equal to 1/2 of the number of intermediate vertices (that is, vertices without the first and last), we do not do anything, as soon as it becomes smaller, we begin to construct a new one. Note that if there are no intermediate vertices, then we have the inequality 0 ≥ 0 and do nothing, that is, in a special case, it is not necessary to select it. Let us prove that with such an approach we will never find ourselves in a situation when the old list is over, and the new one is not yet ready.
To begin with, we prove the following invariant: if we construct a new list, then at each step 2k + l = s, where k is the number of elements in the old list, l is in the constructed (after the completion already completed at this step), s is the total number of intermediate items. We will prove by the method of mathematical induction. Consider the first step when we just started the design (l = 1). Note that for the new queue 2k - s <0 (our criterion), however, for the original 2k old - s old ≥ 0. Let's see how this could happen: if our operation is push, then k = k old and s = s old + 1, and if pop, then k = k old - 1 and s = s old - 1. As it is easy to see, in both cases 2k - s is less than 2k old - s old exactly by one and, since both differences are integers it means that the second of them is 0, and the first is -1, therefore, 2k + 1 = s, and our l is just one. The base of induction is proven. Let us prove the transition: let at some construction step 2k old + l old = s old . Then l = l old + 1 (added a list to 1 element), in the case of push'a: k = k old , s = s old + 1, in the case of pop'a: k = k old - 1, s = s old - 1. In both cases, the equality holds, and therefore the statement is proved.
Suppose now that we are doing a pop operation, and the source queue has the list we need is empty (with push, we don’t use this list). Then maybe one of two things:
- either for the original queue we did not start constructing a new list, then this queue has 2k ≥ s,
k = 0 => s = 0, which means that this is a queue of size 0, 1 or 2 and knowledge of its last element is enough to make pop'a, - either started, then l ≠ 0, due to the invariant 2k + l = s, k = 0 => l = s ≠ 0 => the constructed list was non-empty and contained all intermediate elements, which means we had to replace at that step and get a non-empty list.
It remains only to prove that when we complete the construction, the condition for the absence of construction is satisfied, that is, the length of the resulting list is no less than 1/2 of the total number of intermediate vertices, in other words, that at the time of completion 2l ≥ s or, equivalently, l ≥ s - l. But what is s - l? This is the number of intermediate vertices that are not contained in our list. It is easy to understand that it is equal to the number of push operations that occurred in the design process. However, with each such operation, the number of items in our list also increased by 1 (it is possible that in the previous step the item in the constructed list corresponds to the third item in the queue and we pop, then for the new queue the list item begins to correspond to the first intermediate item right away without finishing , but this is possible only at the last design step and only with the pop operation. Therefore, l ≥ the number of such push'ey (it is not difficult to understand that even strictly more), which we needed to prove.
For clarity, we will demonstrate what happens in two extreme cases: when we perform pop all the time and when we push all the time:

C ++ implementation
Finally, I will give an implementation of the above-described data structure in C ++ (the implementation uses C ++ 11 innovations). It is necessary to take this code as a prototype, I tried to write it as easy and shorter as possible, sacrificing everything else for this.
persistent_queue.h
#ifndef PERSISTENT_QUEUE_H #define PERSISTENT_QUEUE_H #include <cstdlib> #include <vector> using Element_type = int; class Persistent_queue { public: Persistent_queue(); ~Persistent_queue(); Persistent_queue(const Persistent_queue&) = delete; Persistent_queue& operator =(const Persistent_queue&) = delete; using Queue_id = size_t; static const Queue_id start_queue_id = 0; Queue_id push(Queue_id queue_id, const Element_type& value); Queue_id pop(Queue_id queue_id); const Element_type& front(Queue_id queue_id); size_t size(Queue_id queue_id); bool empty(Queue_id queue_id); private: struct TreeNode; struct QueueIntermediateTreeNodeList; struct Queue { const TreeNode* const first; const TreeNode* const last; const size_t size; const QueueIntermediateTreeNodeList* const known_intermediate_list; const QueueIntermediateTreeNodeList* const constructing_intermediate_list; const bool own_last; const bool own_known_intermediate_list; Queue(const TreeNode* const first, const TreeNode* const last, const size_t size, const QueueIntermediateTreeNodeList* const known_intermediate_list, const QueueIntermediateTreeNodeList* const constructing_intermediate_list, const bool own_last, const bool own_known_intermediate_list); ~Queue() = default; Queue(Queue&& source) = default; // needed for vector reallocation Queue(const Queue&) = delete; Queue& operator =(const Queue&) = delete; }; std::vector<Queue> queues_; Queue_id register_new_queue(const TreeNode* const first, const TreeNode* const last, const size_t size, const QueueIntermediateTreeNodeList* const known_intermediate_list, const QueueIntermediateTreeNodeList* const constructing_intermediate_list, const bool own_last, const bool own_known_intermediate_list); void manage_intermediate_lists(const QueueIntermediateTreeNodeList*& known_intermediate_list, const QueueIntermediateTreeNodeList*& constructing_intermediate_list, bool& own_known_intermediate_list, const TreeNode* const first, const TreeNode* const last, const size_t size); }; #endif // PERSISTENT_QUEUE_H persistent_queue.cpp
#include "persistent_queue.h" #include <cassert> struct Persistent_queue::TreeNode { const TreeNode* const parent; const Element_type element; TreeNode(const TreeNode* const parent, const Element_type& value) : parent(parent), element(value) {} ~TreeNode() = default; TreeNode(const TreeNode&) = delete; TreeNode& operator =(const TreeNode&) = delete; }; struct Persistent_queue::QueueIntermediateTreeNodeList { const Persistent_queue::TreeNode* const front; const QueueIntermediateTreeNodeList* const next; const size_t size; QueueIntermediateTreeNodeList(const Persistent_queue::TreeNode* const front, const QueueIntermediateTreeNodeList* const tail_list) : front(front), next(tail_list), size{tail_list ? tail_list->size + 1 : 1} { assert(front); } ~QueueIntermediateTreeNodeList() = default; QueueIntermediateTreeNodeList(const QueueIntermediateTreeNodeList&) = delete; QueueIntermediateTreeNodeList& operator =(const QueueIntermediateTreeNodeList&) = delete; }; Persistent_queue::Queue::Queue( const Persistent_queue::TreeNode* const first, const Persistent_queue::TreeNode* const last, const size_t size, const Persistent_queue::QueueIntermediateTreeNodeList* const known_intermediate_list, const Persistent_queue::QueueIntermediateTreeNodeList* const constructing_intermediate_list, const bool own_last, const bool own_known_intermediate_list ) : first(first), last(last), size(size), known_intermediate_list(known_intermediate_list) , constructing_intermediate_list(constructing_intermediate_list) , own_last(own_last), own_known_intermediate_list(own_known_intermediate_list) { // Some asserts if (size == 0) { assert(first == nullptr); assert(last == nullptr); } else { assert(first); assert(last); if (size > 1) assert(last->parent); } if (size <= 2) { assert(known_intermediate_list == nullptr); assert(constructing_intermediate_list == nullptr); if (size == 1) assert(first == last); if (size == 2) assert(first == last->parent); } else { assert(known_intermediate_list); assert(first == known_intermediate_list->front->parent); } } size_t Persistent_queue::size(const Persistent_queue::Queue_id queue_id) { return queues_.at(queue_id).size; } bool Persistent_queue::empty(const Queue_id queue_id) { return size(queue_id) == 0; } const Element_type& Persistent_queue::front(const Persistent_queue::Queue_id queue_id) { assert(!empty(queue_id)); return queues_.at(queue_id).first->element; } Persistent_queue::Queue_id Persistent_queue::register_new_queue(const TreeNode* const first, const TreeNode* const last, const size_t size, const QueueIntermediateTreeNodeList* const known_intermediate_list, const QueueIntermediateTreeNodeList* const constructing_intermediate_list, const bool own_last, const bool own_known_intermediate_list) { queues_.emplace_back(first, last, size, known_intermediate_list, constructing_intermediate_list, own_last, own_known_intermediate_list); return queues_.size() - 1; } Persistent_queue::Persistent_queue() { register_new_queue(nullptr, nullptr, 0, nullptr, nullptr, false, false); } Persistent_queue::~Persistent_queue() { for (const auto& q : queues_) { if (q.own_last) delete q.last; if (q.own_known_intermediate_list) delete q.known_intermediate_list; delete q.constructing_intermediate_list; } } Persistent_queue::Queue_id Persistent_queue::push(const Persistent_queue::Queue_id queue_id, const Element_type& value) { const auto& queue_for_push = queues_.at(queue_id); const size_t size = queue_for_push.size + 1; const bool own_last = true; const TreeNode* first; const TreeNode* last; if (queue_for_push.size == 0) { first = last = new TreeNode(nullptr, value); } else { first = queue_for_push.first; last = new TreeNode(queue_for_push.last, value); } bool own_known_intermediate_list; const QueueIntermediateTreeNodeList* known_intermediate_list = queue_for_push.known_intermediate_list; const QueueIntermediateTreeNodeList* constructing_intermediate_list = queue_for_push.constructing_intermediate_list; manage_intermediate_lists(known_intermediate_list, constructing_intermediate_list, own_known_intermediate_list, first, last, size); return register_new_queue(first, last, size, known_intermediate_list, constructing_intermediate_list, own_last, own_known_intermediate_list); } Persistent_queue::Queue_id Persistent_queue::pop(const Persistent_queue::Queue_id queue_id) { const auto& queue_for_pop = queues_.at(queue_id); const bool own_last = false; const TreeNode* first; const TreeNode* last; size_t size; const QueueIntermediateTreeNodeList* known_intermediate_list; if (queue_for_pop.size <= 1) { first = last = nullptr; size = 0; known_intermediate_list = nullptr; } else { last = queue_for_pop.last; size = queue_for_pop.size - 1; if (queue_for_pop.size == 2) { first = queue_for_pop.last; known_intermediate_list = nullptr; } else { assert(queue_for_pop.known_intermediate_list != nullptr); first = queue_for_pop.known_intermediate_list->front; known_intermediate_list = queue_for_pop.known_intermediate_list->next; } } bool own_known_intermediate_list; const QueueIntermediateTreeNodeList* constructing_intermediate_list = queue_for_pop.constructing_intermediate_list; manage_intermediate_lists(known_intermediate_list, constructing_intermediate_list, own_known_intermediate_list, first, last, size); return register_new_queue(first, last, size, known_intermediate_list, constructing_intermediate_list, own_last, own_known_intermediate_list); } void Persistent_queue::manage_intermediate_lists( const Persistent_queue::QueueIntermediateTreeNodeList*& known_intermediate_list, const Persistent_queue::QueueIntermediateTreeNodeList*& constructing_intermediate_list, bool& own_known_intermediate_list, const Persistent_queue::TreeNode* const first, const Persistent_queue::TreeNode* const last, const size_t size) { own_known_intermediate_list = false; const size_t intermediate_nodes_count = (size > 2 ? size - 2 : 0); size_t known_intermediate_list_size = (known_intermediate_list ? known_intermediate_list->size : 0); if (2*known_intermediate_list_size < intermediate_nodes_count) { auto try_to_replace_known_to_constructing = [&](){ if (constructing_intermediate_list && constructing_intermediate_list->front->parent == first) { known_intermediate_list = constructing_intermediate_list; known_intermediate_list_size = constructing_intermediate_list->size; constructing_intermediate_list = nullptr; return true; } return false; }; if (!try_to_replace_known_to_constructing()) { const auto adding_node = (constructing_intermediate_list ? constructing_intermediate_list->front->parent : last->parent); constructing_intermediate_list = new QueueIntermediateTreeNodeList( adding_node, constructing_intermediate_list); if (try_to_replace_known_to_constructing()) own_known_intermediate_list = true; } } // Check invariants if (2*known_intermediate_list_size >= intermediate_nodes_count) assert(constructing_intermediate_list == nullptr); const size_t constructing_intermediate_list_size = (constructing_intermediate_list ? constructing_intermediate_list->size : 0); const auto invariant_sum = 2*known_intermediate_list_size + constructing_intermediate_list_size; assert(invariant_sum >= intermediate_nodes_count); if (constructing_intermediate_list) assert(invariant_sum == intermediate_nodes_count); } The TreeNode, Queue, and QueueIntermediateTreeNodeList types correspond to the top of the tree, the queue, and the element of the simply linked list from our algorithm. The Boolean variables in Queue are used to correctly free memory in the destructor of our class: the top of the tree and the list item remove the queue that created them (as noted above, with each request, no more than one vertex and no more than one list item are created). A tree vertex is created only during a push operation and a pointer to it is written to last, respectively, own_last indicates whether a new or old vertex is written to last. The element of the list created during construction is almost always recorded in constructing_intermediate_list, except when it was created and the construction at the same step ended, in which case it is transferred to known_intermediate_list, and constructing_intermediate_list becomes zero, and the second boolean variable own_known_intermediate_list is used for identification such a case.
The second possibly non-obvious point is the private member function manage_intermediate_lists, which looks like this:
void Persistent_queue::manage_intermediate_lists( const Persistent_queue::QueueIntermediateTreeNodeList*& known_intermediate_list, const Persistent_queue::QueueIntermediateTreeNodeList*& constructing_intermediate_list, bool& own_known_intermediate_list, const Persistent_queue::TreeNode* const first, const Persistent_queue::TreeNode* const last, const size_t size) { own_known_intermediate_list = false; const size_t intermediate_nodes_count = (size > 2 ? size - 2 : 0); size_t known_intermediate_list_size = (known_intermediate_list ? known_intermediate_list->size : 0); if (2*known_intermediate_list_size < intermediate_nodes_count) { auto try_to_replace_known_to_constructing = [&](){ if (constructing_intermediate_list && constructing_intermediate_list->front->parent == first) { known_intermediate_list = constructing_intermediate_list; known_intermediate_list_size = constructing_intermediate_list->size; constructing_intermediate_list = nullptr; return true; } return false; }; if (!try_to_replace_known_to_constructing()) { const auto adding_node = (constructing_intermediate_list ? constructing_intermediate_list->front->parent : last->parent); constructing_intermediate_list = new QueueIntermediateTreeNodeList( adding_node, constructing_intermediate_list); if (try_to_replace_known_to_constructing()) own_known_intermediate_list = true; } } // Check invariants } This function implements the above described algorithm for working with a pointer to a list under construction (note that the first three parameters are transmitted via a non-constant link, and for the first two it is assumed that the variables by reference are initialized with the necessary values before the call). Before completing the list it is important to first check whether the old element has become the first intermediate one, because, as already noted, in the case of pop, this option is possible. Maybe someone noticed that we always check on our criterion for the beginning of the design:
if (2*known_intermediate_list_size < intermediate_nodes_count) { not singling out the case when construction is already underway. The fact is that during the whole design process our criterion will remain true, this obviously follows from our design invariant: 2k + l = s, l> 0 => 2k <s.Possible optimizations
First, as can be seen in the diagram , when performing several different operations with the same queue, for which construction is in progress (in the diagram, these are pop (Q) and push (Q, 11) operations), several absolutely identical elements are created list (they indicate the same next element and the same top of the tree - in the diagram there are two blue circles with the number 7). We could try to “glue” such elements into one, using, for example, a structure that would tell us when it was completed, and if someone had already done it before us (a banal vector or a doubly linked list can be used as such a structure). Obviously, such optimization will work well (save a lot of memory) in the case of heavily branched trees.
Secondly, we have another duplication: when the elements of the finished and under construction list point to the same top of the tree (we are talking about the green-orange elements in this picture). Of course, this duplication cannot be completely avoided, because the lists may well have the same beginning and continuations differing from each other, however, we could, when the first of the lists under construction reach the end of the finished (and not the beginning of the queue), simply “glue” it to this end, thereby saving a little memory. For the remaining lists (corresponding to this ready, of course), you still have to duplicate. Thus, this optimization will best manifest itself when we have many long straight branches on the trees.
Finally, thirdly, you can try to play with constants. For example, it is possible to complete construction in a step not on 1 element, but on 2, then it is enough to begin construction at k <1 / 3s. Perhaps it will be somehow useful.
That's all, thanks to everyone who read it.
Source: https://habr.com/ru/post/241231/
All Articles