Introduction

Having read recently an article about the list on Haskell, I decided to also talk a little about the implementation of the basic structures on the FNP (F #). The article does not carry practical value, since there are plenty of ready-made implementations on the Internet. The purpose of the article is to talk about how you can implement an immutable queue on F # and how it works.

First, a little bit of terminology.

F # is a programming language from the .NET family, which, in addition to the object-oriented and imperative approaches, implements a functional approach to programming.

Immutable objects are those objects that, once created, cannot be changed in the future. For example, in C # there is such a data type as string, instances of which are immutable. By adding a character to a string, you get a new string and have the old one unchanged. Read more here .

Singly linked list

To implement the queue, we need a single-linked list. Recall that a single-linked list is such a data structure, each element of which contains a stored value and a link to the previous element.

The same on F #:

type public 'a List = //  List  generic- 'a,     | Empty //  | Node of 'a * 'a List //:  -   ("") 

This record means that the list can either be empty, or be a pair of “head” - “tail”, where the “tail” is also a list.

Consider the basic operations on the list and evaluate their complexity.

Add item to list

To add an element and at the same time leave the old list unchanged, you need to create a new list, where head is the added element, tail is the old list. F # is written in one line:

 member this.Cons x = Node(x, this) 

After this, we already have two lists: the original and the new. In this case, both lists occupy the memory as much as one final list (see the figure below).



In Figure 1, the list is before the item is added, List2 is the list after the item is added. In this case, List1 is also the “tail” of List2.

Obviously, the complexity of adding an element does not depend on the length of the list and is equal to O (1).

')

Extract item from list

Removing an item is as easy as adding. The last added element is simply taken from the “head”; for a list without this element, take the "tail".

 member this.Head = match this with | Empty -> failwith "Empty stack" | Node(head, tail) -> head member this.Tail = match this with | Empty -> failwith "Empty stack" | Node(head, tail) -> tail 

Obviously, the complexity of these operations is O (1).

List reversal

Another useful list operation is a reversal, i.e. change the order of the elements. For a reversal, it is necessary to sequentially extract elements from the original list and place them in a new one. New and old lists will not have shared data. The complexity will always be O (N). Code and illustration below:

 let rec reverse destList sourceList = match sourceList with | Empty -> destList | Node(sourceHead, sourceTail) -> reverse (Node(sourceHead, destList)) sourceTail 

In Figure 1, the list before the reversal, List2 after.

Turn

A concatenated list with the operations of adding and extracting elements is ideal for implementing a stack. However, if you take a couple of such lists, you can implement a queue.

A queue is a data structure with the principle of access to the elements “first arrived, first out” (FIFO).

To implement the queue, you will need a rear (rear) list to which new elements are added, and a frontal (front) list from which elements are extracted.

 type 'a Queue (front:'a List, rear: 'a List) = //   Queue    static member Empty = Queue(List.Empty, List.Empty) //   -    

Add item to queue

Adding an element to the queue - this is adding an element to the rear list, or rather, creating a new queue, where the front list is the same, and the rear list is obtained by adding a new element:

  member this.Snoc value = Queue(front, rear.Cons value) 

Obviously, the estimate of the complexity of adding an element to the queue coincides with the estimate of the complexity of adding an element to the simply-connected list — O (1).

Retrieving an item from a queue

Before removing an element from the front list, check if it is empty. If it is empty, we take the rear and expand it - now it is frontal, and the rear list is an empty list. In the worst case, the complexity of extraction is equal to the complexity of turning the O (N) list.

  let frontToBack = match front, rear with |Empty, rear -> (rear.Reverse, Empty) |x -> (x) member this.Head = match frontToBack with | Empty, _ -> failwith "Empty or not reversed" | List.Node(a, __), _ -> a member this.Tail = match frontToBack with |Empty, _ -> failwith "Empty" |List.Node(a, tail), r -> Queue(tail, r) 

Below is an illustration of "life" queues, which shows the sequential execution of the operations of addition and extraction.



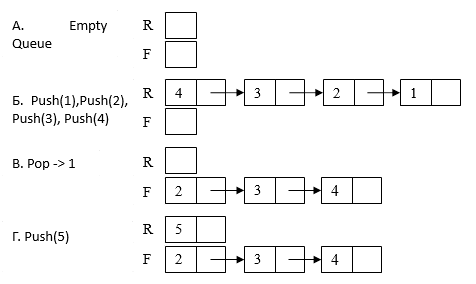
The figure shows four queues schematically: A is an empty queue, B is a queue after successive addition of numbers 1, 2, 3 and 4, C is a queue after extracting one element (number 1), G is a queue after adding number 5.

Conclusion

The single-linked list discussed at the beginning of the article can be used not only as a stack, but also as a collection with random access. This will require inserts and deletes. Their complexity depends on the place of insertion / deletion and in the worst case is O (N). I leave the implementation to the reader.

Both the list and the queue for some operations have not the best complexity - O (N). The situation can be improved up to O (1) if the implementation correctly applies lazy calculations. How this is done, I will tell in the next article, if the dear reader shows interest in the topic.

Used Books

Chris Okasaki’s “Purely Functional Data Structures” book was used as the main source of information.