Arrays, Collections: Algorithmic minimum

Arrays and Lists

Recently, during a job interview with a large company for the position of Java developer, I was asked to implement a standard sorting algorithm. Since I never implemented samopisnye sorting algorithms, but used always ready-made solutions, I had difficulty with the implementation. After the interview, I decided to sort out the question and prepare a list of the basic sorting and search algorithms that are used in the standard java package - the Java Collections Framework (JCF). For this, I studied the source code JDK 7.80.



In the most generalized form, the result of the study is presented in the figure. Details - in the main text.





')

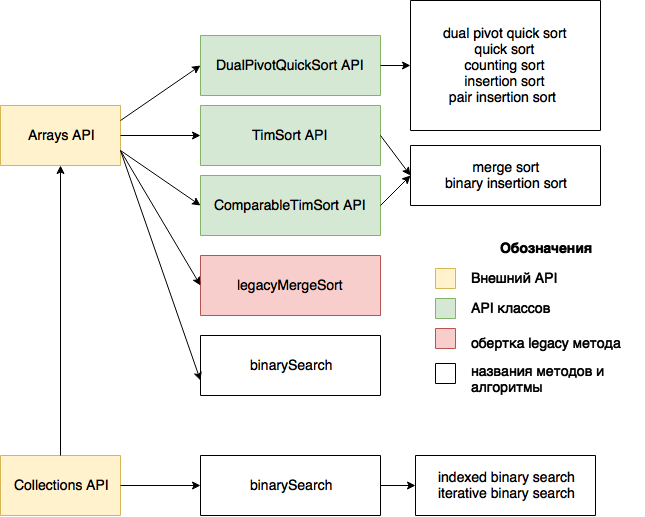
Figure 1. Arrays, Collections methods and algorithms implemented by them





The first thing that struck me in the algorithms implemented in Arrays and Collections is that they can literally be counted on the fingers - by and large, these are two sorting algorithms and one search algorithm.



The second is that sorting lists “under the hood” uses array sorting.



The third is that one of the sorting algorithms is ported with python.



The algorithm of quick sorting with two supporting elements was developed by our compatriot Vladimir Yaroslavsky and implemented with the assistance of John Bentley and Joshua Bloch.



The merge sorting algorithm, which is basic for sorting arrays of reference types, is literally named after the name of its creator Tim Peters - TimSort. This algorithm was adapted by Joshua Bloch from the list sorting algorithm implemented by Tim Peters in python.



Summarizing the results, it is worth noting that:

1. You can conditionally distinguish three layers of methods:
   
   
   • API methods
   • Methods of basic (basic) algorithms
   • Methods (blocks) of additional algorithms
2. There are three main algorithms. Two sorting algorithms: quick sort, merge sort. One search algorithm: binary search.
3. For optimization, the “basic” algorithms are replaced with the more appropriate “additional” algorithms at the moment (the full list of algorithms and switching conditions is given at the end)
4. To determine which of the "additional" algorithms will be used, can be used:
   
   
   • method signatures (argument types, boolean variables)
   • VM flags
   • array / list length thresholds stored in private variable classes

The util package for working with arrays and collections is intended for the Arrays and Collections classes, respectively. As a basic service, they provide methods for sorting and searching. For compatibility, the API Collections and the Arrays API are unified. The user is provided with static overloaded sort and binarySearch methods. The difference is that the Arrays API methods accept arrays of primitive and reference types, while the sort and binarySearch Collections API methods accept only lists.



So, in order to find out which main and additional algorithms are used in the util package, you need to parse the implementation of 4 methods from the API Collections and the Arrays API.



Table 1. API Arrays vs API Collections

Method	Arrays API	Collections API
Sort method	Arrays.sort	Collections.sort
Search method	Arrays.binarySearch	Collections.binarySearch

Arrays.sort

Arrays of primitive types

The basic sorting algorithm for arrays of primitive types in Arrays is quick sorting . To implement this sorting, the final class DualPivotQuickSort is allocated, which provides public sort methods for sorting arrays of all primitive data types. The Arrays API methods call these methods and send a reference to the array in them. If you want to sort a specific range of an array, then the indices of the beginning and end of the range are also transmitted.



The time complexity of the quick sort algorithm is O (n log n) at best and in the average case. In some cases (for example, on small arrays), the fast sorting algorithm has not the best performance, it degrades to quadratic complexity. Therefore, it makes sense to use other algorithms instead, which generally lose, but in specific cases can give a win. The additional algorithms were selected with sorting by inserts, “normal” quick sorting (with one reference point), sorting by counting .



Oracle empirically calculated the optimal dimensions of the arrays to enable each additional sorting algorithm. These values ​​are written in the private fields of the DualPivotQuickSort class. For clarity, I summarized them in table 2.



Table 2. Additional algorithms in DualPivotQuickSort.sort

Data types	Array size, n	Preferred algorithm	Time complexity at best
int, long, short, char, float, double	n <47	insertion sort pair insertion sort	O (n)
int, long, short, char, float, double	n <286	quick sort	O (n log n)
byte	29 <n	counting sort	O (n + k)
short, char	3200 <n	counting sort	O (n + k)

In the body of the DualPivotQuickSort.sort methods, checks are made for the length of the array, and depending on the result, either the main or the additional algorithm is applied.

Arrays of primitive types. The choice of the algorithm and the boolean parameter leftmost

The leftmost parameter is passed to the sort method, if necessary, and indicates whether the specified part is leftmost in the range. If yes, then the “normal” insert sorting algorithm is applied. If not, pairing sorting is applied.



Another explanation about the choice of additional algorithms can be read

here

Reference arrays

For arrays of reference types, the merge sorting algorithm is used as the main one; it is implemented in three variations. Two actual implementations are in special classes: TimSort, ComparableTimSort. TimSort is designed to sort objects using comparators. ComparableTimSort is a version of TimSort designed to sort objects that support Comparable. Details of the implementation of sorting TimSort, see the post on Habré .



The TimSort class contains a single threshold value, when compared with which a decision is made to switch to an additional algorithm. This value is called MIN_MERGE and stores the minimum length of the array at which merge sorting will be performed. If the array length is less than MIN_MERGE, i.e. 32, then the binary sorting by inserts will be involved. As stated in the documentation, this is a mini-TimSort, i.e. without the use of mergers.



Table 3. Additional algorithms in TimSort.sort and ComparableTimSort.sort

Data type	Array size, n	Preferred algorithm	Time complexity at best
T []	n <32	binary insertion sort	O (n)

The third implementation of merge sort is legacy and is left for backward compatibility with JDK 1.6 and earlier. Legacy sorting is wrapped in the legacyMergeSort method and directly implemented in the Arrays.mergeSort method. In order to use it, you must set the -Djava.util.Arrays.useLegacyMergeSort = true flag before starting the virtual machine. To store the value of this variable, Arrays has an internal static class LegacyMergeSort (see Listing. 1).



Listing 1. Static inner class LegacyMergeSort in Arrays

static final class LegacyMergeSort { private static final boolean userRequested = java.security.AccessController.doPrivileged( new sun.security.action.GetBooleanAction( "java.util.Arrays.useLegacyMergeSort")).booleanValue(); } 

When calling Arrays.sort with an array of a reference type, it checks whether the flag is set to use legacy sorting. Then there is a call to either the legacy sort, or one of the base ones (see Listing 2).



Listing 2. Implementing the Arrays.sort method for an array of reference type with a comparator

 public static <T> void sort(T[] a, Comparator<? super T> c) { if (LegacyMergeSort.userRequested) legacyMergeSort(a, c); else TimSort.sort(a, c); } 

Arrays.binarySearch

For arrays of both primitive and reference types, a binary search is provided. The array must be sorted before searching. The complexity of the binary search algorithm on average and in the worst case is O (log n). Additional algorithms are not provided.

Collections.sort

In Collections sorting is provided only for lists. Interestingly, the list is first converted into an array, followed by merge sorting for arrays of reference types. Sorting is done by calling the Arrays.sort method.

Collections.binarySearch

As in the case of sorting, in Collections binary search is implemented only for lists. The variable BINARYSEARCH_THRESHOLD sets a limit on the size of the list to 5000 items. So if you need to conduct a search on a more impressive sample, you will have to think about how to do it better.



Lists support either random access or sequential . If the list supports random access, it will be processed by an indexed binary search algorithm. If the list supports sequential access, then it will be processed by an iterative binary search algorithm. As you can see, in both cases, a binary search will be applied.



In total, the List interface in JDK 7.8 is implemented in 10 classes, 2 of which are Abstract Abstract and Abstract Sequential List. Sequential access is implemented only by LinkedList and all descendants of AbstractSequentialList. Therefore, they will be processed by the iteratorBinarySearch algorithm. The remaining lists, such as ArrayList, CopyOnWriteArrayList, will be processed by the indexedBinarySearch algorithm.



UPD. As it became clear from a personal discussion with Zamyslov , it is necessary to clarify how BINARYSEARCH_THRESHOLD participates in determining the type of sorting algorithm. This threshold value only affects sequential access lists.



A random access list will always be processed by Collections.indexedBinarySearch. A list that supports sequential access will be processed by Collections.iteratorBinarySearch only if it exceeds the BINARYSEARCH_THRESHOLD value (see listing 3), otherwise it will also be processed by Collections.indexedBinarySearch.



Listing 3. The effect of list types and the BINARYSEARCH_THRESHOLD constant on defining list processing algorithms

 int binarySearch(List<? extends Comparable<? super T>> list, T key) { if (list instanceof RandomAccess || list.size()<BINARYSEARCH_THRESHOLD) return Collections.indexedBinarySearch(list, key); else return Collections.iteratorBinarySearch(list, key); } 

Summarize the studied

Now that the main methods and conditions for the transition to additional methods are considered, the obtained data can be generalized. For maximum clarity, let's detail Figure 1, highlighting the main methods on it and add the conditions for the transition to additional methods.







Figure 2. Basic and advanced algorithms Arrays, Collections



The explanations for the numbers on the arrows in Figure 2 are contained in the Summary Table. Numbers indicate transition conditions. Gray highlights the main algorithms. They are applied by default. In the Pivot Table, the lines describing the basic algorithms are highlighted in dark gray.







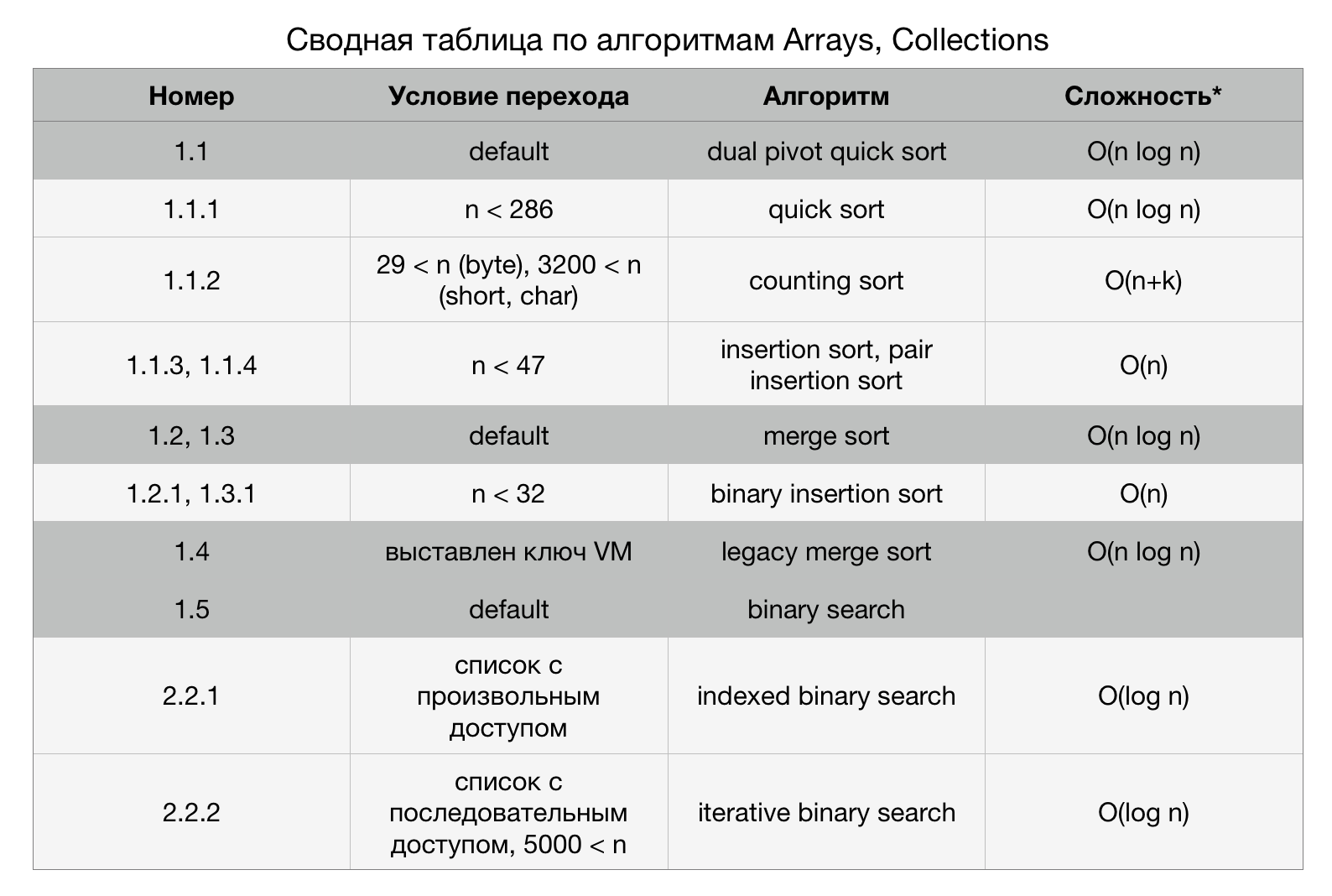
* Difficulties for the main algorithms are given “in the average case”, and the complexities of the additional algorithms are given “at best”.

Conclusion

The purpose of the note was to compile a complete list of algorithms used to search and sort arrays and lists in the java.util package. So, in order to fully understand what is happening “under the hood” when using the Arrays API and API Collections, it is enough to own the following algorithms:

1. quick sort with two control points
2. quick sort with one control point
3. counting sort
4. "Simple" sorting inserts
5. binary sorting inserts
6. pair sorting inserts
7. merge sorting (Tim Peters version)
8. binary search
9. indexed binary search
10. iterative binary search

Analysis of algorithms and their properties can be found on the links:

1. About sorting lists
2. Algorithms when processing arrays in Arrays
3. Know the complexity of the algorithms
4. Timsort sorting algorithm
5. Yaroslavskyy article on the quick sort algorithm Thanks for the link Maccimo
6. Algorithms of sorting in the form of step-by-step animation
7. Sequential and random access