Reed-Solomon codes. Part 2 - Galois Field Arithmetic
Hello, friends! Last time, you and I started talking about how Reed-Solomon codes help ensure the required level of data storage reliability. Today we’ll dwell on the arithmetic of the Galois fields, which is used in the calculations.

First, a brief excursion into the last part . We found out that in order to be able to recover lost data, you must first generate “redundant data” in a certain way. Moreover, from a mathematical point of view, this task (coding) is reduced to constructing a certain generating matrix and performing the operation of multiplying this matrix by the vector of the original data. The recovery (decoding) procedure, in turn, consists in inverting the generating matrix and multiplying it by the vector of the preserved data. Schematically it can be represented as follows.
Coding procedure:
')
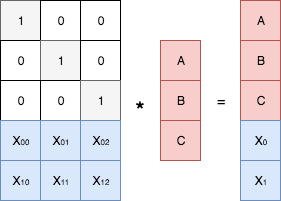
Decoding procedure:
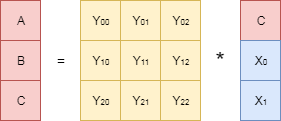
We have already noted some of the difficulties encountered in the implementation of encoding / decoding procedures on specific hardware platforms. For example, numbers in computer memory are usually represented by a fixed number of bytes. As a result, by multiplying the elements of the generating matrix, one can get an overflow of discharges. Or, when the generating matrix is addressed as its elements, rational numbers may arise that are problematic to store with arbitrary precision. Therefore, today we will talk about how you can implement these procedures, avoiding the above problems. The Galois field theory, which we have already talked about a bit in the last article, will help us in this.
Immediately make a few comments. Firstly, the article is primarily designed for an engineering audience, so I tried to avoid strict mathematical definitions. For those who want a more formal introduction to this area, it makes sense to immediately refer to the relevant literature. For my part, I can recommend Ernest Borisovich Vinberg’s book The Course of Algebra. Second, directly for the implementation of redundant coding algorithms, only a basic understanding of the theory of finite fields is sufficient. You can simply assume that some consistent tables of multiplication, division, addition, subtraction, and all calculations are made using these tables. This is a hint for those who do not really want to dive deep into this section of algebra.
Before proceeding directly to the discussion of the Galois fields, let us repeat once more what we want to achieve. We want to be able to multiply matrices by vectors, to invert matrices. And most importantly, we want to deal only with integers and not worry about overflow when performing multiplication and addition operations.
Also, to avoid confusion, it makes sense to immediately understand the terminology. First of all, what is a field in terms of general algebra? As Wikipedia tells us, “a field is a set for which elements the operations of addition, subtraction, multiplication and division (except division by zero) are defined, and the properties of these operations are close to the properties of ordinary numerical operations.” What is a Galois field? A Galois field is an arbitrary field consisting of a finite number of elements. , - standard designation of Galois fields, where the number of field elements is indicated in brackets.
In modern computers, a fixed number of bits is usually used to store numbers. It is not difficult to calculate that everything exists. different n-bit numbers, from 0 to . In other words, we have some finite set of numbers. On this set, we will now try to determine the operations of multiplication, division, addition, and subtraction in a consistent way. And so that the result of any operation was also bit number! In this case, it is said that the set is closed with respect to the entered operations .
The subtraction operation in systems of finite sets is usually introduced through the concept of zero and opposite elements. Zero element - this is an element for which the equality holds: where Is an arbitrary element of the set. Element is the opposite for if equality is true . Usually the opposite element is denoted as . If we want from subtract we find the opposite element and fold it with . Accordingly, in order to be able to subtract arbitrary elements of a finite set, each element of this set must have the opposite.
Similarly, the situation with the division operation. The concept of single and inverse elements is introduced. Single element Is the element for which the equality is true where Is an arbitrary element of the set. Element (denoted by ) is called the inverse of , if a . As with the subtraction, if we want divide by nonzero we have to find the inverse element and multiply it by . In order to be able to divide arbitrary elements, each element of the set (with the exception of zero) must have the opposite.
How can we determine the specified arithmetic operations on a finite set of numbers, and so that the set is closed with respect to them? In other words, we want an arbitrary finite set of elements to be turned into a Galois field. The first thing that comes to mind is to use modular arithmetic. Then if our set contains elements, the result of the product of numbers will be the number . The sum of the numbers is defined as .
As an exercise, let's create addition and multiplication tables for a set consisting of items .

The lower two tables show the opposite and inverse values for each element of our set. Armed with these tables, we can perform all the arithmetic operations we need. Hooray!
It seems that we are on the right path to success. The only thing that may not suit us so far is the size of our field - 5. It is clear that to simplify the software implementation, it makes sense to work with sets containing numbers Then we can operate with nibbles, bytes, words, etc.
At first glance it seems what a difference - 5 or 256 elements in the set, take the result of the multiplication or addition operation in the corresponding module and is ready. Let's try again to create a multiplication table for the set, but this time containing element - . Here's what happened:

If you look closely at the resulting table, you can find one serious flaw in it. Pay attention to the line for element 2. There is no single element in this line! This means that we will not be able to divide the other elements by 2, since for him there is no opposite! It means that it is necessary to build the tables of addition and multiplication in some other way. Modular arithmetic, unfortunately, no longer works.
So, we found out that if the set contains an object, then modular arithmetic does not allow to set consistent operations of multiplication. In fact, similar problems will arise for any set, the number of elements which is not a prime number. But what else can you think of?
Let us, for the sake of simplicity, assume that the set on which we want to define arithmetic operations contains items. These are, strictly speaking, numbers . Any number of this set can be represented as an expansion:
In essence, this is the usual binary representation of a number. Thus, we can also consider any number from our set as a vector of length whose elements are zeros and ones:
We introduce the operation of adding two arbitrary numbers through the addition of the corresponding vectors of the binary decomposition. Moreover, the addition of the components of the vectors will be modulo 2 (in general, if the number of elements modulo ). Thus, the resulting vector will also be a binary representation of some number and, as a result, will belong to our set (the set will be closed with respect to the addition operation).
It is easy to see that the addition operation we introduced is equivalent to the XOR bit operation. Which is very good, since modern processors can perform this operation extremely quickly. But that is not all. It's obvious that for an arbitrary number . This means that the opposite element to is himself . So in the field addition is the same as subtraction!
It remains to introduce the operation of multiplication on our set. This is done as follows. Let's temporarily assume that any number of our set, it is a polynomial of the following form:
Here the coefficients of the polynomial are taken from the binary decomposition of the number . With this approach, for example, the number the polynomial will be matched .
The multiplication operation of two numbers can be determined by multiplying polynomials corresponding to given numbers:
Moreover, when multiplying all operations with the coefficients of polynomials are performed modulo 2.
But now, obviously, another problem may arise. By multiplying two degree polynomials may turn out to be a higher degree polynomial that will not match any of the numbers in our set. This is solved as follows. An irreducible polynomial of degree is chosen. . Roughly speaking, it is such a polynomial that cannot be represented as a product of other polynomials, more in the article . After this, using the algorithm for dividing polynomials by a column , which many may still remember from the school curriculum, we divide the result of the product into an irreducible polynomial. Once again I remind you that when dividing by a bar, operations with the coefficients of polynomials are also performed modulo 2. As a result, we get a polynomial of degree not higher than which we take for the result of the product of two numbers. Here is an example of performing the multiplication of two numbers over the field using an irreducible polynomial . This polynomial is used in the AES / Rijndael encryption algorithm.
We reviewed the field . Arbitrary fields are built in a similar way, only instead of the binary representation of the number used -personal and all calculations are performed by module .
And what will happen if you choose another irreducible polynomial? You can even put a more general question. Suppose I don’t like all these polynomials and divisions by a bar at all, so I’ll rather think up my own consistent multiplication table using some other principle. Will it be something fundamentally new? The answer is no. All these resulting fields will be isomorphic .
Translating from a "mathematical" language, isomorphism means that the differences are only in the designation of field elements and one can be reduced to another by choosing the appropriate mapping rule.
The finite sets of elements that we have considered so far have been of two types. The first type of set had a number of elements equal to some prime number. . On such sets, we were able to specify the multiplication and addition tables using only modular arithmetic. The second type includes sets that have , - simple number of items. On such sets it is possible to specify multiplication / addition using a scheme with polynomials. Is it possible to specify in a similar way multiplication / addition for sets of arbitrary size, say, containing 6 elements? The answer is no, it is impossible.
Strictly speaking, finite fields are called Galois fields, because he discovered their following important properties:
The second article of the cycle comes to an end. The first two articles presented brief theoretical information related to Reed-Solomon codes and Galois fields. In the next part I plan to elaborate in more detail on the features of the software implementation of the above-mentioned algorithms. Thank.

First, a brief excursion into the last part . We found out that in order to be able to recover lost data, you must first generate “redundant data” in a certain way. Moreover, from a mathematical point of view, this task (coding) is reduced to constructing a certain generating matrix and performing the operation of multiplying this matrix by the vector of the original data. The recovery (decoding) procedure, in turn, consists in inverting the generating matrix and multiplying it by the vector of the preserved data. Schematically it can be represented as follows.
Coding procedure:
')

Decoding procedure:

Limitations of rational number arithmetic
We have already noted some of the difficulties encountered in the implementation of encoding / decoding procedures on specific hardware platforms. For example, numbers in computer memory are usually represented by a fixed number of bytes. As a result, by multiplying the elements of the generating matrix, one can get an overflow of discharges. Or, when the generating matrix is addressed as its elements, rational numbers may arise that are problematic to store with arbitrary precision. Therefore, today we will talk about how you can implement these procedures, avoiding the above problems. The Galois field theory, which we have already talked about a bit in the last article, will help us in this.
Immediately make a few comments. Firstly, the article is primarily designed for an engineering audience, so I tried to avoid strict mathematical definitions. For those who want a more formal introduction to this area, it makes sense to immediately refer to the relevant literature. For my part, I can recommend Ernest Borisovich Vinberg’s book The Course of Algebra. Second, directly for the implementation of redundant coding algorithms, only a basic understanding of the theory of finite fields is sufficient. You can simply assume that some consistent tables of multiplication, division, addition, subtraction, and all calculations are made using these tables. This is a hint for those who do not really want to dive deep into this section of algebra.
Fields and arithmetic operations in finite sets
Before proceeding directly to the discussion of the Galois fields, let us repeat once more what we want to achieve. We want to be able to multiply matrices by vectors, to invert matrices. And most importantly, we want to deal only with integers and not worry about overflow when performing multiplication and addition operations.
Also, to avoid confusion, it makes sense to immediately understand the terminology. First of all, what is a field in terms of general algebra? As Wikipedia tells us, “a field is a set for which elements the operations of addition, subtraction, multiplication and division (except division by zero) are defined, and the properties of these operations are close to the properties of ordinary numerical operations.” What is a Galois field? A Galois field is an arbitrary field consisting of a finite number of elements. , - standard designation of Galois fields, where the number of field elements is indicated in brackets.
In modern computers, a fixed number of bits is usually used to store numbers. It is not difficult to calculate that everything exists. different n-bit numbers, from 0 to . In other words, we have some finite set of numbers. On this set, we will now try to determine the operations of multiplication, division, addition, and subtraction in a consistent way. And so that the result of any operation was also bit number! In this case, it is said that the set is closed with respect to the entered operations .
The subtraction operation in systems of finite sets is usually introduced through the concept of zero and opposite elements. Zero element - this is an element for which the equality holds: where Is an arbitrary element of the set. Element is the opposite for if equality is true . Usually the opposite element is denoted as . If we want from subtract we find the opposite element and fold it with . Accordingly, in order to be able to subtract arbitrary elements of a finite set, each element of this set must have the opposite.
Similarly, the situation with the division operation. The concept of single and inverse elements is introduced. Single element Is the element for which the equality is true where Is an arbitrary element of the set. Element (denoted by ) is called the inverse of , if a . As with the subtraction, if we want divide by nonzero we have to find the inverse element and multiply it by . In order to be able to divide arbitrary elements, each element of the set (with the exception of zero) must have the opposite.
Construction of Galois fields GF (p)
How can we determine the specified arithmetic operations on a finite set of numbers, and so that the set is closed with respect to them? In other words, we want an arbitrary finite set of elements to be turned into a Galois field. The first thing that comes to mind is to use modular arithmetic. Then if our set contains elements, the result of the product of numbers will be the number . The sum of the numbers is defined as .
As an exercise, let's create addition and multiplication tables for a set consisting of items .

The lower two tables show the opposite and inverse values for each element of our set. Armed with these tables, we can perform all the arithmetic operations we need. Hooray!
Building Galois Fields
It seems that we are on the right path to success. The only thing that may not suit us so far is the size of our field - 5. It is clear that to simplify the software implementation, it makes sense to work with sets containing numbers Then we can operate with nibbles, bytes, words, etc.
At first glance it seems what a difference - 5 or 256 elements in the set, take the result of the multiplication or addition operation in the corresponding module and is ready. Let's try again to create a multiplication table for the set, but this time containing element - . Here's what happened:

If you look closely at the resulting table, you can find one serious flaw in it. Pay attention to the line for element 2. There is no single element in this line! This means that we will not be able to divide the other elements by 2, since for him there is no opposite! It means that it is necessary to build the tables of addition and multiplication in some other way. Modular arithmetic, unfortunately, no longer works.
So, we found out that if the set contains an object, then modular arithmetic does not allow to set consistent operations of multiplication. In fact, similar problems will arise for any set, the number of elements which is not a prime number. But what else can you think of?
Addition to GF (p ^ n)
Let us, for the sake of simplicity, assume that the set on which we want to define arithmetic operations contains items. These are, strictly speaking, numbers . Any number of this set can be represented as an expansion:
In essence, this is the usual binary representation of a number. Thus, we can also consider any number from our set as a vector of length whose elements are zeros and ones:
We introduce the operation of adding two arbitrary numbers through the addition of the corresponding vectors of the binary decomposition. Moreover, the addition of the components of the vectors will be modulo 2 (in general, if the number of elements modulo ). Thus, the resulting vector will also be a binary representation of some number and, as a result, will belong to our set (the set will be closed with respect to the addition operation).
It is easy to see that the addition operation we introduced is equivalent to the XOR bit operation. Which is very good, since modern processors can perform this operation extremely quickly. But that is not all. It's obvious that for an arbitrary number . This means that the opposite element to is himself . So in the field addition is the same as subtraction!
Multiplication in GF (p ^ n)
It remains to introduce the operation of multiplication on our set. This is done as follows. Let's temporarily assume that any number of our set, it is a polynomial of the following form:
Here the coefficients of the polynomial are taken from the binary decomposition of the number . With this approach, for example, the number the polynomial will be matched .
The multiplication operation of two numbers can be determined by multiplying polynomials corresponding to given numbers:
Moreover, when multiplying all operations with the coefficients of polynomials are performed modulo 2.
But now, obviously, another problem may arise. By multiplying two degree polynomials may turn out to be a higher degree polynomial that will not match any of the numbers in our set. This is solved as follows. An irreducible polynomial of degree is chosen. . Roughly speaking, it is such a polynomial that cannot be represented as a product of other polynomials, more in the article . After this, using the algorithm for dividing polynomials by a column , which many may still remember from the school curriculum, we divide the result of the product into an irreducible polynomial. Once again I remind you that when dividing by a bar, operations with the coefficients of polynomials are also performed modulo 2. As a result, we get a polynomial of degree not higher than which we take for the result of the product of two numbers. Here is an example of performing the multiplication of two numbers over the field using an irreducible polynomial . This polynomial is used in the AES / Rijndael encryption algorithm.
We reviewed the field . Arbitrary fields are built in a similar way, only instead of the binary representation of the number used -personal and all calculations are performed by module .
Isomorphism of fields and Galois fields of arbitrary size
And what will happen if you choose another irreducible polynomial? You can even put a more general question. Suppose I don’t like all these polynomials and divisions by a bar at all, so I’ll rather think up my own consistent multiplication table using some other principle. Will it be something fundamentally new? The answer is no. All these resulting fields will be isomorphic .
Translating from a "mathematical" language, isomorphism means that the differences are only in the designation of field elements and one can be reduced to another by choosing the appropriate mapping rule.
The finite sets of elements that we have considered so far have been of two types. The first type of set had a number of elements equal to some prime number. . On such sets, we were able to specify the multiplication and addition tables using only modular arithmetic. The second type includes sets that have , - simple number of items. On such sets it is possible to specify multiplication / addition using a scheme with polynomials. Is it possible to specify in a similar way multiplication / addition for sets of arbitrary size, say, containing 6 elements? The answer is no, it is impossible.
Strictly speaking, finite fields are called Galois fields, because he discovered their following important properties:
- The number of elements of the final field is always where prime number as well any kind.
- All size fields isomorphic.
Conclusion
The second article of the cycle comes to an end. The first two articles presented brief theoretical information related to Reed-Solomon codes and Galois fields. In the next part I plan to elaborate in more detail on the features of the software implementation of the above-mentioned algorithms. Thank.
Source: https://habr.com/ru/post/341506/
All Articles