Intuitive algorithm development

If you are a programmer, then perhaps you have a situation where the selected game engine or library does not have the desired function. This was followed by a terrifying moment when you had to search the entire Internet in search of code written by people who solved this problem before you (I’m talking about you, StackOverflow users). Of course, there is nothing wrong with that (I myself do this), but very often you can do it yourself, even when it comes to such theoretical problems as geometry or shuffling. I am one of those people who always try to understand how everything works, and is there really a better way to understand than to come to him himself, reinventing the solution on the fly (if, of course, it exists)?

Set an example task

In this article I will describe several stages, which, it seems to me, are quite effective for self-derivation of the algorithm that solves the problem. To apply them to something concrete, we consider an example of the problem: convex partitioning of simple polygons. It sounds difficult and scientifically, but in fact it is not so difficult.

A simple polygon is a polygon that does not intersect itself and has no holes. A convex polygon is one in which all angles are less than 180 °. Of course, a convex polygon is a simple polygon, and a simple polygon is a complex polygon (the most general class of polygons), but the reverse is not always true.
')

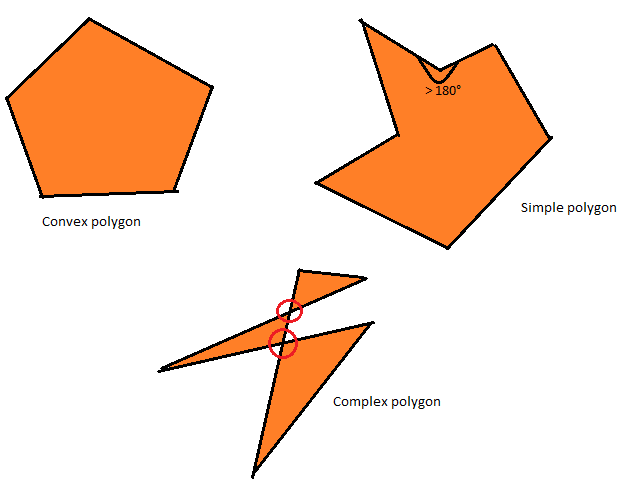
Convex, simple and complex polygons.

A very good property of convex polygons is that checking collisions between two arbitrary convex polygons is very simple (we will not discuss this in the article), while checking collisions between two arbitrary complex, or even simple polygons is indecently complex. And here a convex partition comes into play: if we can divide a simple polygon into several smaller convex polygons, then a collision with it is similar to a collision with at least one polygon from the partition. Therefore, our example of the problem would be as follows: having an array of points describing a simple polygon, return an array of arrays describing convex polygons, “in total” giving the original polygon.


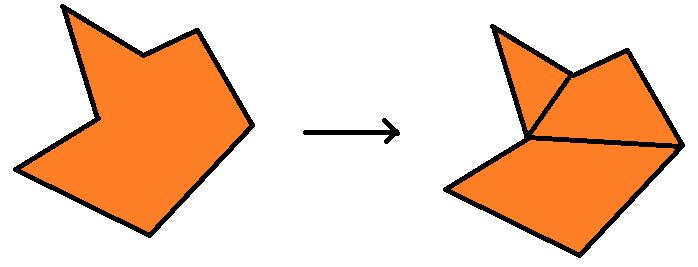
Ideally, our algorithm should be able to perform such an operation.

Learn what you work with

When developing algorithms, the most important thing is to identify the task you want to solve, that is, what the algorithm should do first. It may sound silly, but more important is not how the algorithm should work, but what it should receive at the input and output at the output (including data structures, if necessary). Most often, knowledge of the data structures with which you have to work helps to formulate your reasoning. For example, if you create a sorting algorithm, then there is a chance that it will receive an array at the input, but what should be the output: a new array, nothing or sorting in place (directly changing the source array itself)?

Read my previous article about the algorithm for curves ; this is a good example of an algorithm whose input and output data are rather difficult to characterize. In fact, it can be said that the input algorithm receives a function of a floating-point number and an integer, where the function describes a parametric curve and the integer number describes the number of sampling steps. The algorithm should return at the output another function of a floating-point number, that is, the function of the “curve” to which the article is devoted, and it, in essence, is a more usual version of the original curve.

In our example task, as mentioned above, the algorithm will receive an array of points at the input and return an array of points at the output. The input data will be the vertices of a simple polygon, and the output data will be the vertices of all convex polygons in a convex partition of the original polygon.

First of all - the brain and paper

Starting with paper and pencil (or pens, if you like to take risks) is one of the best ways to perceive a task, and this applies not only to the creation of algorithms (and even not only to programming). Of course, programming is no exception, so let's get started and start from the very beginning.

First, to develop an intuitive approach, it is often best to start with sketching (or writing down, depending on what you are working on) simple cases that you can solve yourself, without really thinking about what you are doing. In the course of this work or after it, you should analyze the way you think about it and organize it, breaking it up into stages. The idea is that, whether you like it or not, you are running an algorithm: your brain is also a computer, the most powerful computer known to man. So powerful that he can look at his own work and understand it; so powerful that you are already performing the algorithm you are trying to write, but for some reason you still do not understand it (because you have not yet realized it!). However, you can run the algorithm step by step to understand how it works. To test this theory, let's go back to our example of the problem and use that simple polygon.

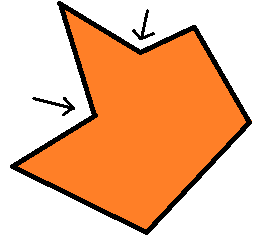
I recommend that you draw such a polygon yourself, and at this moment interrupt reading in order to try to divide this polygon into smaller figures so that they never have internal corners greater than 180 °. I showed my solution in the figure above, but since everyone thinks differently, we may end up with other figures. And this is absolutely normal, in fact, the convex partitioning of a simple polygon is not unique!


Both of these tilings are convex.

After we have applied the algorithm of computational geometry in seconds, without actually knowing it, with the help of the most powerful computer in the known universe, we can turn back and break the algorithm into stages. I repeat, we all think differently, so the stages may differ: I will apply it to my reasoning, and yours will be quite similar.



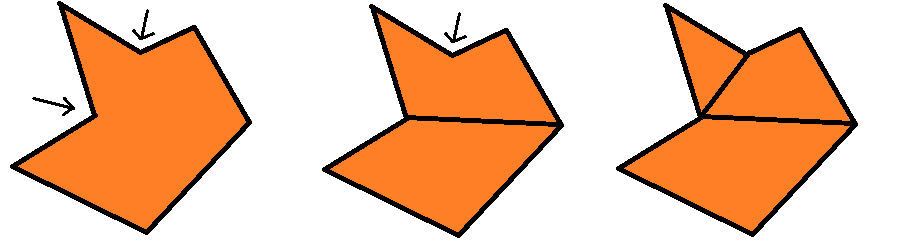
First, I asked myself the question: why is this polygon not yet convex? The answer came rather quickly: because some of the internal angles are greater than 180 ° (namely, two of them, shown in the figure by arrows), which by definition does not allow the polygon to be convex. To fix this, I then thought that I needed to cut an angle to get two smaller angles, which ideally would be no more than 180 °. This can be achieved by connecting the “defective” vertex to some other vertex of the polygon. Repeat this for all defective vertices and get our convex partition!


Stepwise intuitive convex splitting; arrows indicate “defective” vertices.

Well, it all happened pretty quickly. But what really happened? At this stage, we can write the germ of the algorithm in pseudocode that resembles natural language. This is not exactly a sentence from the language, but also not quite programming. It just looks quite similar to programming to run the “think like a programmer” installation in the brain.

  while there is a "defective" vertex
     connect it to another vertex of the polygon
 end bye 

From this, it becomes clear that we need a way to determine if a vertex is "defective." To do this, it is enough just to check whether the two components that form the top of the edge are greater than 180 °. However, there is another, more serious task: which vertex we choose to connect to the defective vertex? Let's think again how we did it last time.

I did it this way: I tried to include as many vertices as possible in each polygon to minimize the number of polygons in the partition. In general, this is a good idea, because it is more efficient to process one rectangle than two triangles, which are connected into a rectangle - although they describe the same shape, we have four vertices in one case and six vertices in the other. We do this as follows: we check each vertex in order, starting with the defective one, until we find the vertex that turns our polygon into a nonconvex one, after which we choose the last vertex in which it remained convex. This is always possible, because the triangle is always convex, so in the worst case we get a triangle. Now our pseudocode will look like this:

  while there is a defective vertex
     while the next vertex forms an angle of 180 ° or less with a defective vertex
         go to the next peak
         if the angle formed by this new vertex is more than 180 °, stop and select the previous
     end bye
     connect the defective vertex with the selected vertex
 end bye 

But this check can lead to a couple of doubtful situations: what if the vertex immediately after our defective vertex is also defective? What if during the verification process we reach the defective vertex? The second question seems to be resolving itself due to the observation that in a convex polygon there can be no defective vertices, it is necessary to immediately stop and choose it so that the edge we add when dividing the angle turns it into the “correct” vertex. The first question can be solved intuitively: when we solve a problem manually, this never happens, because we deliberately start from either the leftmost or the rightmost defective vertex, and obviously not the one that lies between the other defective vertices. In the code, this simply translates into the fact that we start the study from a defective vertex, which exactly has a regular neighbor. This is always possible, because a simple polygon always has at least one “regular” (that is, nondefect) vertex. Find it, use it to get rid of one defective vertex, repeat. Our pseudocode now looks like this:

  while there is a defective vertex
     choose the one after which there is the "right" vertex
     while the next vertex with the defective vertex forms an angle of 180 ° or less
         go to the next peak
         if this new vertex is "wrong", stop and select it
         otherwise, if the angle formed by this new vertex is greater than 180 °, stop and select the previous vertex
     end bye
     connect the defective vertex with the selected vertex
 end bye 

And when executed, the code will give us something like this:


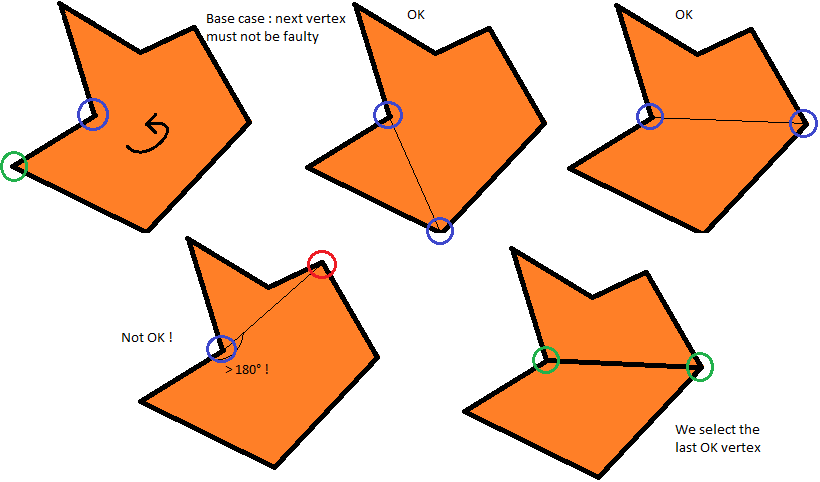
One step of the algorithm: selection of a vertex with which you need to connect a defective vertex.

Looks pretty good!

There is one more question: now we save our polygons as an array of vertices, not edges, what then means “connecting vertices”? We do not add or remove vertices from the polygon, so we probably can’t change the array of vertices? Or can we?

Let's look at how we approached this issue when working manually: after drawing the edge, the part that became convex becomes completely uninteresting, and we focus only on the remaining vertices. However, we are still interested in the newly added edge, and we are still adding to the search its constituent vertices. This has a fairly clear interpretation: we simply split the polygon into two parts, convex and simple, and we no longer care about the convex part when the algorithm is re-applied to a new, smaller simple polygon!



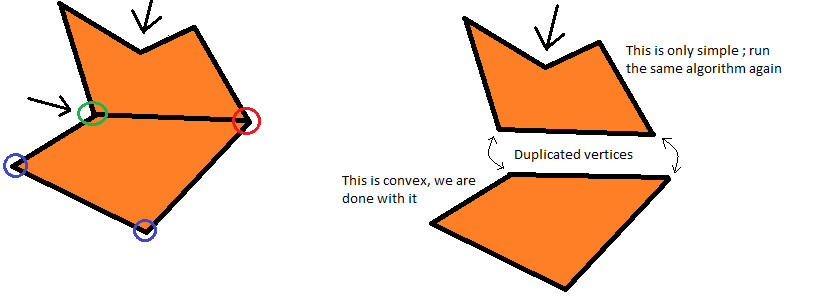
Now we understand what “connecting” means: in essence, this is the creation of a new polygon from all the vertices between the starting and ending points (namely, green and red in the figure; “between” means that we are moving along the polygon) by subtracting this polygon from the original polygon with the repeated call of the algorithm for the resulting smaller group of vertices. Remember that in both polygons there must be both vertices constituting the added edge!

Every time we complete the full iteration of the algorithm and get one convex and one simple parts, we must add the convex part to the array: this is the array that returns the algorithm after its completion, the array of convex components of the original polygon. As for the simple part, then, you guessed it, for her we call the algorithm again.

Now our pseudocode looks like this:

  function makeConvex
     select a defective vertex, after which there is a "correct" vertex
     until the next vertex forms with a defective angle of 180 ° or less
         go to the next peak
         if this new vertex is "wrong", stop and select it
         otherwise, if the angle formed by this new vertex is more than 180 °, stop and select the previous vertex
     end bye
     add to the array all the vertices between the defective vertex and the selected vertex, including both
     remove all vertices between the defective vertex and the selected vertex from the original polygon, not including both
     return the convex array concatenated with the result of the makeConvex function called for the new polygon
 end of function 

And that's all, we are done! Our stage of working with the brain and paper is finished; after this stage, all further work relates to the implementation, so I leave it to you!

Afterword

Do not forget that pseudocode provides a rather naive approach and it is not optimized. The point is not to create the most efficient algorithm, but to learn how to create your own. Think up more and more of your algorithms, and maybe one day you will have the right idea for a smart algorithm that no one else has thought of. If, after reading this article, you decide that before looking for a solution to a specific task online, you should think about creating your own solution, then I will assume that I have achieved my goal.