Works and Copies

This is the fifth article in the series "Theory of Categories for Programmers." The previous articles have already been published on Habré in the translation of Monnoroch :
0. Category Theory for Programmers: Preface
1. Category: essence of composition
2. Types and functions
3. Categories, large and small
4. Categories Claisley

At KDPV, piglet Peter starts one tractor in each category object.

Follow the arrows

Ancient Greek playwright Euripides wrote "Every man is like his environment." This is also true for category theory. You can select a specific category object only by describing the nature of its relationship with other objects (and yourself), where relationships are morphisms.
')
To define objects in terms of their relationships, category theory resorts to the so-called. universal designs . To do this, you can choose a certain pattern, a diagram of objects and morphisms of a certain shape, and consider all the constructions suitable for it in the category under consideration. If the pattern is fairly common and the category is large enough, then it is likely that there will be a lot of constructions found. The idea of ​​a universal construction is to streamline the construction according to some law and choose the most appropriate one.

This process can be compared to a search on the net. User request is our template. If the request is not very specific, then the search system will return a set of suitable documents, only some of which are relevant. To exclude irrelevant answers, the user refines the request, which increases the accuracy of the search. In the end, the search engine ranks matches and, if lucky, the desired result will be at the very top of the list.

Initial (initial) object

The simplest pattern consists of a single object. Obviously, every object of the category fits under it, and there are a lot of them. To select the most suitable, you need to enter a hierarchy on them. The only thing we have is morphisms. If we imagine morphisms as arrows, then it may turn out that a comprehensive chain of arrows extends from one end of the category to the other. This is true in ordered categories, for example, in partial orders. We say that object a precedes object b if there is an arrow (morphism) from a to b . It would be natural to call the initial object that precedes everything else (i.e., there is an arrow from it into any other category object). It is clear that, generally speaking, the initial object may not be. However, it is much worse that there can be more than one objects satisfying the previous definition. How to clarify our definition? The clue is given by ordered categories: there is no more than one arrow between two objects (there is only one way to be more or less than another object). This leads us to the following definition:

The initial object is an object from which exactly one morphism emanates from any category object.

In fact, even such a definition does not guarantee the uniqueness of the initial object (if it exists). However, it guarantees uniqueness up to isomorphism . Isomorphism is a very important concept for category theory, we will return to it soon.

Consider a few examples. The initial object in a partially ordered set is its smallest element. Some partially ordered sets, such as all integers (both positive and negative), do not have an initial object.

In the category of sets, the initial object is the empty set. Recall that the empty set corresponds to the Void type in Haskell (there is no corresponding type in C ++) and the only polymorphic function from Void to any other type called absurd :

 absurd :: Void -> a 

The existence of such a function makes Void initial object of the category of sets.

Terminal object

Let's continue experimenting with a template from a single object, but change the ranking method. We say that the object a follows the object b if there exists a morphism from b to a (pay attention to the change of direction). We are interested in the latest category object. For reasons of uniqueness, we define it like this:

A terminal object is an object into which exactly one morphism comes from any category object.

Again, the terminal object is unique up to isomorphism, which will soon be proved. First, however, consider a few examples. In a partially ordered set, the terminal object (if it exists) is the largest object. In the category of sets, the terminal object is a singleton. Recall that a singleton corresponds to a void type in C ++ and a type () in Haskell and is a type populated by exactly one value, implicit in C ++ and explicit in Haskell, denoted by the same literal () . It was previously established that there is a single pure function from any type in () :

 unit :: a -> () unit _ = () 

so all the requirements for the terminal object are met.

Note that in this case the uniqueness condition is critically important, since there are other sets (in fact, all sets except the empty one) that have incoming morphisms from any other type. For example, there is a function with values ​​of type Bool ( predicate ), defined for any type of argument:

 yes :: a -> Bool yes _ = True 

However, Bool not a terminal object, because there is at least one more function from any type in Bool :

 no :: a -> Bool no _ = False 

The requirement of uniqueness of morphisms gives us the necessary accuracy, narrowing the set of suitable terminal objects to one.

Duality

It is impossible not to notice the symmetry between the definitions of the initial and terminal objects. The whole difference lies in the direction of morphisms. For any category C, you can define a dual category C ^op simply by reversing all the arrows. The dual category automatically satisfies the definition of the category, if we simultaneously redefine the composition together with the reversal of the arrows. If the composition of the original morphisms f::a->b and g::b->c was h::a->c with h=g∘f , then the composition of the inverted morphisms f_op::b->a and g_op::c->b will be h_op::c->a with h_op=f_op∘g_op . Note that the inversion of the identical arrow coincides with itself.

Duality is a very important property of categories, doubling the category-theoretic productivity. For any construction there is a dual one, and by proving one theorem, you get a second one for free. Dual category constructions often have the prefix “co”: works and coproducts, monads and comonads, cones and cocoons, limits and sets, etc. However, it does not make sense to consider co-designs, because the double-facing arrow coincides with the original one, that, for example, kokomonadah coincide with the monad.

So, the terminal object is the initial object in the dual category.

Isomorphisms

Programmers are well aware that determining equality is not so easy. What does it mean that two objects are equal? Should they occupy the same memory area (pointer equality)? Or is it enough that the values ​​of all their components coincide? Are two complex numbers considered equal if one of them is given by the real and imaginary components, and the other by the argument and module? One might hope that mathematicians possess sacred knowledge about the definition of equality, but this is not so. In mathematics, there are also many types of equality, as well as a weaker concept of isomorphism and even weaker equivalence.

Intuitively, objects are isomorphic, if they have the same appearance, are externally indistinguishable: any part of one object is in one-to-one correspondence with some part of another object; according to the readings of the measuring instruments available to us, the objects are exact copies of each other. Mathematically, this means that there are reciprocal mappings from object a to object b and from object b to object a . Category theory generalizes mappings to morphisms. Isomorphism is a reversible morphism or, in other words, a pair of morphisms inverse to each other.

The concept of reversibility is expressed in terms of composition and unitary morphism: the morphism g is inverse to f if their composition is a unit morphism. In fact, this is not one, but two conditions, since there are two ways of composition of a pair of morphisms:

 f . g = id g . f = id 

When we say that the initial (terminal) object is unique up to isomorphism, it means that any two initial (terminal) objects are isomorphic. This is easy to demonstrate. Suppose that i ₁ and i ₂ are initial objects in the same category. Since i _{1 is} initial, there exists a unique morphism f from i ₁ to i ₂ . Similarly, since i _{2 is} initial, there exists a unique morphism g from i ₂ to i ₁ . What can be said about the composition of these morphisms?

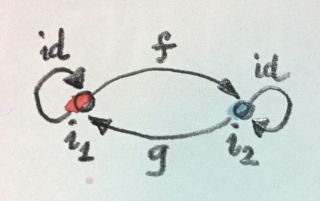
The composition g ∘ f must be a morphism from i ₁ to i ₁ . But i ₁ is the initial object, so that there is exactly one morphism from i ₁ to i ₁ and, since the beginning and end of the arrow are the same, this vacancy is already occupied by a single morphism. Therefore, they must coincide: the morphism g ∘ f is unit. Similarly, the morphism f ∘ g also coincides with the unit one, since there can be only one morphism from i ₂ to i ₂ . Thus, f and g are mutually inverse, and the two initial objects are isomorphic.

Note that our proof of the uniqueness of the initial object up to isomorphism essentially used the uniqueness of the morphism from the initial object to itself. However, is it important that the morphisms f and g are also unique? The fact is that in fact we have proved a more rigorous statement: the initial object is unique up to a unique isomorphism. Generally speaking, there can be more than one isomorphism between two objects, but not in this case. “Uniqueness up to a single isomorphism” is an important feature of all universal constructions.

Artworks

The following universal construction is a work. We are already familiar with the Cartesian product of two sets consisting of the set of all possible pairs. What is the pattern that connects a set-product with sets of factors? If we reveal it, we can generalize the concept of a work to other categories.

Associated with the Cartesian product are two functions ( projectors ) acting from the set-product into the corresponding set factor. In Haskell, these functions are called fst and snd and select the first and second elements of the pair, respectively:

 fst :: (a, b) -> a fst (x, y) = x snd :: (a, b) -> b snd (x, y) = y 

Here, the functions are defined by matching the argument with the pattern: the pattern matches any pair (x, y) and extracts its components into variables x and y .

These definitions can be simplified using dashes:

 fst (x, _) = x snd (_, y) = y 

In C ++, we will use template functions, for example:

 template<class A, class B> A fst(pair<A, B> const & p) { return p.first; } 

With the help of this (seemingly scarce) information about a work, we will try to construct a pattern corresponding to it from objects and morphisms in the category of sets. This pattern will consist of factor objects a and b , object c, and projecting morphisms p and q :

 p :: c -> a q :: c -> b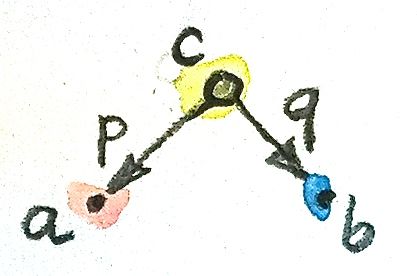 

All objects c that satisfy this pattern will be considered as candidates for the product. There can be a lot of such objects.

As an example, we take two types as factors, namely Int and Bool , and consider a sample of candidates for their work.

Here is the first one: Int . Can Int be considered as a candidate for Int and Bool ? Yes, maybe here are the relevant projectors:

 p :: Int -> Int px = x q :: Int -> Bool q _ = True 

It looks suspicious, but it fits the pattern.

Here is another candidate: (Int, Int, Bool) . This is a tuple of three elements. Here is the corresponding pair of projecting morphisms (we again use pattern matching):

 p :: (Int, Int, Bool) -> Int p (x, _, _) = x q :: (Int, Int, Bool) -> Bool q (_, _, b) = b 

The attentive reader may have noticed that the first candidate is too small - he covers only the Int -component of the work, and the second one is too large, because it includes a clearly fictitious Int -component.

We have so far considered only the first component of the universal design - the template, but did not say anything about the second - about the ranking. We need a way to compare two candidates that match the pattern, namely object c with projectors p and q and object c 'with projectors p ' and q '. I would like to suppose that c is better than c 'if there exists a morphism m from c ' to c , but this is too weak a condition. It is also necessary to require that the projectors p and q be better (more universal) than p 'and q '. This means that p 'and q ' can be reconstructed from p and q with the help of m :

 p' = p . m q' = q . m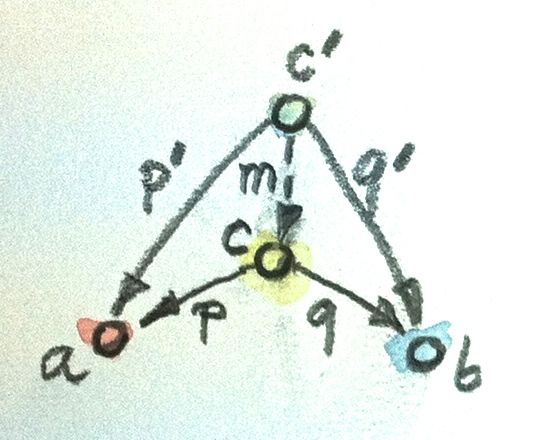 

A number theory expert would say that m is a divisor (factor) of p 'and q '. Imagine natural numbers instead of morphisms and multiplication instead of composition: then m will be a common divisor of p 'and q '. Further in similar situations we will say that m factorizes p 'and q '.

For the training of intuition, we show that a pair (Int, Bool) with two canonical projectors fst and snd definitely better than the candidates discussed above.

The mapping m for the first candidate is:

 m :: Int -> (Int, Bool) mx = (x, True) 

Indeed, both projectors p and q can be reconstructed as:

 px = fst (mx) = x qx = snd (mx) = True 

The morphism m for the second example is also uniquely defined:

 m (x, _, b) = (x, b) 

We showed that (Int, Bool) better than both candidates. We show that the converse is false. Is it possible to find some morphism m' , which will allow to recover fst and snd by p and q ?

 fst = p . m' snd = q . m' 

In the first example, q always returns True , but at the same time there are pairs in which False is the second component. So you can't restore snd by q .

In the second example, things are different: we have enough information after p and q to restore fst and snd , but the factorizing morphism m' is ambiguous. Indeed, since both p and q ignore the second element of the tuple, morphism m' can put anything there:

 m' (x, b) = (x, x, b) 

or

 m' (x, b) = (x, 42, b) 

etc.

Summarizing the above, for a given type c with projectors p and q there exists a unique morphism m from c to the Cartesian product (a, b) , which factorizes p and q . In fact, m simply combines them in a pair:

 m :: c -> (a, b) mx = (px, qx) 

This makes the Cartesian product (a, b) best candidate and completes the consideration of this universal construction for the category of sets.

Now let's forget about the sets and define the product of two objects in an arbitrary category using the same universal construction. Such a product (if exists) is unique up to a unique isomorphism.

The product of objects a and b is such an object equipped with two projectors c , that for any other object equipped with projectors c 'there exists a unique morphism m from c ' to c , factoring these projectors.

The function (higher order) that builds a factorizing morphism on two projectors is sometimes called a factorizer . In our case, it looks like:

 factorizer :: (c -> a) -> (c -> b) -> (c -> (a, b)) factorizer pq = \x -> (px, qx) 

Copies

Like any construction of the theory of categories, the work has a twin called coproduct. If we reverse the arrows in the product template, we obtain an object c , equipped with two embeddings i and j , with morphisms from a and b to c .

 i :: a -> c j :: b -> c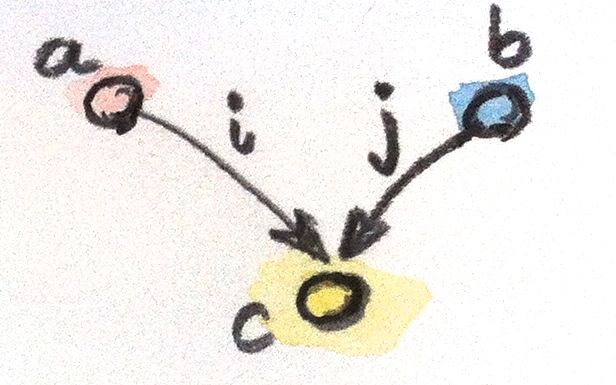 

We also need to reverse the ranking order: now the object c will be considered better than the object c ', equipped with the attachments i ' and j ', if there exists a morphism m from c to c ', which factorizes the attachments:

 i' = m . i j' = m . j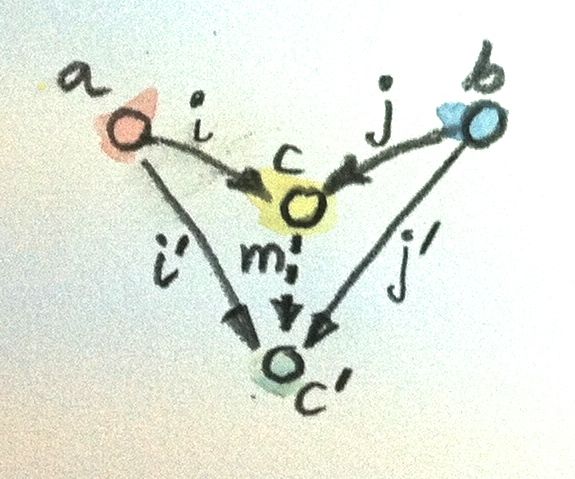 

The best of such objects, possessing a unique morphism into all other objects that correspond to a pattern, is called coproduct and, if it exists, is unique up to a single isomorphism.

The copying of objects a and b is an object c equipped with two embeddings, such that for any other object equipped with embeddings c ', there exists a unique morphism m from c to c ' that factorizes these embeddings.

In the category of sets, coproduct is a disjoint union . The element of the disjoint union a and b is either the element a or the element b . If two sets intersect, then the disjoint union contains both copies of the common part. The elements of a disjoint union can be considered labeled as source sets.

For a programmer, coproduct is a marked union of two types. C ++ supports unlabeled unions; the task of tracking which member of the union is valid lies on the programmer’s shoulders. To create a tagged union, you need to define a label - an enumeration - and combine it with the union. For example, the marked union int and char const * might look like this:

 struct Contact { enum { isPhone, isEmail } tag; union { int phoneNum; char const * emailAddr; }; }; 

Two attachments can be implemented either as constructors or as functions. For example, here is the first attachment as a PhoneNum function:

 Contact PhoneNum(int n) { Contact c; c.tag = isPhone; c.phoneNum = n; return c; } 

This function inserts an int into Contact .

Marked union is also called variant , the generalized implementation of which is in the boost library ( boost::variant ).

In Haskell, you can make a tagged union of any data types by separating the constructors with a vertical bar. The above Contact written as:

 data Contact = PhoneNum Int | EmailAddr String 

Here, PhoneNum and EmailAddr serve both as constructors (attachments) and as labels for pattern matching (see below). For example, this is how you can build Contact by phone number:

 helpdesk :: Contact; helpdesk = PhoneNum 2222222 

Unlike the canonical implementation of the work, embedded in Haskell syntax as a primitive pair, the canonical implementation of coproduct is not a special language construct, but an ordinary data type Either from the standard library:

 Either ab = Left a | Right b 

This data type is parametrized by two types a and b and has two constructors: Left , which accepts type a , and Right , which accepts type b .

By analogy with the factorizer for the product, the factorizer for the coproduct can also be defined. For a given candidate for coproduction in the form of type c with two embeddings i and j we construct a factorizing morphism:

 factorizer :: (a -> c) -> (b -> c) -> Either ab -> c factorizer ij (Left a) = ia factorizer ij (Right b) = jb 

Asymmetry

Above, we considered two pairs of dual definitions: first, the definition of a terminal object can be obtained from the definition of the initial object by reversing the arrows, secondly, the definition of coproduct from the definition of work is obtained in the same way. However, in the category of sets, the initial object is fundamentally different from the terminal one, and the coproduct is different from the product. Below it will be shown that the product behaves as an multiplication with a terminal object playing the role of a unit, and coproduct is similar to addition, where instead of zero it is the initial object. In particular, for finite sets, the number of elements in the product is the product of the numbers of elements in the original sets, and the number of elements in the coproduct is equal to the sum of the original quantities.

This shows that the category of sets is not symmetric with respect to the inversion of arrows.

Note that despite the fact that a single arrow emanates from any empty set into any other set (the absurd function), there is not a single morphism included in it. A singleton (a set of one element) has not only a single arrow entering into it from any set, but also outgoing arrows into each non-empty set. As we saw earlier, these arrows outgoing from the terminal object play an important role in the choice of elements of other sets (there are no elements in the empty set, so there is nothing to choose).

A relationship with a singleton is what distinguishes a piece from a coproduct. Consider a singleton consisting of a single element () as an object that corresponds to the product pattern. We equip it with two projectors: let p and q be functions from a singleton to each of the components of the product. Both of them choose fixed elements in the corresponding sets. Since the product is universal, there exists a (unique) morphism m from a singleton to a product. This morphism selects an element from the set of the product, that is, a fixed pair, and factorizes the projectors:

 p = fst . m q = snd . m 

If we substitute the single element of singleton () into these equations, we get:

 p () = fst (m ()) q () = snd (m ()) 

Since m () is an element of the product chosen by the morphism m , these equations mean that the element p () chosen by the projector p from the first set is the first component of the pair chosen by m . Similarly, q () is equal to the second component. This is fully consistent with the interpretation of the elements of the set-product as pairs of elements from the multipliers.

However, for such a copy, such a simple interpretation does not exist. , , , . ( , , ). . ( ) ( ).

; , Set . . .

( ), . , . — . , , .

, . , () . unit . , .

, , . . , . , , . — , .

1. , .
2. ? : .
3. ?
4. Either Haskell ( Haskell).
5. Show what Eitheris more appropriate to copy than int, equipped with two attachments:
   

    int i(int n) { return n; } int j(bool b) { return b ? 0 : 1; } 

   
   Hint: define function
   

    int m(Either const & e); 

   
   which factorizes iand j.
6. (Continued) Argue why intwith two attachments iand jmay not be preferable Either?
7. (Continued) How about such an investment?
   

    int i(int n) { if (n < 0) return n; return n + 2; } int j(bool b) { return b ? 0 : 1; } 

8. Offer the unsuccessful candidate for coproducts for intand bool, which will be worse Eitherbecause it allows several morphisms in Either.

Literature

The Catsters, Products and Coproducts video.

Thanks

The author is grateful to Gershom Bazerman for reviewing the post before publication and fruitful discussions.