Equivalent transformations of Maxwell equations (ps)
The topic is purely technical, concerning only the issues of processing the data of calculations of electrodynamics, a lot of formulas.
§Potentials (vectors) Hertz
In electrodynamics, in addition to electric potentials, there are Hertz vectors, which are sometimes used to calculate radiation due to (not) a large defect - do not take into account (or weakly) matter. Let's try to enter otherwise:
(remark: if it is very important, namely, their ethodynamic description / use, you can take a look: V. Panovsky & M. Phillips “Classical Electrodynamics.” ISBN: 978-5-9775-0343-3)
')
(clarification: electrodynamics is a phenomenological theory only in integral form, or in simple language, differential equations of ED are possible only over operators / generalized functions in smooth / piecewise smooth metric fields, but are further used in the differential formulation of ED, only for simplicity and clarity, and you need to take into account this clarification.)
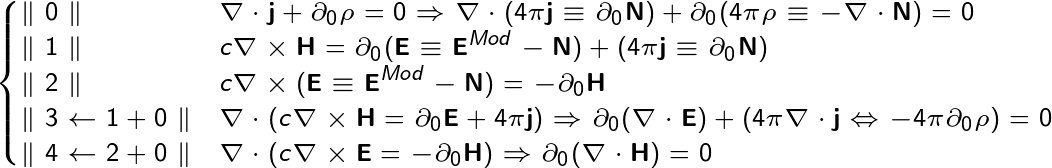
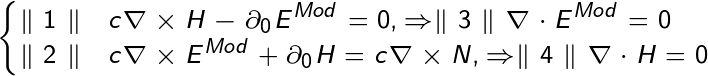
- what is z0 ?! This non-electrodynamic phenomenon, not matter and not radiation, has neither beginning nor end (in our Universe there are no its charges, and either a closed field, or goes beyond infinity), but it can interact with electromagnetic charges ...
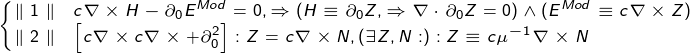
There are two possible interpretations: the first is with the substance, the second is without it
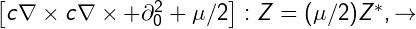
- ... it may be necessary to use a different designation, but stopped at 'Z' (in some sources, the Hertz vector is so designated, although here both potentials are together).
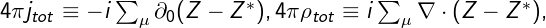
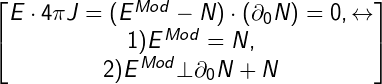
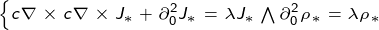
- from the features of these spectra it follows that time separation is possible ...
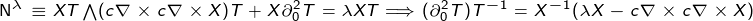
further it will be clear that (until something strongly operative and specific is found) only the case \ omega = 1 is possible ...
But while one trick, which was overseen by Saks Romen Semenovich , you can also read the motivation ...
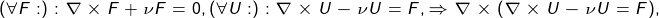
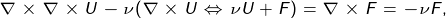
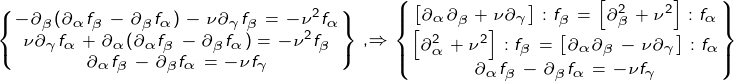
- selecting a couple of functions, the third depends on them ...
or so ...
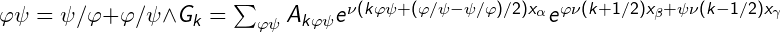
- it can be interesting only in order to assess the forming ...
... but, as I see it, this is too dlllllinny way, there are more direct:
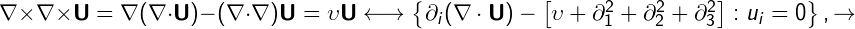
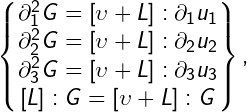
There are three options:
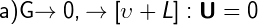- divergence is zero - it is not a substance. But it can be assumed that there is a substance with radiation properties, sometimes locally violating the principle of causality, as the Dirac delta function.
- by choosing 'G', you can complete the field.
But the system of lim [L] :( v div G) -> 0 and lim [Lv]: G -> 0, i.e. lim v * v * div: G -> 0 hints that it is not exactly matter, v is the basis of the Grassmann algebra, G is the solution of the homogeneous Helmholtz equation in this algebra?
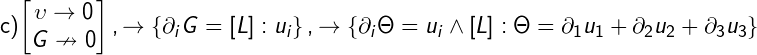- the most interesting option.
*** Some carriers:
sin / sinh
sin / sinh ^ (3/2)
sin * ln (sin)
sin ^ (1/2) * ln (sin)
§Amateur SI units
- this is equivalent to the first system "symmetric form", there are no questions?
Wikipedia and especially pay attention to D.V. Sivukhin
In the textbook: Vlasov AD and Murin B.P. “Units of physical quantities in science and technology. Reference book. ISBN 5-283-03966-8 1990
From page 139, various scales / units are given, and you can independently “play around” with the dimensions.
§Potentials (vectors) Hertz
In electrodynamics, in addition to electric potentials, there are Hertz vectors, which are sometimes used to calculate radiation due to (not) a large defect - do not take into account (or weakly) matter. Let's try to enter otherwise:
(remark: if it is very important, namely, their ethodynamic description / use, you can take a look: V. Panovsky & M. Phillips “Classical Electrodynamics.” ISBN: 978-5-9775-0343-3)
')
(clarification: electrodynamics is a phenomenological theory only in integral form, or in simple language, differential equations of ED are possible only over operators / generalized functions in smooth / piecewise smooth metric fields, but are further used in the differential formulation of ED, only for simplicity and clarity, and you need to take into account this clarification.)
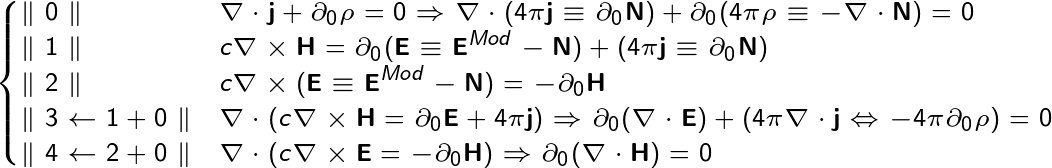
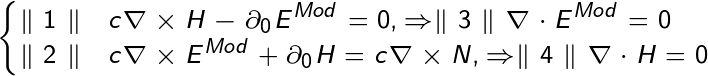
- what is z0 ?! This non-electrodynamic phenomenon, not matter and not radiation, has neither beginning nor end (in our Universe there are no its charges, and either a closed field, or goes beyond infinity), but it can interact with electromagnetic charges ...
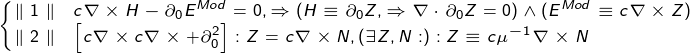
There are two possible interpretations: the first is with the substance, the second is without it
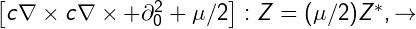
- ... it may be necessary to use a different designation, but stopped at 'Z' (in some sources, the Hertz vector is so designated, although here both potentials are together).
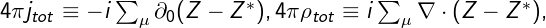
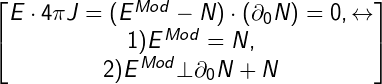
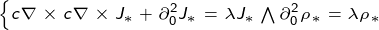
- from the features of these spectra it follows that time separation is possible ...
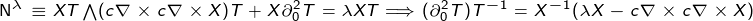
further it will be clear that (until something strongly operative and specific is found) only the case \ omega = 1 is possible ...
But while one trick, which was overseen by Saks Romen Semenovich , you can also read the motivation ...
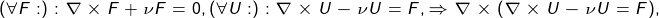
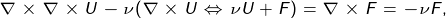
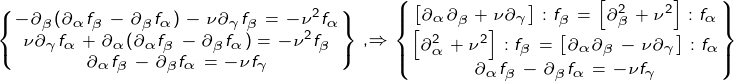
- selecting a couple of functions, the third depends on them ...
or so ...
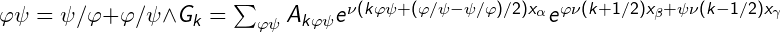
- it can be interesting only in order to assess the forming ...
... but, as I see it, this is too dlllllinny way, there are more direct:
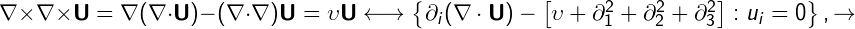
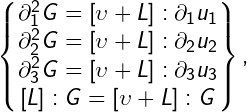
There are three options:
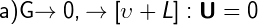- divergence is zero - it is not a substance. But it can be assumed that there is a substance with radiation properties, sometimes locally violating the principle of causality, as the Dirac delta function. - by choosing 'G', you can complete the field.But the system of lim [L] :( v div G) -> 0 and lim [Lv]: G -> 0, i.e. lim v * v * div: G -> 0 hints that it is not exactly matter, v is the basis of the Grassmann algebra, G is the solution of the homogeneous Helmholtz equation in this algebra?
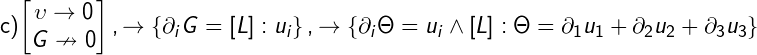- the most interesting option.*** Some carriers:
sin / sinh
sin / sinh ^ (3/2)
sin * ln (sin)
sin ^ (1/2) * ln (sin)
§Amateur SI units
- this is equivalent to the first system "symmetric form", there are no questions?Wikipedia and especially pay attention to D.V. Sivukhin
In the textbook: Vlasov AD and Murin B.P. “Units of physical quantities in science and technology. Reference book. ISBN 5-283-03966-8 1990
From page 139, various scales / units are given, and you can independently “play around” with the dimensions.
If someone needs in the format LaTeX ...
$ \ begin {cases}
\ parallel0 \ parallel & \ nabla \ cdot \ mathbf {j} + \ partial_ {0} \ rho = 0 \ Rightarrow \ nabla \ cdot (4 \ pi \ mathbf {j} \ equiv \ partial_ {0} \ mathbf {N }) + \ partial_ {0} (4 \ pi \ rho \ equiv- \ nabla \ cdot \ mathbf {N}) = 0 \\
\ parallel1 \ parallel & c \ nabla \ times \ mathbf {H} = \ partial_ {0} (\ mathbf {E} \ equiv \ mathbf {E} ^ {Mod} - \ mathbf {N}) + (4 \ pi \ mathbf {j} \ equiv \ partial_ {0} \ mathbf {N}) \\
\ parallel2 \ parallel & c \ nabla \ times (\ mathbf {E} \ equiv \ mathbf {E} ^ {Mod} - \ mathbf {N}) = - \ partial_ {0} \ mathbf {H} \\
\ parallel3 \ leftarrow1 + 0 \ parallel & \ nabla \ cdot (c \ nabla \ times \ mathbf {H} = \ partial_ {0} \ mathbf {E} +4 \ pi \ mathbf {j}) \ Rightarrow \ partial_ { 0} (\ nabla \ cdot \ mathbf {E}) + (4 \ pi \ nabla \ cdot \ mathbf {j} \ Leftrightarrow-4 \ pi \ partial_ {0} \ rho) = 0 \\
\ parallel4 \ leftarrow2 + 0 \ parallel & \ nabla \ cdot (c \ nabla \ times \ mathbf {E} = - \ partial_ {0} \ mathbf {H}) \ Rightarrow \ partial_ {0} (\ nabla \ cdot \ mathbf {H}) = 0
\ end {cases} $
$ \ begin {cases}
\ parallel1 \ parallel & c \ nabla \ times H- \ partial_ {0} E ^ {Mod} = 0, \ Rightarrow \ parallel3 \ parallel \ nabla \ cdot E ^ {Mod} = 0 \\
\ parallel2 \ parallel & c \ nabla \ times E ^ {Mod} + \ partial_ {0} H = c \ nabla \ times N, \ Rightarrow \ parallel4 \ parallel \ nabla \ cdot H = 0
\ end {cases} $
$ \ begin {cases}
\ parallel2_ {0} \ parallel & c \ nabla \ times E ^ {Mod} + \ partial_ {0} H = 0, \ Rightarrow (E_ {0} ^ {Mod} \ equiv- \ partial_ {0} z_ {0 }) \ wedge (H_ {0} \ equiv c \ nabla \ times z_ {0}) \\
\ parallel1_ {0} \ parallel & c \ nabla \ times H- \ partial_ {0} E ^ {Mod} = 0, \ Rightarrow (\ forall z_ {0}) :: \ left [c \ nabla \ times c \ nabla \ times + \ partial_ {0} ^ {2} \ right]: z_ {0} = 0 \\
\ parallel3` \ parallel & \ nabla \ cdot E ^ {Mod} = 0 \ Rightarrow \ nabla \ cdot (- \ partial_ {0} z_ {0}) = 0, \ Rightarrow (\ forall z_ {0}) :: \ left [\ partial_ {0} ^ {2} -c ^ {2} \ nabla ^ {2} \ right]: z_ {0} = 0
\ end {cases} $
$ \ begin {cases}
\ parallel1 \ parallel & c \ nabla \ times H- \ partial_ {0} E ^ {Mod} = 0, \ Rightarrow (H \ equiv \ partial_ {0} Z, \ Rightarrow \ nabla \ cdot \ partial_ {0} Z = 0) \ wedge (E ^ {Mod} \ equiv c \ nabla \ times Z) \\
\ parallel2 \ parallel & \ left [c \ nabla \ times c \ nabla \ times + \ partial_ {0} ^ {2} \ right]: Z = c \ nabla \ times N, (\ exists Z, N :): Z \ equiv \ frac {1} {\ mu} c \ nabla \ times N
\ end {cases} $
$ \ begin {cases}
\ parallel N \ parallel & (\ forall N:): \ left [c \ nabla \ times c \ nabla \ times + \ partial_ {0} ^ {2} - \ mu \ right]: N = 0, \ Rightarrow H_ { \ mu} = \ frac {c} {\ mu} \ partial_ {0} \ nabla \ times N + c \ nabla \ times z_ {0} \ wedge E _ {\ mu} ^ {Mod} \ equiv \ frac {c } {\ mu} \ nabla \ times c \ nabla \ times N- \ partial_ {0} z_ {0} \\
\ parallel N` \ parallel & (\ forall N`:): \ left [\ partial_ {0} ^ {2} -c ^ {2} \ nabla ^ {2} - \ mu \ right]: N` = 0
\ end {cases} $
$ Z \ equiv z_ {0} / 2 + iN / 2, \ Rightarrow \ left [c \ nabla \ times c \ nabla \ times + \ partial_ {0} ^ {2} \ right]: Z = i \ mu N / 2 = - \ mu (ZZ ^ {*}) / 2, \ rightarrow $
$ \ left [c \ nabla \ times c \ nabla \ times + \ partial_ {0} ^ {2} + i \ mu / 2 \ right]: Z = i (\ mu / 2) Z ^ {*}, \ rightarrow $
$ 4 \ pi j \ equiv-i \ partial_ {0} (ZZ ^ {*}), 4 \ pi \ rho \ equiv i \ nabla \ cdot (ZZ ^ {*}), $
$ H _ {\ mu} \ equiv-ic \ mu ^ {- 1} \ partial_ {0} \ nabla \ times (ZZ ^ {*}) + c \ nabla \ times (Z + Z ^ {*}), $
$ E _ {\ mu} \ equiv-ic \ mu ^ {- 1} \ nabla \ times c \ nabla \ times (ZZ ^ {*}) + i (ZZ ^ {*}) - \ partial_ {0} (Z + Z ^ {*}) $
\ parallel0 \ parallel & \ nabla \ cdot \ mathbf {j} + \ partial_ {0} \ rho = 0 \ Rightarrow \ nabla \ cdot (4 \ pi \ mathbf {j} \ equiv \ partial_ {0} \ mathbf {N }) + \ partial_ {0} (4 \ pi \ rho \ equiv- \ nabla \ cdot \ mathbf {N}) = 0 \\
\ parallel1 \ parallel & c \ nabla \ times \ mathbf {H} = \ partial_ {0} (\ mathbf {E} \ equiv \ mathbf {E} ^ {Mod} - \ mathbf {N}) + (4 \ pi \ mathbf {j} \ equiv \ partial_ {0} \ mathbf {N}) \\
\ parallel2 \ parallel & c \ nabla \ times (\ mathbf {E} \ equiv \ mathbf {E} ^ {Mod} - \ mathbf {N}) = - \ partial_ {0} \ mathbf {H} \\
\ parallel3 \ leftarrow1 + 0 \ parallel & \ nabla \ cdot (c \ nabla \ times \ mathbf {H} = \ partial_ {0} \ mathbf {E} +4 \ pi \ mathbf {j}) \ Rightarrow \ partial_ { 0} (\ nabla \ cdot \ mathbf {E}) + (4 \ pi \ nabla \ cdot \ mathbf {j} \ Leftrightarrow-4 \ pi \ partial_ {0} \ rho) = 0 \\
\ parallel4 \ leftarrow2 + 0 \ parallel & \ nabla \ cdot (c \ nabla \ times \ mathbf {E} = - \ partial_ {0} \ mathbf {H}) \ Rightarrow \ partial_ {0} (\ nabla \ cdot \ mathbf {H}) = 0
\ end {cases} $
$ \ begin {cases}
\ parallel1 \ parallel & c \ nabla \ times H- \ partial_ {0} E ^ {Mod} = 0, \ Rightarrow \ parallel3 \ parallel \ nabla \ cdot E ^ {Mod} = 0 \\
\ parallel2 \ parallel & c \ nabla \ times E ^ {Mod} + \ partial_ {0} H = c \ nabla \ times N, \ Rightarrow \ parallel4 \ parallel \ nabla \ cdot H = 0
\ end {cases} $
$ \ begin {cases}
\ parallel2_ {0} \ parallel & c \ nabla \ times E ^ {Mod} + \ partial_ {0} H = 0, \ Rightarrow (E_ {0} ^ {Mod} \ equiv- \ partial_ {0} z_ {0 }) \ wedge (H_ {0} \ equiv c \ nabla \ times z_ {0}) \\
\ parallel1_ {0} \ parallel & c \ nabla \ times H- \ partial_ {0} E ^ {Mod} = 0, \ Rightarrow (\ forall z_ {0}) :: \ left [c \ nabla \ times c \ nabla \ times + \ partial_ {0} ^ {2} \ right]: z_ {0} = 0 \\
\ parallel3` \ parallel & \ nabla \ cdot E ^ {Mod} = 0 \ Rightarrow \ nabla \ cdot (- \ partial_ {0} z_ {0}) = 0, \ Rightarrow (\ forall z_ {0}) :: \ left [\ partial_ {0} ^ {2} -c ^ {2} \ nabla ^ {2} \ right]: z_ {0} = 0
\ end {cases} $
$ \ begin {cases}
\ parallel1 \ parallel & c \ nabla \ times H- \ partial_ {0} E ^ {Mod} = 0, \ Rightarrow (H \ equiv \ partial_ {0} Z, \ Rightarrow \ nabla \ cdot \ partial_ {0} Z = 0) \ wedge (E ^ {Mod} \ equiv c \ nabla \ times Z) \\
\ parallel2 \ parallel & \ left [c \ nabla \ times c \ nabla \ times + \ partial_ {0} ^ {2} \ right]: Z = c \ nabla \ times N, (\ exists Z, N :): Z \ equiv \ frac {1} {\ mu} c \ nabla \ times N
\ end {cases} $
$ \ begin {cases}
\ parallel N \ parallel & (\ forall N:): \ left [c \ nabla \ times c \ nabla \ times + \ partial_ {0} ^ {2} - \ mu \ right]: N = 0, \ Rightarrow H_ { \ mu} = \ frac {c} {\ mu} \ partial_ {0} \ nabla \ times N + c \ nabla \ times z_ {0} \ wedge E _ {\ mu} ^ {Mod} \ equiv \ frac {c } {\ mu} \ nabla \ times c \ nabla \ times N- \ partial_ {0} z_ {0} \\
\ parallel N` \ parallel & (\ forall N`:): \ left [\ partial_ {0} ^ {2} -c ^ {2} \ nabla ^ {2} - \ mu \ right]: N` = 0
\ end {cases} $
$ Z \ equiv z_ {0} / 2 + iN / 2, \ Rightarrow \ left [c \ nabla \ times c \ nabla \ times + \ partial_ {0} ^ {2} \ right]: Z = i \ mu N / 2 = - \ mu (ZZ ^ {*}) / 2, \ rightarrow $
$ \ left [c \ nabla \ times c \ nabla \ times + \ partial_ {0} ^ {2} + i \ mu / 2 \ right]: Z = i (\ mu / 2) Z ^ {*}, \ rightarrow $
$ 4 \ pi j \ equiv-i \ partial_ {0} (ZZ ^ {*}), 4 \ pi \ rho \ equiv i \ nabla \ cdot (ZZ ^ {*}), $
$ H _ {\ mu} \ equiv-ic \ mu ^ {- 1} \ partial_ {0} \ nabla \ times (ZZ ^ {*}) + c \ nabla \ times (Z + Z ^ {*}), $
$ E _ {\ mu} \ equiv-ic \ mu ^ {- 1} \ nabla \ times c \ nabla \ times (ZZ ^ {*}) + i (ZZ ^ {*}) - \ partial_ {0} (Z + Z ^ {*}) $
Source: https://habr.com/ru/post/271911/
All Articles