We solve the problem of finding the length of the largest increasing subsequence

Content:

Fibonacci sequence O (n)
Solution for O (n ^ 2)
Binary search O (log n)
Solution for O (n * log n)

Task

"Find the length of the longest increasing subsequence in the array."

In general, this is a special case of the problem of finding common elements of 2 sequences, where the second sequence is the same sequence, only sorted.

On fingers

There is a sequence:

5, 10, 6, 12, 3, 24, 7, 8

Here are examples of subsequences:

10, 3, 8
5, 6, 3

Here are examples of increasing subsequences:

5, 6, 7, 8
3, 7, 8

Here are examples of increasing subsequences of the greatest length:

5, 6, 12, 24
5, 6, 7, 8

Yes, there can be a lot of maximums too, we are only interested in length.
Here it is 4.

Now that the task is defined, we begin to solve it with (surprise!) Calculating Fibonacci numbers, because computing them is the simplest algorithm that uses “dynamic programming”. DP is a term that personally does not cause any correct associations in me, I would call this approach like this - “Programming with preserving the intermediate result of the same task, but of smaller dimensionality”. If, on the other hand, calculating Fibonacci numbers with the help of PD is easier for you than a folded turnip - safely proceed to the next part. The Fibonacci numbers themselves are not related to the original subsequence problem, I just want to show the principle of the DP.

Fibonacci sequence O (n)

The Fibonacci sequence is popular and surrounded by legends, trying to see it (and I must admit, they succeed ) wherever possible. Its principle is simple. The n-th element of the sequence is equal to the sum of the n-1 and n-2 elements. Begins respectively with 0 and 1.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ...

Take 0, add 1 - we get 1.
Take 1, add 1 - we get 2.
We take 1, we add 2 - we get, well, you understand, 3.

Actually finding the nth element of this sequence will be our task. The solution lies in the very definition of this sequence. We will create one mutable array in which we will save intermediate results of calculating Fibonacci numbers, i.e. those n-1 and n-2.

Pseudocode:

int numberForIndex(int index) { int[] numbers = [0, 1]; //  ,      for (int i = 2; i < index + 1; i++) { numbers[index] = numbers[i - 1] + numbers[i - 2]; } return numbers[index]; } 

→ Objective-C Solution Example

→ Tests

That's all, in this numbers array, the entire salt of the DP is a kind of cache (Cahe), into which we add the previous results of the calculation of the same problem, only on a smaller dimension (n-1 and n-2), which gives us the opportunity for one action is to find a solution for dimension n.

This algorithm works for O (n), but uses a little extra memory — our array.

Let us return to finding the length of the maximum increasing subsequence.

Solution for O (n ^ 2)

Consider the following increasing subsequence:

5, 6, 12

Now take a look at the next number after the last element in the sequence - it is 3.

Could it be a continuation of our sequence? Not. It is less than 12.

And 24?

It yes, it can.

Accordingly, the length of our sequence is now equal to 3 + 1, and the sequence looks like this:

5, 6, 12, 24

Here is the reuse of the previous calculations: we know that we have a subsequence of 5, 6, 12, which has a length of 3 and now we can easily add to it 24. Now you have the feeling that we can use it, just how?

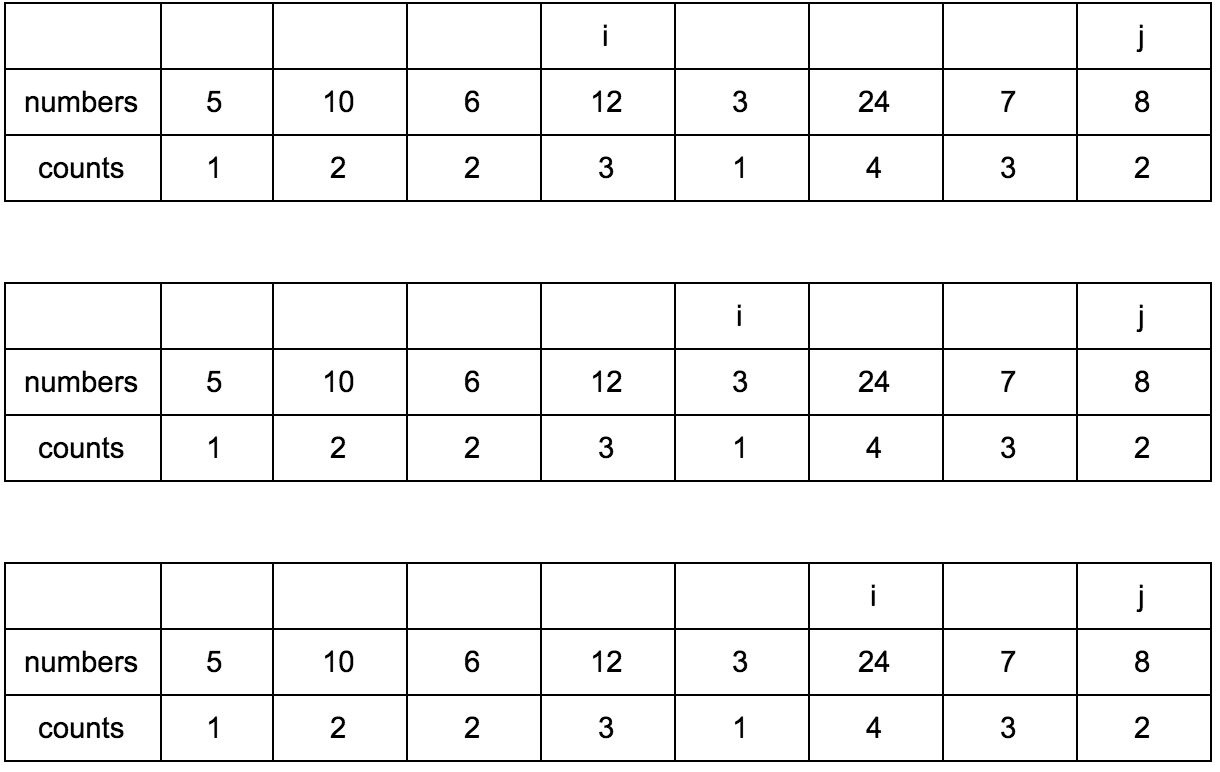
Let's create another additional array (here it is our cache, here it is our DP), in which we will store the size of the increasing subsequence for the nth element.

It will look like this:

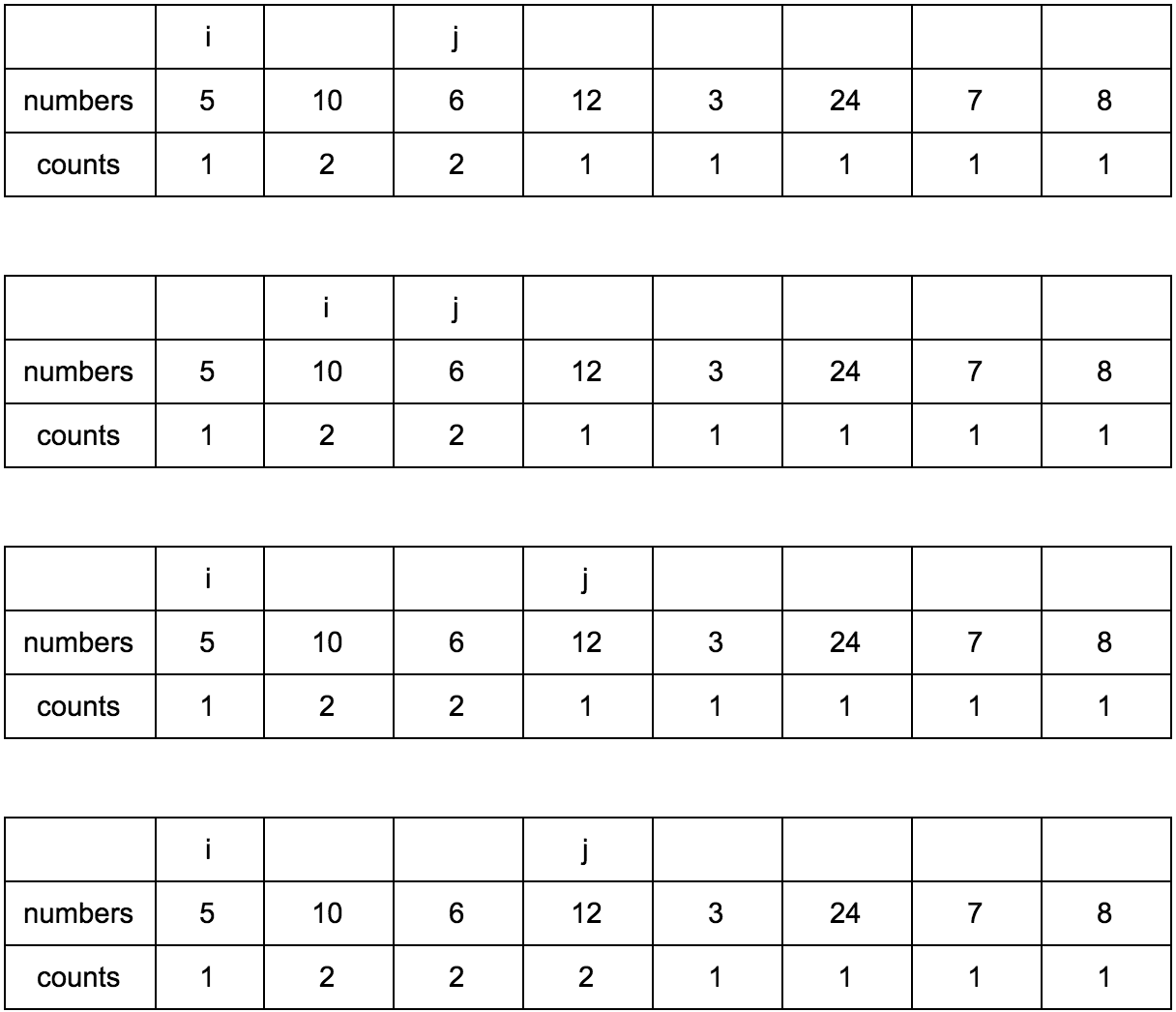
Our task is to fill the counts array with the correct values. Initially, it is filled with units, since each element in itself is a minimal increasing subsequence.

“What are the mysterious i and j?” - you ask. These are indices of iterators over the array that we will use. They will be changed using two cycles, one in the other. i will always be less than j.

Now j is looking at 10 - this is our candidate member of the sequences that go to him. Let's see where i is, there stands 5.

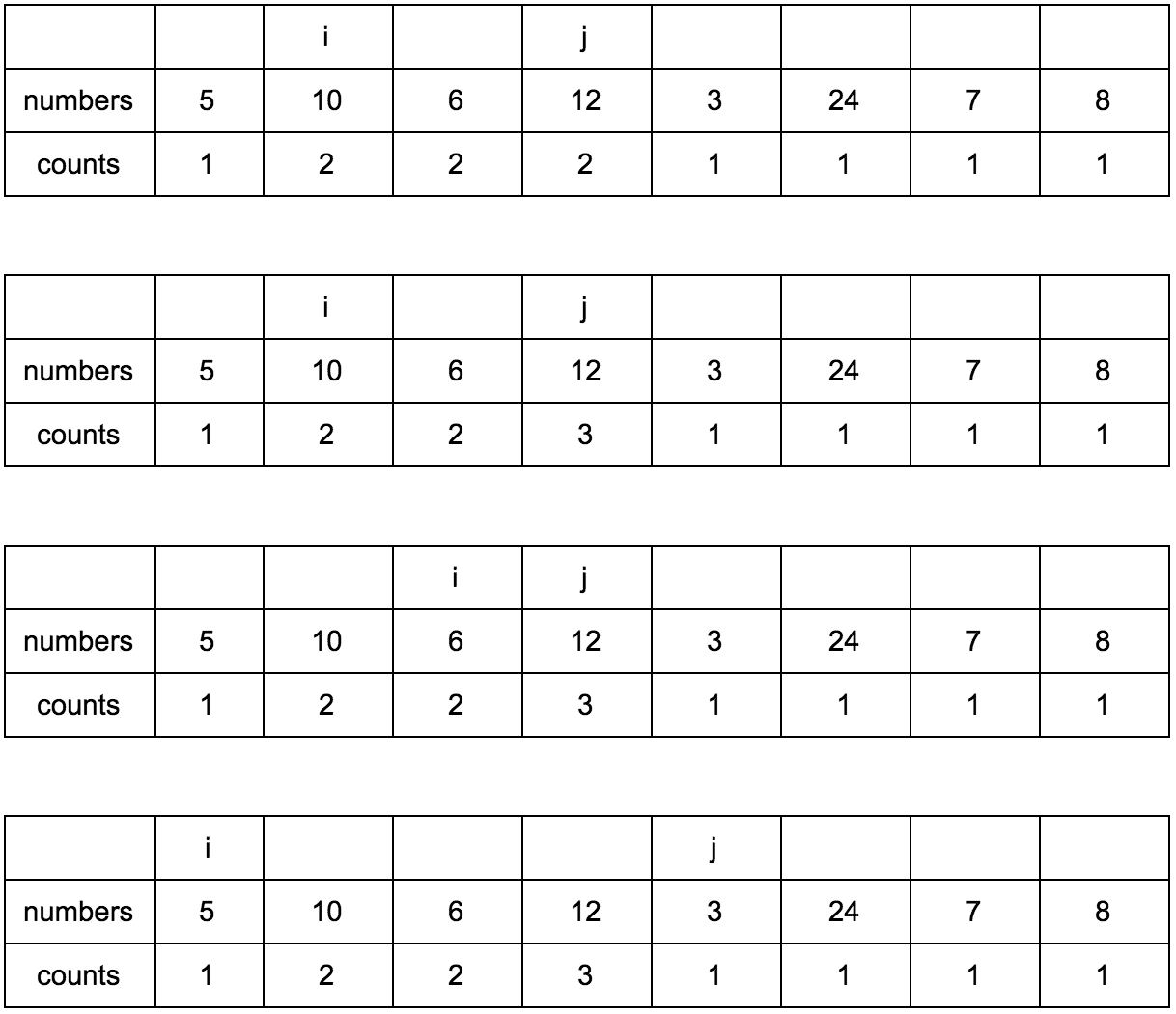
10 over 5 and 1 <= 1, counts [j] <= counts [i]? Yes, it means counts [j] = counts [i] + 1, remember our reasoning at the beginning?

Now the table looks like this.

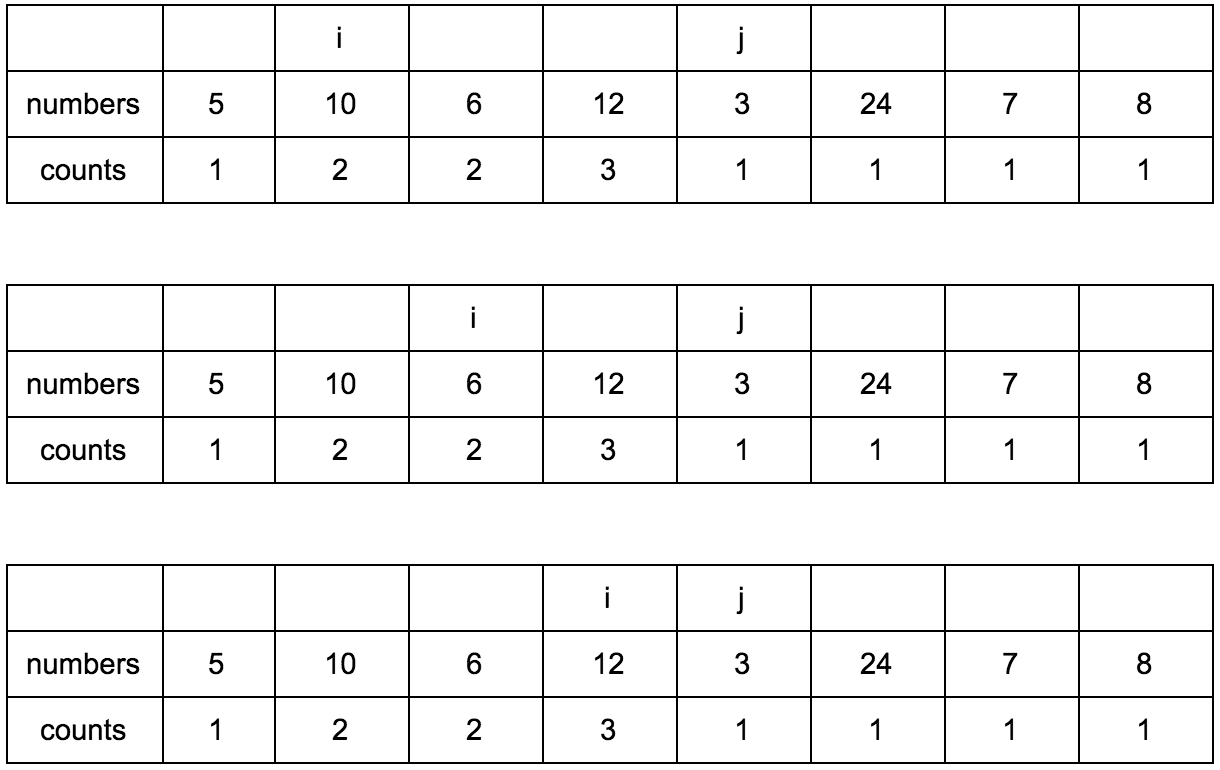
Shift j.

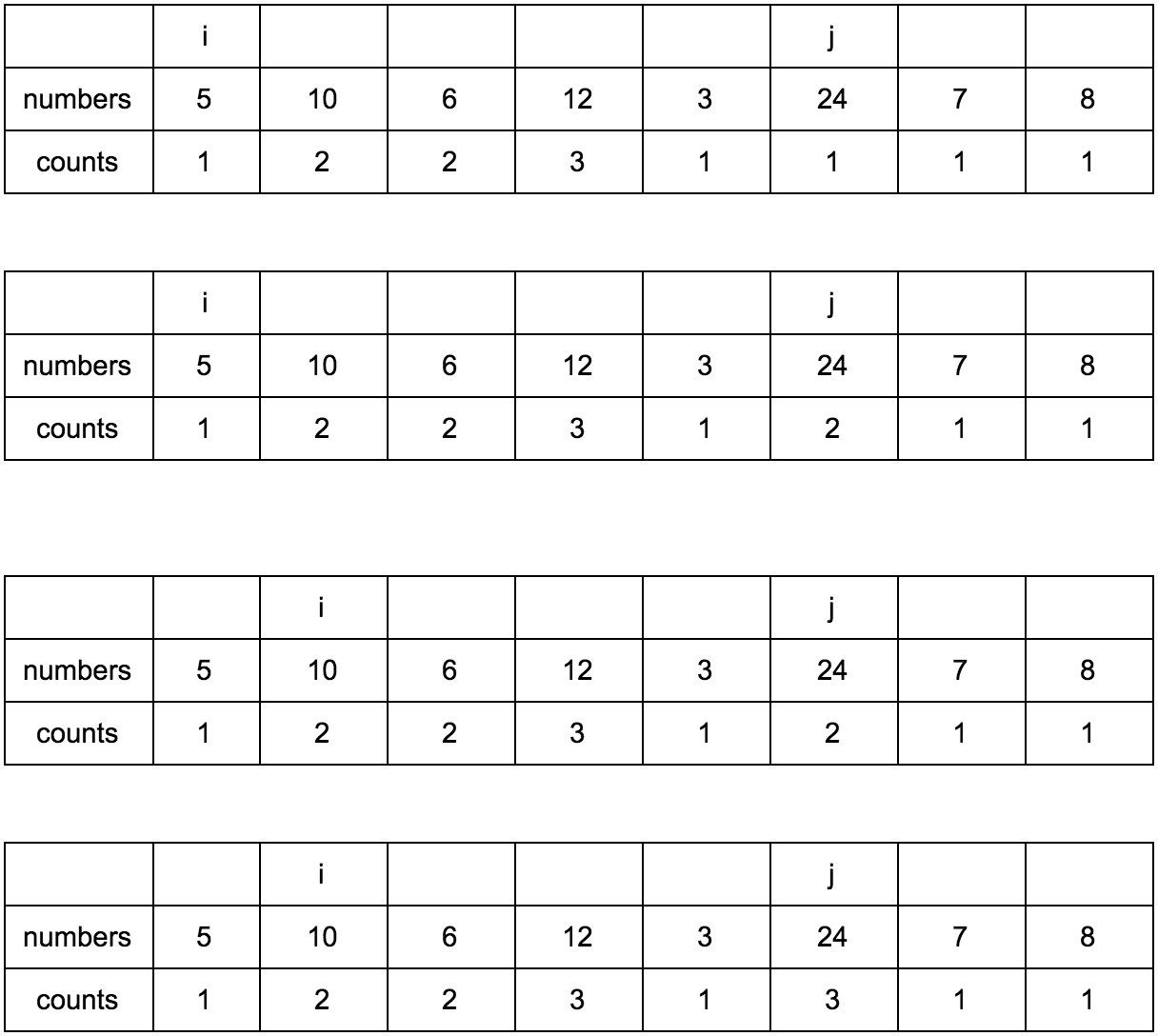
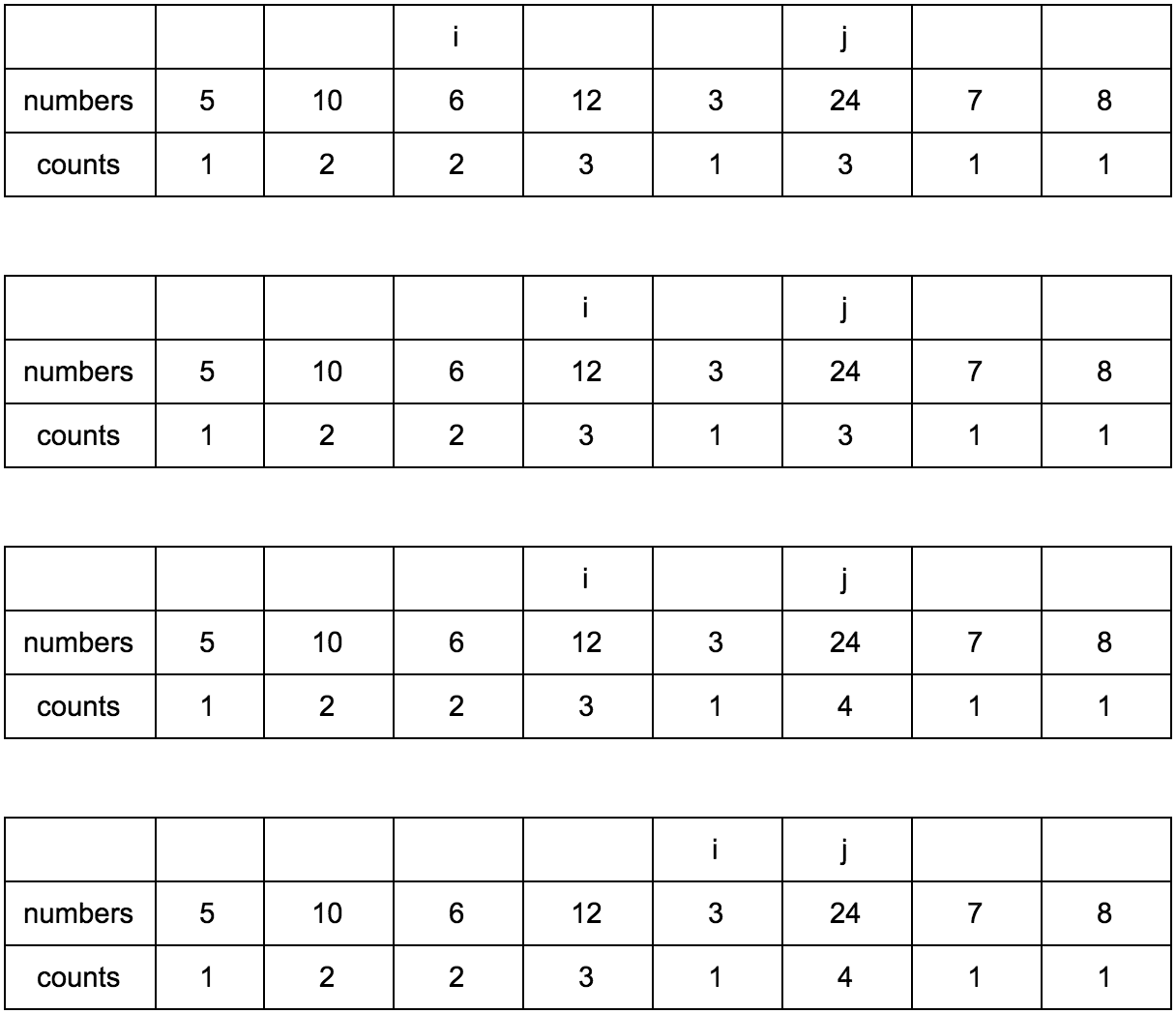
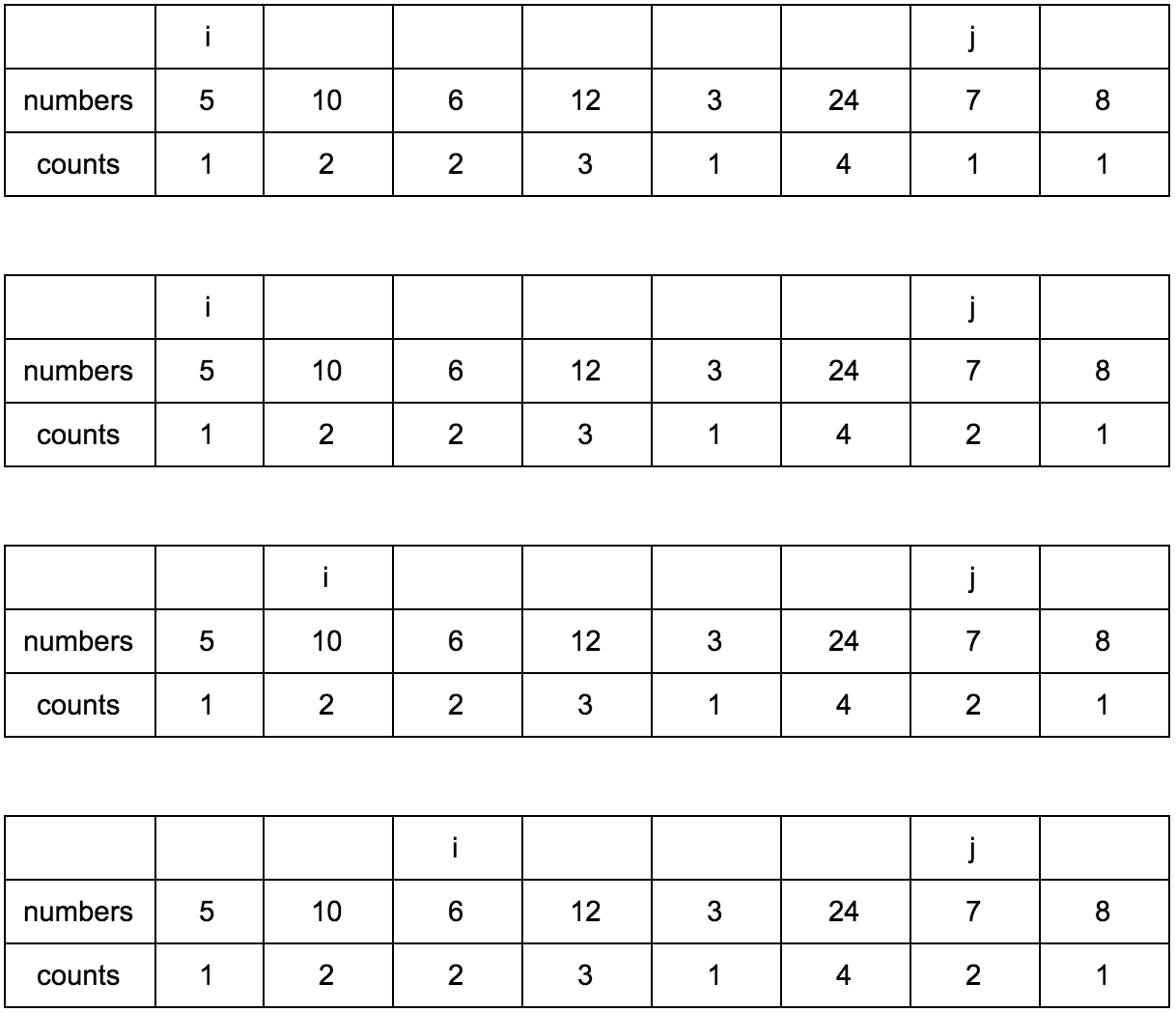
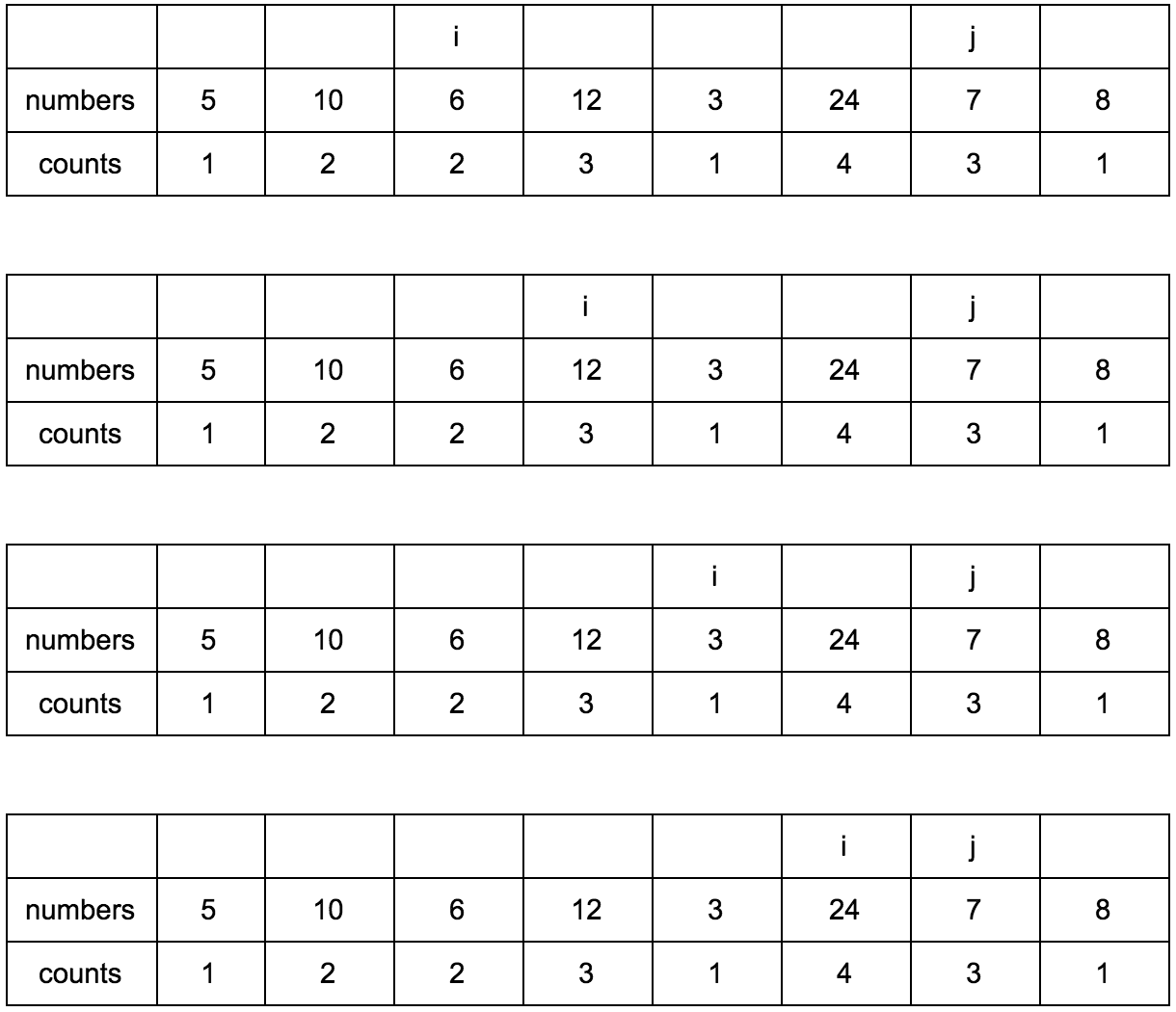
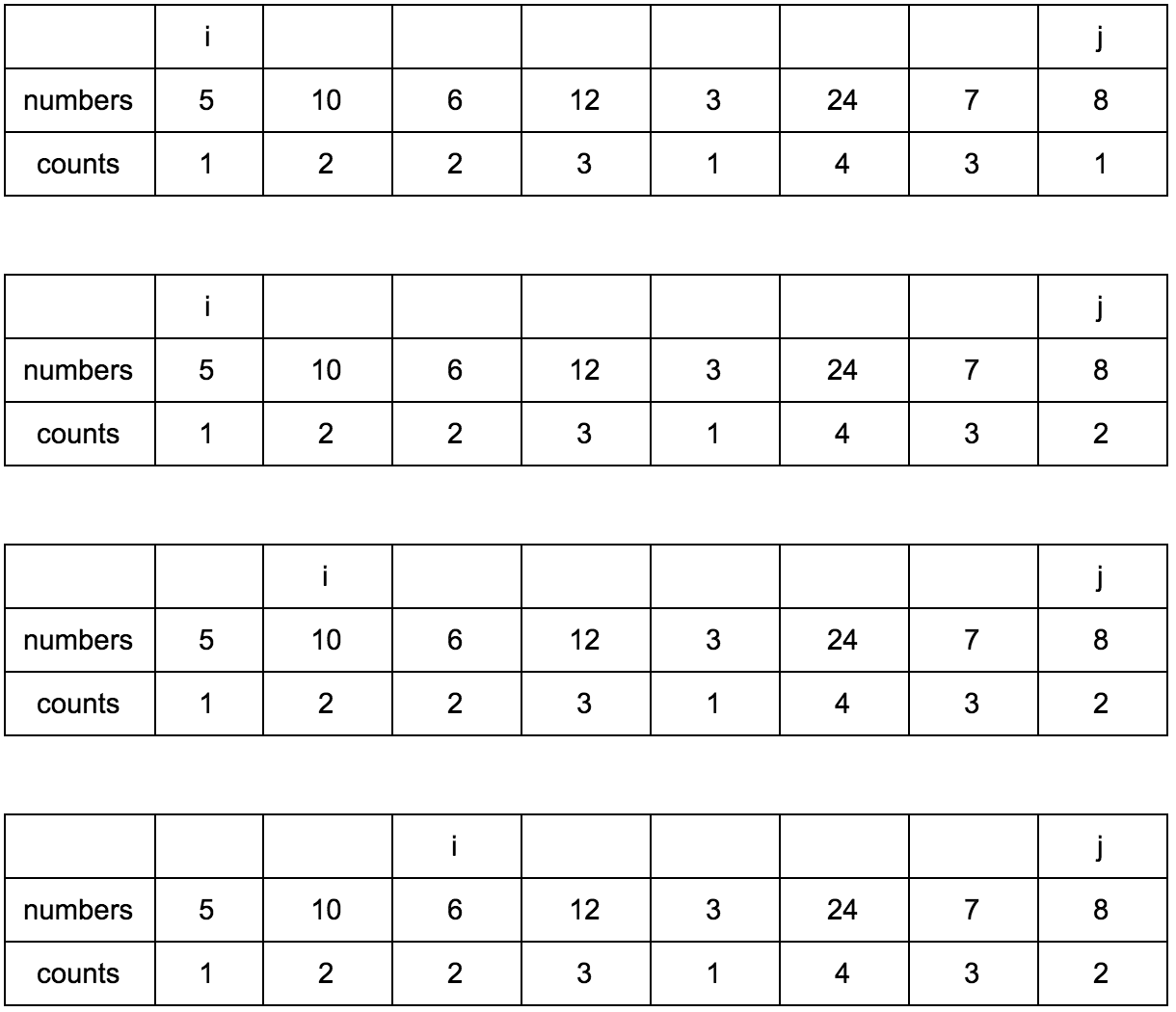
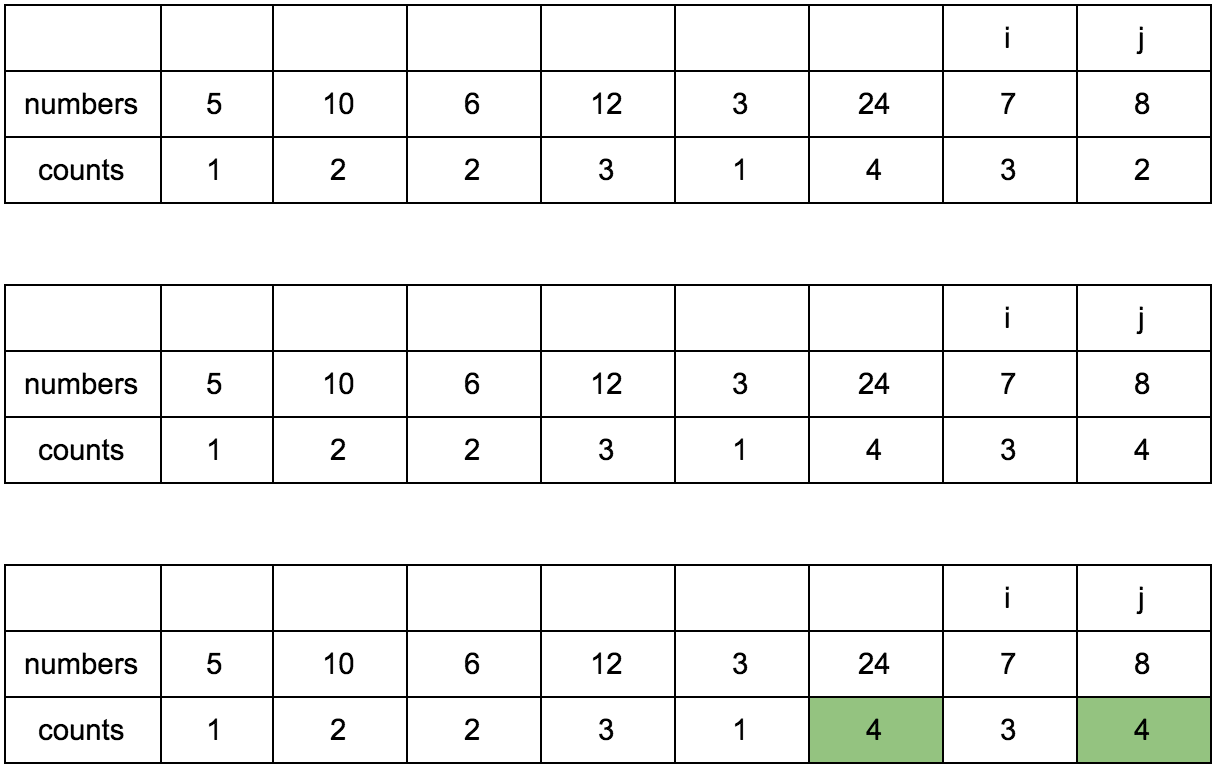
Result:

Having this table in front of our eyes and understanding what steps need to be taken, we can now easily implement it in code.

 int longestIncreasingSubsequenceLength( int numbers[] ) { if (numbers.count == 1) { return 1; } int lengthOfSubsequence[] = rray.newArrayOfSize(numbers.count, 1); for (int j = 1; j < numbers.count; j++) { for (int k = 0; k < j; k++) { if (numbers[j] > numbers[k]) { if (lengthOfSubsequence[j] <= lengthOfSubsequence[k]) { lengthOfSubsequence[j] = lengthOfSubsequence[k] + 1; } } } } int maximum = 0; for (int length in lengthOfSubsequence) { maximum = MAX(maximum, length); } return maximum; } 

→ Implementation on Objective-C
→ Tests

You could not help noticing the two nested loops in the code, and where there are two nested loops running through the same array, there is also a quadratic complexity O (n ^ 2), which is usually not good.

Now, if you are a bilingual , you will undoubtedly ask yourself “Can we do better?”, But ordinary mortals will ask, “Can I think of an algorithm that can do this in less time?”

The answer is “yes you can!”

To do this, we need to remember what binary search is.

Binary search O (log n)

Binary search works only on sorted arrays. For example, we need to find the position of the number n in a sorted array:
1, 5, 6, 8, 14, 15, 17, 20, 22

Knowing that the array is sorted, we can always say to the right or left of a certain number in the array the required number should be.

We are looking for the position of the number 8 in this array. Which side of the middle of the array it will be? 14 is the number in the middle of the array. 8 <14 - therefore 8 to the left 14. Now we are no longer interested in the right part of the array, and we can drop it and repeat the same operation again and again until we stumble on 8. As you see, we don’t even need to go through all the elements of the array , the complexity of this algorithm is <O (n) and is equal to O (log n).

To implement the algorithm, we need 3 variables for the indices: left, middle, right.

Looking for the position of the number 8.

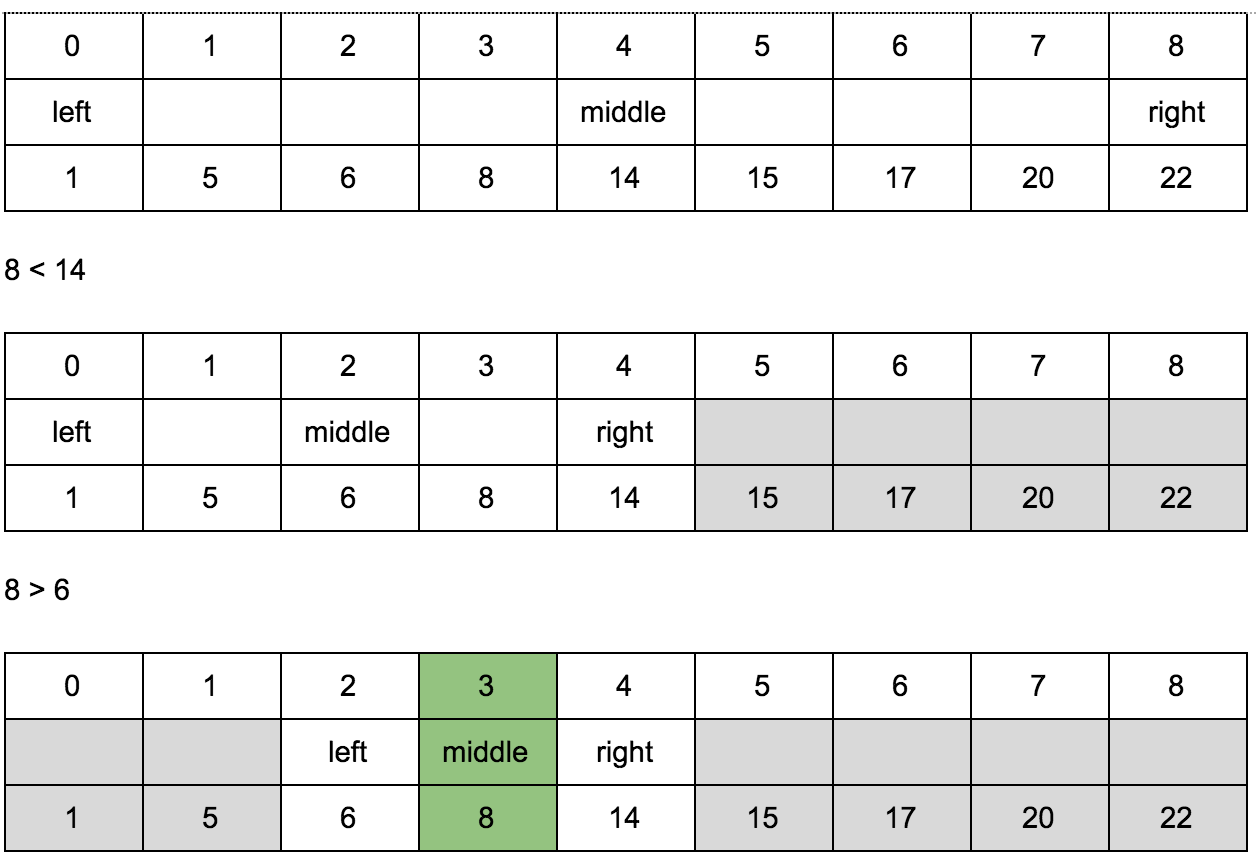
We guessed where is 8 from three notes.

 int binarySearch(int list [], int value) { if !list.isEmpty { int left = list.startIndex int right = list.endIndex-1 while left <= right { let middle = left + (right - left)/2 if list[middle] == value{ return middle } if value < list[middle]{ right = middle - 1 } else{ left = middle + 1 } } } return nil } 

Solution for O (n * log n)

Now we will go through our original array while filling in a new array in which the growing subsequence will be stored. Another plus of this algorithm: it finds not only the length of the maximum increasing subsequence, but also the subsequence itself.

How does binary search help us in filling in an array of subsequences?

With the help of this algorithm, we will look for a place for a new element in the auxiliary array, in which we store for each subsequence length the minimum element on which it can end.

If the element is greater than the maximum element in the array, add the element to the end. It's simple.

If such an element already exists in the array, nothing much changes. It's easy too.

What we need to consider is the case when the next element is less than the maximum in this array. It is clear that we cannot put it to the end, and it does not necessarily have to be a member of the maximal sequence at all, or vice versa, the subsequence that we have now and which this new element does not belong to may not be maximal.

All this is confusing, now it will be easier, we will reduce to the consideration of the 2 remaining cases.

1. The considered element of the sequence (x) is smaller than the largest element in the array (Nmax), but larger than the last one.
2. The considered element is less than some element in the middle of the array.

In case 1, we can simply fold Nmax in the array and put x in its place. Since it is clear that if the subsequent elements would be greater than Nmax, then they will be greater than x - accordingly, we will not lose a single element.

Case 2: in order for this case to be useful to us, we will create another array in which we will store the size of the subsequence in which this element is maximal. Actually this size will be the position in the first auxiliary array for this element, which we will find using a binary search. When we find the desired position, we check the element to the right of it and replace it with the current one if the current one is smaller (the same logic applies as in the first case)

Do not be discouraged if not everything has become clear from this textual explanation, now I will show everything clearly.

We need:

1. Source sequence
2. Create a mutable array where we will store the increasing elements for the subsequence.
3. Create a mutable array of sizes of a subsequence in which the element in question is the maximum.

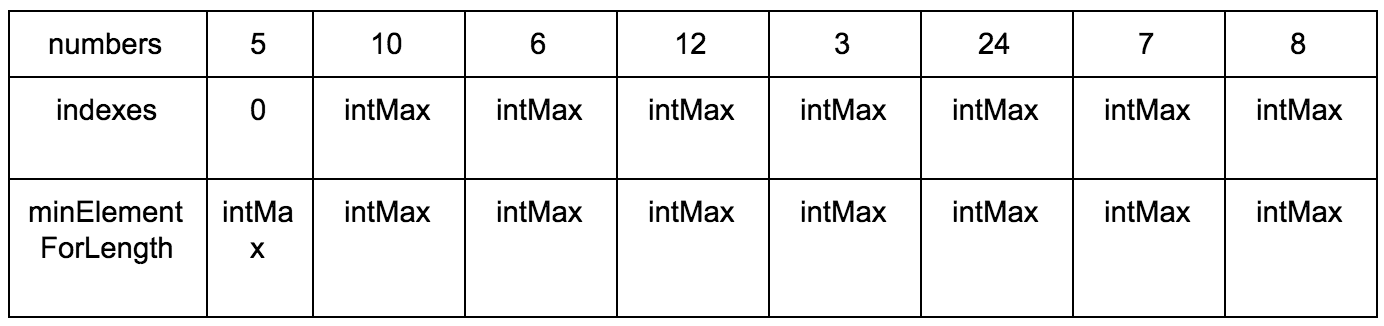
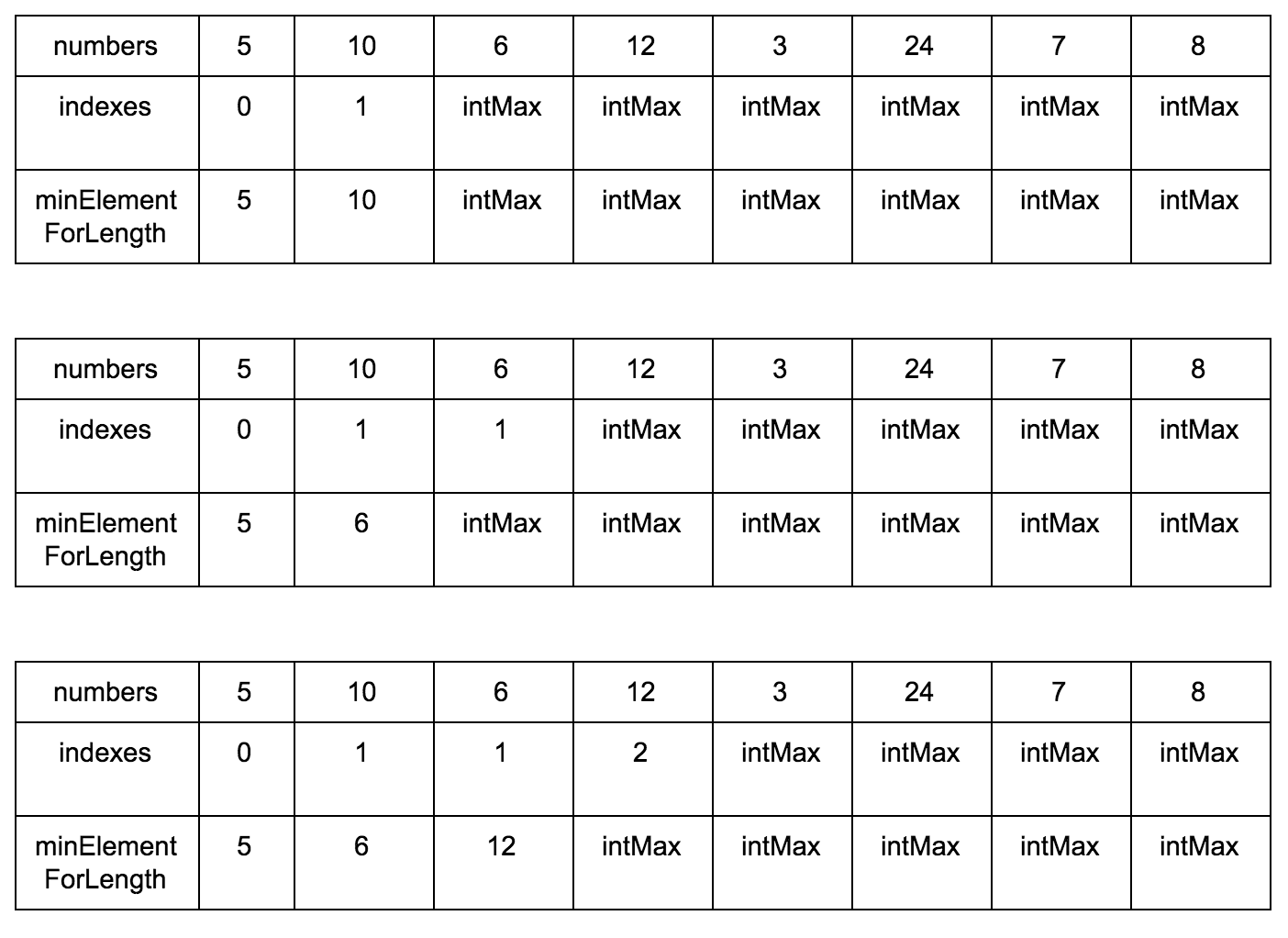
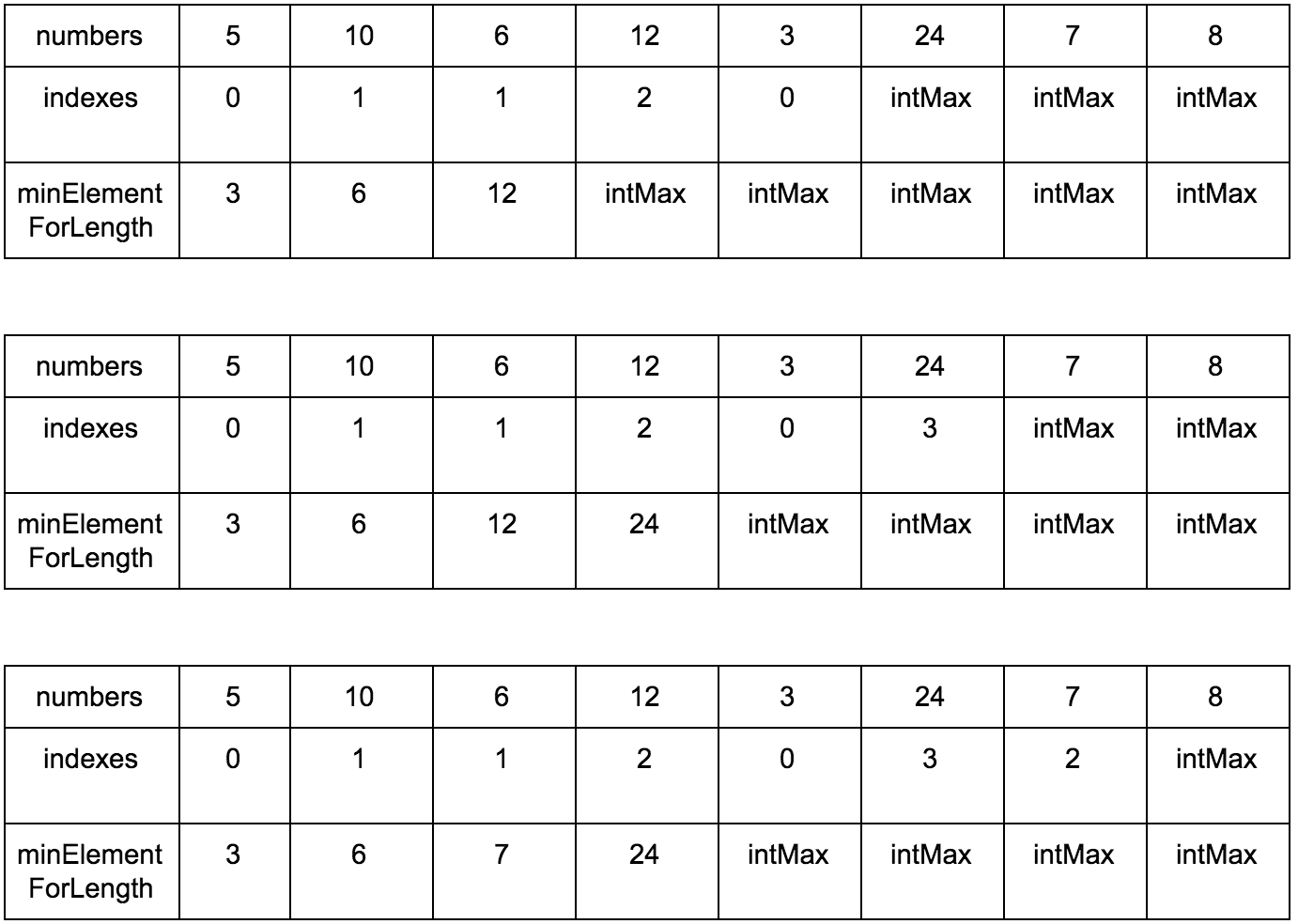
Result:

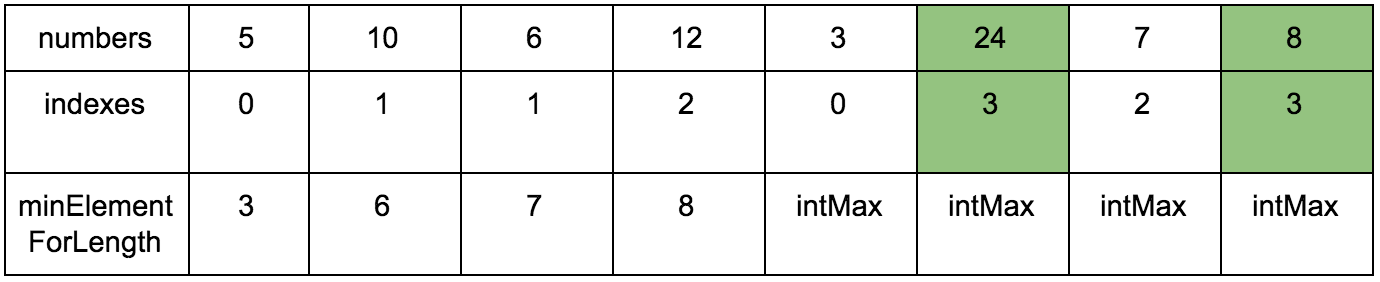
 int longestIncreasingSubsequenceLength(int numbers[]) { if (numbers.count <= 1) { return 1; } int lis_length = -1; int subsequence[]; int indexes[]; for (int i = 0; i < numbers.count; ++i) { subsequence[i] = INT_MAX; subsequence[i] = INT_MAX; } subsequence[0] = numbers[0]; indexes[0] = 0; for (int i = 1; i < numbers.count; ++i) { indexes[i] = ceilIndex(subsequence, 0, i, numbers[i]); if (lis_length < indexes[i]) { lis_length = indexes[i]; } } return lis_length + 1; } int ceilIndex(int subsequence[], int startLeft, int startRight, int key){ int mid = 0; int left = startLeft; int right = startRight; int ceilIndex = 0; bool ceilIndexFound = false; for (mid = (left + right) / 2; left <= right && !ceilIndexFound; mid = (left + right) / 2) { if (subsequence[mid] > key) { right = mid - 1; } else if (subsequence[mid] == key) { ceilIndex = mid; ceilIndexFound = true; } else if (mid + 1 <= right && subsequence[mid + 1] >= key) { subsequence[mid + 1] = key; ceilIndex = mid + 1; ceilIndexFound = true; } else { left = mid + 1; } } if (!ceilIndexFound) { if (mid == left) { subsequence[mid] = key; ceilIndex = mid; } else { subsequence[mid + 1] = key; ceilIndex = mid + 1; } } return ceilIndex; } 

→ Implementation on Objective-C
→ Tests

Results

We have now considered 4 algorithms of varying complexity. These are the difficulties that you have to constantly face when analyzing algorithms:

O (log n), O (n), O (n * log n), O (n ^ 2)

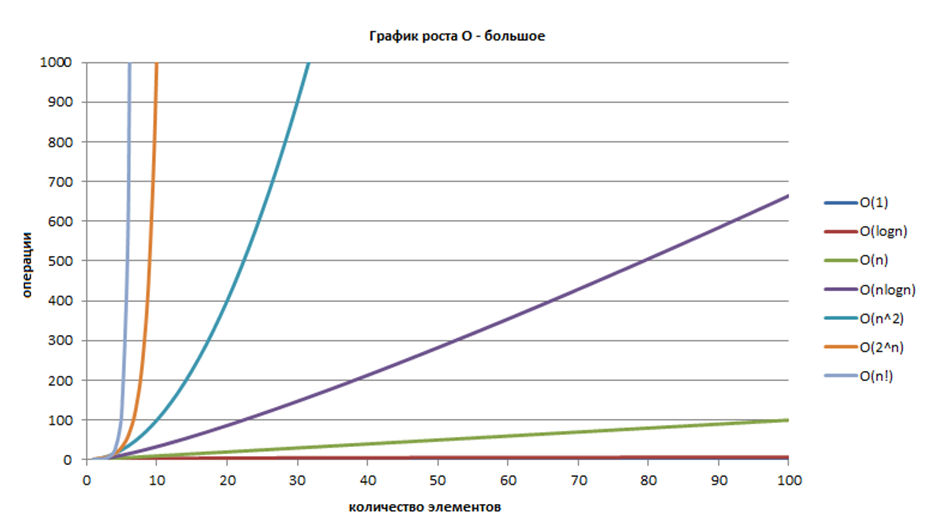
This picture from here this article

We also reviewed examples of the use of Dynamic Programming, thereby expanding our tool for developing and understanding algorithms. These principles will be useful to you in the study of other problems.

For better understanding, I recommend that you code these problems in your own language. And it would be great if you posted a link to your decision in the comments.

I also propose to think about how to modify the last algorithm in O (n * log n) so as to derive also the greatest subsequence itself. Answer write in the comments.

Thank you all for your attention, until we meet again!

References:
Question on Stackoverflow.com
Implementation examples in C ++ and Java
Video with explanation