Draw thick lines in WebGL

Ready examples

The examples are based on the OpenGlobus engine, which in this case is used as a wrapper over pure Javascript WebGL.

- Example for 2D case
- Example for the 3D case (use the W, S, A, D, Q, E keys and the cursor to move)

Introduction

In the process of working on the map library, I needed a tool to draw lines of different thickness. Of course, WebGL has a line drawing mechanism, but unfortunately you cannot set the line thickness. Therefore, the lines have to draw polygons, it is better to say triangles. On the Internet you can find several excellent articles, how to “triangulate” the line, what difficulties arise and how to solve them. Unfortunately, I did not find such an article from which I could copy the code and use it in my shader.
')
After many hours spent with a pencil and paper drawing an algorithm, and then many hours of debugging a completely not complicated glsl shader, I finally arrived at a result that could be achieved much faster. Hopefully, the WebGL polygonal line rendering approach described below will save the time of your life, which otherwise would be spent on the implementation of this task!

Drawing a line in two-dimensional space

In my shader engine for drawing lines in two-dimensional and three-dimensional spaces, almost the same code is used. The only difference is that for the three-dimensional case the projection of the three-dimensional coordinates of the line onto the screen is added, then the same algorithm.

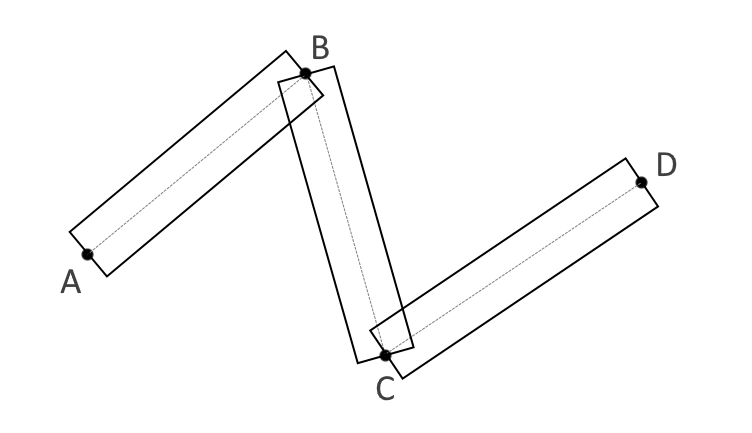
There is a common practice to make lines thick - to represent each line segment as a rectangle. The simplest representation of the thick line looks like this (Fig. 1) :

(fig. 1)

To get rid of visible segmentation at the nodal points, it is necessary to combine adjacent points of the neighboring segments, so as to maintain the thickness on both parts of the adjacent segments. To do this, find the intersection of one-sided faces of the line, above and below (Fig. 2) :


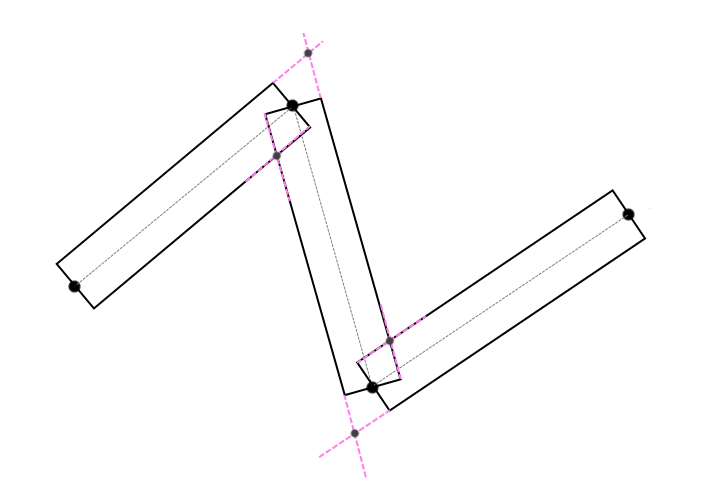
(fig. 2)

However, the angle between adjacent segments can be so sharp that the intersection point can go far from the junction point of these lines (Fig. 3) .


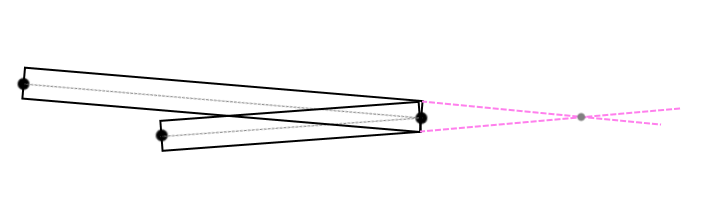
(pic. 3)

In this case, this angle must somehow be processed (Fig. 4) :


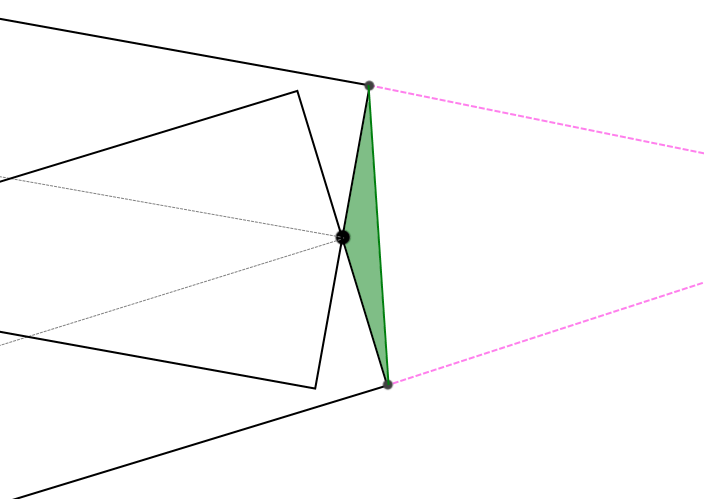
(pic. 4)

I decided to fill such areas with the corresponding triangles. The GL_LINE_STRING sequence came to my rescue, which, with the correct order, should, if the angle is too acute (the threshold value is checked in the vertex shader), create the effect of a neatly trimmed angle (Fig. 5) , or combine adjacent coordinates of adjacent segments according to the rule of intersection of one-sided faces (Figure 2) , as before.


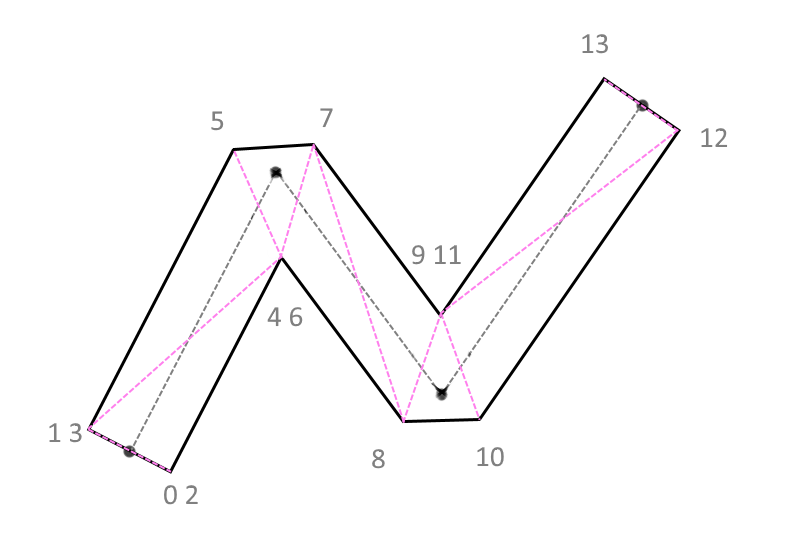
(pic. 5)

The numbers near the vertices are the indices of the vertices by which polygons are drawn in the graphics pipeline. If the angle is obtuse, in this case the triangle for cutting will merge into an infinitely thin line and become invisible (Fig. 6) .

(pic. 6)


We imagine the sequence in this way (Fig. 7) :


(fig. 7)

That's the whole secret. Now let's see how to render it. It is necessary to create a vertex buffer, an index buffer and an order buffer, which shows in which direction to thicken from the current vertex of the segment, as well as which part of the segment is currently being processed by the vertex shader, initial or final. In order to find the intersection of faces, in addition to the coordinates of the current point, we also need to know the previous and next coordinates from it (Fig. 8) .


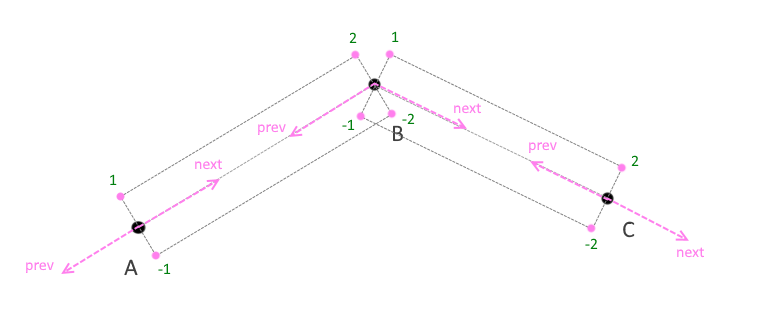
(pic. 8)

So, for each coordinate in the shader, we should have, in fact, the coordinate itself, the previous and next coordinates, the order of the point, i.e. whether the point is the beginning, or the end of a segment (I denote -1, 1 is the beginning and -2, 2 is the end of the segment) , how should it be located: above or below the current coordinate, as well as thickness and color.

Since WebGL allows you to use one buffer for different attributes, in the case that the element of this buffer is a coordinate, when you call vertexAttribPointer, each attribute is assigned in bytes the size of the buffer element, and the offset relative to the current attribute element. This is clearly seen if you draw a sequence on paper (fig. 9) :


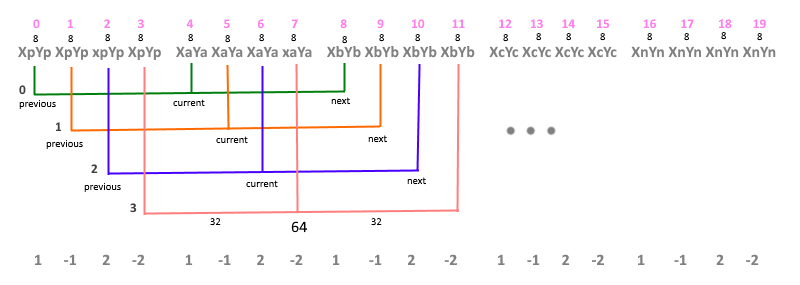
(pic 9)

The top line is the indices in the array of vertices; 8 - element size ( coordinate type vec2) i.e. 2x4 bytes; Xi, Yi - coordinate values ​​at points A, B, C ; Xp = Xa - Xb, Yp = Ya - Yb, Xn = Xc - Xb, Yn = Xc - Xb vertices indicating the direction at the border points. The color arcs depict a bunch of coordinates (previous, current, and next) for each index in the vertex shader, where current is the current coordinate of the bunch, previous is the previous coordinate of the bunch, and next is the next coordinate of the bunch. A value of 32 bytes is an offset in the buffer in order to identify the current (current) relative to the previous (previous) coordinate values, 64 bytes is an offset in the buffer to identify the next (next) value. Since Since the index of the next coordinate begins with the previous (previous) value, then for it the offset in the array is zero. The last line shows the order of each coordinate in the segment, 1 and -1 is the beginning of the segment, 2 and -2 respectively, the end of the segment.

In code, it looks like this:

var vb = this._verticesBuffer; gl.bindBuffer(gl.ARRAY_BUFFER, vb); gl.vertexAttribPointer(sha.prev._pName, vb.itemSize, gl.FLOAT, false, 8, 0); gl.vertexAttribPointer(sha.current._pName, vb.itemSize, gl.FLOAT, false, 8, 32); gl.vertexAttribPointer(sha.next._pName, vb.itemSize, gl.FLOAT, false, 8, 64);  gl.bindBuffer(gl.ARRAY_BUFFER, this._ordersBuffer); gl.vertexAttribPointer(sha.order._pName, this._ordersBuffer.itemSize, gl.FLOAT, false, 4, 0); 

This is a function that creates arrays of vertices and orders, where pathArr is an array of coordinate arrays for which arrays are filled to initialize buffers, outVertices is an array of coordinates, outOrders is an array of orders and outIndexes is an array of indices:

 Polyline2d.createLineData = function (pathArr, outVertices, outOrders, outIndexes) { var index = 0;  outIndexes.push(0, 0);  for ( var j = 0; j < pathArr.length; j++ ) {   path = pathArr[j];      var startIndex = index;      var last = [path[0][0] + path[0][0] - path[1][0], path[0][1] + path[0][1] - path[1][1]];      outVertices.push(last[0], last[1], last[0], last[1], last[0], last[1], last[0], last[1]);      outOrders.push(1, -1, 2, -2); //     4       for ( var i = 0; i < path.length; i++ ) {       var cur = path[i];          outVertices.push(cur[0], cur[1], cur[0], cur[1], cur[0], cur[1], cur[0], cur[1]);          outOrders.push(1, -1, 2, -2);          outIndexes.push(index++, index++, index++, index++);      }      var first = [path[path.length - 1][0] + path[path.length - 1][0] - path[path.length - 2][0], path[path.length - 1][1] + path[path.length - 1][1] - path[path.length - 2][1]];      outVertices.push(first[0], first[1], first[0], first[1], first[0], first[1], first[0], first[1]);      outOrders.push(1, -1, 2, -2);      outIndexes.push(index - 1, index - 1, index - 1, index - 1);      if ( j < pathArr.length - 1 ) {      index += 8;          outIndexes.push(index, index);      }  } }; 

Example:

 var path = [[[-100, -50], [1, 2], [200, 15]]]; var vertices = [],  orders = [],  indexes = []; Polyline2d.createLineData(path, vertices, orders, indexes); 

We get:

vertices: [-201, -102, -201, -102, -201, -102, -201, -102, -100, -50, -100, -50, -100, -50, -100, -50 , 1, 2, 1, 2, 1, 2, 1, 2, 200, 15, 200, 15, 200, 15, 200, 15, 399, 28, 399, 28, 399, 28, 399, 28]

orders: [1, -1, 2, -2, 1, -1, 2, -2, 1, -1, 2, -2, 1, -1, 2, -2, 1, -1, 2, -2]

indexes: [0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 11, 11, 11, 11]

Vertex shader:

 attribute vec2 prev; //  attribute vec2 current; //  attribute vec2 next; //  attribute float order; //             uniform float thickness; // uniform vec2 viewport; //  //    vec2 proj(vec2 coordinates){ return coordinates / viewport; }             void main() { vec2 _next = next;   vec2 _prev = prev; //   ,       if( prev == current ) {   if( next == current ){       _next = current + vec2(1.0, 0.0);           _prev = current - next;       } else {       _prev = current + normalize(current - next);       }  }   if( next == current ) {    _next = current + normalize(current - _prev);   }                    vec2 sNext = _next,           sCurrent = current,           sPrev = _prev; //   ,        vec2 dirNext = normalize(sNext - sCurrent);   vec2 dirPrev = normalize(sPrev - sCurrent);   float dotNP = dot(dirNext, dirPrev);  //     vec2 normalNext = normalize(vec2(-dirNext.y, dirNext.x));   vec2 normalPrev = normalize(vec2(dirPrev.y, -dirPrev.x));   float d = thickness * 0.5 * sign(order);                    vec2 m; //m -  ,           if( dotNP >= 0.99991 ) {   m = sCurrent - normalPrev * d;   } else {   vec2 dir = normalPrev + normalNext; //        (. 2)       m = sCurrent + dir * d / (dirNext.x * dir.y - dirNext.y * dir.x);      //            if( dotNP > 0.5 && dot(dirNext + dirPrev, m - sCurrent) < 0.0 ) {       float occw = order * sign(dirNext.x * dirPrev.y - dirNext.y * dirPrev.x); //      LINE_STRING           if( occw == -1.0 ) {           m = sCurrent + normalPrev * d;           } else if ( occw == 1.0 ) {           m = sCurrent + normalNext * d;           } else if ( occw == -2.0 ) {           m = sCurrent + normalNext * d;           } else if ( occw == 2.0 ) {           m = sCurrent + normalPrev * d;          } // ""  ,              } else if ( distance(sCurrent, m) > min(distance(sCurrent, sNext), distance(sCurrent, sPrev)) ) {      m = sCurrent + normalNext * d;       }  }   m = proj(m);   gl_Position = vec4(mx, my, 0.0, 1.0); } 

A few words in conclusion

This approach is implemented for drawing tracks, orbits , vector data .

In conclusion, I want to add a few ideas on what can be done with the algorithm in order to improve the quality of the lines. For example, you can pass a color in the colors attribute for each vertex, then the line will become multicolored. Also, each vertex can transmit width, then the line will vary in width from point to point, and if we calculate the width at a point (in the vertex shader) relative to the distance from the observation point (for the three-dimensional case) , the effect can be achieved when the part of the line located closer to the point of observation is visually larger than the part of the line that is at a distance. You can also implement anti-aliasing (antialiasing) by adding two passes for each of the edges of the thick line, in which thin lines are drawn (a frame around the edges) with little transparency relative to the central part.