Fuzzy search by name
Good day. The problem with the search, service or product occurs on the vast majority of sites. And for the most part, the realization of such an opportunity is limited to searching for the exact word that was entered in the search box.
If there is time, and the customer wants a little more, then the Google implementation of the most popular algorithm (which is the “Levenshtein distance”) and enter it.
In this article, I will describe a strongly modified algorithm based, however, at Levenshtein distances, and give examples of C # code for a fuzzy search by name, for example: cafes, restaurants, or certain services ... In general, everything that can be listed and has from one to several words in its composition:
')
Yandex, Mail, ProjectArmata, world of tanks, world of warships, world of warplanes, etc.
For those unfamiliar with the algorithm, I recommend reading first the articles " Implementing a Fuzzy Search ," " Fuzzy Search in the Text and the Dictionary, " or its description in my presentation under the slider.
And it would seem - this is it! Everything is invented for us and there is nothing to do at all, but there is a problem ...
1) Taking weight coefficient 1 is always not quite right, because the probability of a typo depends on several specific factors: the distance of the keys on the keyboard, phonetic groups, and even the banal speed of typing.
2) The idea of Levenshtein is designed to “find differences between words,” rather than part of words, which is critical for dynamic output as letters are entered.
3) The names of the services have in their structure more than one word, then the person may simply not remember in what order they go.
We also take into account several factors, such as:
• keyboard layout in another language
• transliteration of characters
We will try to solve these problems in this article.
To begin with, let's agree that all the words we will lead to one single register. In my version of the code, I chose lower case, this will be reflected in the references that we need (these references will be given in the course of the description). In the article itself, I will resort to different writing styles, for example, “CamelCase” - ProjectArmata, but this is done solely for the convenience of human perception, from the point of view of analysis, the register is one (lower). And yet, we will take as a basis not the classical, but the optimized version of the code for finding the Levenshtein distance from here :
Adjust it a little by removing the reordering of words. For Levenshtein's algorithm, word order does not matter, but for us it will be important for other reasons. As a result, we got the following:
Let's start improving the search algorithm with changes in weighting factors. First we make the insertion and deletion coefficients equal to 2.
Those. the lines will change:
And here is the line for calculating the replacement rate of characters, we, turning into a function CostDistanceSymbol:
And we will consider two factors:
1) Keyboard distance
2) Phonetic groups
In this regard, for more convenient work with source and target objects, we will turn them into an object:
To do this, you will need the following auxiliary directories:
The ratio of key codes of the Russian keyboard:
The ratio of key codes for the English keyboard
Thanks to these two reference books, mathematically speaking, we can transform two different character spaces into one single universal.
And the following relations will be fair there:
private static SortedDictionary <int, List> DistanceCodeKey = new SortedDictionary <int,
Those. we take the keys standing around the other key. You can verify this by the example of the figure:
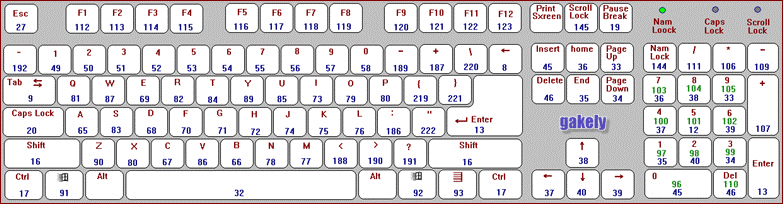
Yes, I know that in addition to the QWERTY keyboard, there are other layouts, and then the table of keyboard distances will not match, but we take the most common option.
If someone knows a better way - please write.
Now we are ready for the first stage - calculating the weight of the error symbol in the CostDistanceSymbol function:
As it was before, if the characters are the same, then the distance is 0:
If the key codes are the same, then the distance is also 0:
If you have a question why we compare key codes after comparing characters, the answer is simple - we want the words “Water” and “Djlf” to be perceived the same way. And the characters that can be typed on different layouts, for example, ";" or "," regardless of the layout, were also perceived the same way.
Further, we are only looking at the codes how closely the key codes are from each other. If close, then distance 1, and if not, then 2 (exactly the same weight as when inserting or deleting):
In fact, such a small refinement covers a huge number of random errors ranging from the wrong layout, ending with a miss by the key.
But after the typing errors, a person simply may not know how words are spelled. For example: pike, posh. test
Such words are not only in Russian, but also in English. Similar cases we also need to take into account. For the English words, we take as a basis the work of Zobel and Dart on phonetic groups .
"Aeiouy", "bp", "ckq", "dt", "lr", "mn", "gj", "fpv", "sxz", "csz"
And for Russian, I will compile myself on a whim:
“Yiy”, “ee”, “aya”, “oee”, “yu”, “sc”, “oa”, “yo”
These phonetic groups are converted into an object of the type:
This can be done by hand or as I write code, but the result will be the same. And now after checking the key code, you can check the letters for entering the phonetic group with the same logic of finding errors as in the previous step:
In addition to the above missed typos, there are typos "typing speed" of the text. This is when two consecutive letters people, when typing, confused places. Moreover, this is such a common mistake that a certain mathematician Frederick Damerau modified the Levenshtein algorithm by adding a transposition (permutation) of characters.
From a programmatic point of view, we add the following to the LevenshteinDistance function:

Thus, we have completed the first paragraph to refine the code. Go to the second paragraph. Recall that the Levenshtein idea is intended to “find differences between words,” and not part of the words, which is critical for dynamic output results as letters are entered.
For example, in the directory there are two words:
• “ProjectArmata”
• "Yak"
Entering the query “Pro” in the search bar, we get “Yak” as a higher priority, due to the fact that replacing two characters and deleting one will be only 3 parrots (taking into account unit coefficients and the classical Levenshtein algorithm, without our modifications), Adding part of the word "jectArmata" 10 parrots.
The most logical in this situation is not to compare the whole word, but only a part of the desired word with the entered string.
Since the search query consists of three characters “Pro”, we will take the first three characters from the word “ProjectArmata”, i.e. “Pro” and get 100% match. For this particular case - perfect. But let's consider some more options. Suppose we have in the database, there is the following set of words:
• "Communal"
• "Conveyor"
• "The colony"
• “Cosmetics”
The search query will look like “com”. As a result, words will have the following match factors:
Communal - 0
Conveyor - 1
Colony - 1
Cosmetics - 1
If everything is normal with the word “Kommunalka”, then the other three words look somehow uniform ... Although it is clear that, perhaps, the person described himself in one letter and he is looking for “Cosmetics”, and not Conveyor or Colony. And our task is to give him the most suitable result, and not just everything. Especially, as Damerau said - most of the errors are transpositions of letters.
To eliminate such a mistake, we do a little refinement:
Take not the first “n” letters, but “n + 1” letters, where n is the number of letters in the query. And then the coefficients when querying "Com" will be as follows:
Communal - 1
Cosmetics - 1
Conveyor - 2
Colony - 2
“Cosmetics” was corrected, but “Kommunalka” left ... But I like this option more for what reasons. Usually, if a search is required, initially the information is shown to the user in the form of a drop-down list, under the search line, as letters are entered. The length of this drop-down list is limited in size to 3-7 entries. As a consequence, if there are only three entries, then in the second version they will appear: “Communal”, “Cosmetics” and “Conveyor” [as he is stupid first in issuing because of a guid, or simply because of the date of creation]. And in the first case there will be “Communal”, “Conveyor”, “Colony” and no “Cosmetics”, since she was not lucky for other reasons ...
Of course, this problem has other solutions. For example, sort first, by “n” letters, and then, take those groups of words from whom the indices coincided and additionally re-sort the “n + 1” letters and you can again, and again ... Here it is solved individually depending on the data in the database , solvable problem, computing power.
Let's not now focus on solving the above problem ... We are only in the middle of the road and I still have something to tell.
The following nuance in the correct search results comes to us from the times of the USSR. Then they loved to make names consisting of several words combined into one. And now it is relevant:
Consumer union
GazPromBank
Agricultural Bank
ProjectArmata
BankURALSIB
Etc.
[ps I know that some of the names are separated by spaces, but I needed to pick some vivid examples]
But, if we follow our algorithm, we always take the first "n + 1" letters from the word. And if a person picks up the word "Bank", he will not receive an adequate issuance. Since we will compare the lines:
"Bank"
"Potre"
"Gazpr"
Rosse
"Proje"
To find the word "bank" regardless of position, we will need to make a floating window for the phrase and return the smallest coefficient:
As you can see, to the error obtained after calculating the Levenshtein distance, we add another value (i * 2 / 10.0). If with “i * 2” everything is clear, this is a mistake of inserting letters at the beginning of a word, like the classical algorithm for finding the Levenshtein distance, but why do we divide it by 10? The bottom line is that if we just leave “i * 2”, then words that are stupidly shorter in length will fall into the issue of claim and we will again get away from the name of the banks. And so the coefficient has to be divided by 10, which is to reduce this offset. Why exactly 10? For our base, it was more or less normal, but I do not exclude that it can be divided into more. Everything depends on the length of the words and how similar the words are. I will give the calculation of the most suitable coefficient a little later.
With words, as well as the search unit, sort of sorted out, now go to the phrases. And first, again, a few examples:
• warface
• world of tanks
• world of warplanes
• world of ships
Let's understand what we basically need from searching for a phrase. We need the missing words to be added, the extra phrases deleted, and also that they change places. Somewhere I have already said this ... And, exactly, I remembered ... At the beginning of the article, when I was talking about the words and the function of Levenshtein distance. In order not to waste your time, I will immediately say that it did not work out in its pure form, but inspired by her, she managed to write code applicable to phrases.
As with the implementation of the Levenshtein distance function, if one of the phrases is empty, then we return an error value equal to the insertion or deletion [depending on which side the empty phrase came from] of all the letters.
Those. we summarize the number of letters in the phrase multiplied by 2 (this coefficient was chosen at the beginning of the article for letters) and multiplied by 100. These 100 are the most controversial coefficient in the whole algorithm. For what it will be needed more clearly presented below, and then I will explain that, in theory, it must be calculated, and not just taken from the ceiling.
In this code, we match each word from the record in the database with each of the search query and take the smallest coefficients for each word. The total coefficient for the phrase is as follows:
result + = minRangeWord * 100 + (Math.Abs (i - minIndex) / 10.0);
As you can see, all the logic is the same as described earlier, the minimum coefficient for the word minRangeWord is multiplied by our 100 and summed up with the coefficient that shows how close the word is to its most suitable position (Math.Abs (i - minIndex) / 10.0).
A multiplication of 100 is used to compensate for the incremental coefficient that may occur when searching for the most suitable position of the search word in the previous step. As a result, this coefficient can be calculated as the largest between the phrase in the search line and all the words in the database. Not phrases, namely words. But for this, it would be necessary to measure the Levenshtein distance with our modifications to “empty” with our modifications, which is very wasteful in terms of resources.
Those. get rid of the function GetRangeWord and take the maximum value of the deviation of the phrase “i * 2” from the most appropriate place. And then take the highest value to bring it to the nearest larger tenfold number (10, 100, 1000, 10000, 100000, etc.). Thus we get two values:
The first is the value to which the mixed word should be divided in the GetRangeWord function. The second is the value that you need to multiply minRangeWord to compensate for the previous offset. In this way we will get accurate indicators of phrase similarity. But in practice one can neglect large deviations, and estimate the average approximately ... What I actually did.
In principle, everything. The main questions I have left out are just a slight refinement of the “transliteration of characters”. The difference between the above described search and the search in transliteration is that, in the CostDistanceSymbol function, we will not adjust the response values by key distance, since The issue in this case will not be correct.
It can also be noted that the adequate output of the result begins with 3 characters in the search string; if the symbol is smaller, it is better to use a more clumsy method with accurate string matching.
Next, I will give the most complete code of all the above described, but first:
1) This code was written by me personally in my free time.
2) The algorithm was thought out by me personally in my free time.
Separately, I want to say thank you for the links and inspiration: Dmitry Panyushkin, Pavel Grigorenko.
The names that are given in the article are taken from public sources and belong to their owners. Not an advertisement.
Thanks to everyone who read. Criticism and advice are welcome.
Vitaly Alferov, 2017
If there is time, and the customer wants a little more, then the Google implementation of the most popular algorithm (which is the “Levenshtein distance”) and enter it.
In this article, I will describe a strongly modified algorithm based, however, at Levenshtein distances, and give examples of C # code for a fuzzy search by name, for example: cafes, restaurants, or certain services ... In general, everything that can be listed and has from one to several words in its composition:
')
Yandex, Mail, ProjectArmata, world of tanks, world of warships, world of warplanes, etc.
For those unfamiliar with the algorithm, I recommend reading first the articles " Implementing a Fuzzy Search ," " Fuzzy Search in the Text and the Dictionary, " or its description in my presentation under the slider.
Levenshtein distance algorithm
Levenshtein distance is the most popular algorithm in the network for finding the degree of difference between two words. Namely, what is the minimum number of actions that must be performed to obtain the second from the first line.
There are only three such actions:
• Delete
• Insert
• Replacement
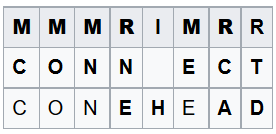
For example, for 2 lines "CONNECT" and "CONEHEAD" you can build the following conversion table:
In theory, transaction prices may depend on the type of operation (insert, delete, replace) and / or on the symbols involved in it. But in general:
w (a, ε) is the cost of deleting the character “a”, equals 1
w (ε, b) is the insertion price of the character “b”, equals 1
w (a, b) - the price of replacing the character “a” with the character “b” equals 1
Everywhere put units.
And from the point of view of mathematics, the calculation looks like this.
Let S1 and S2 be two lines (of length M and N respectively) over some alphabet, then the editorial distance (Levenshtein distance) d (S1, S2) can be calculated by the following recurrent formula:
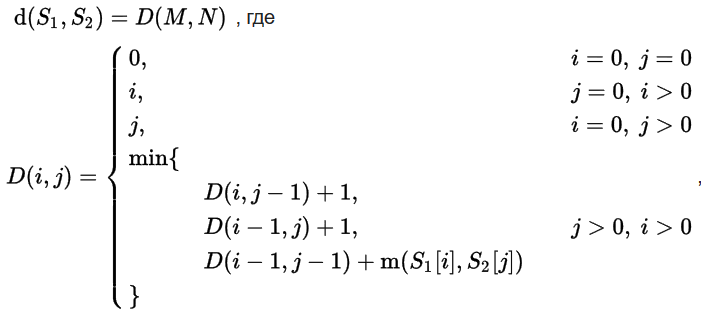
The "default implementation" of the Levenshtein algorithm was made by two mathematicians Vanger and Fisher [not to be confused with a chess player].
And it looks like in C # like this:
Taken from here .
And visually, the work of the algorithm for the words “Prisoner” and “Dagestan” is as follows:
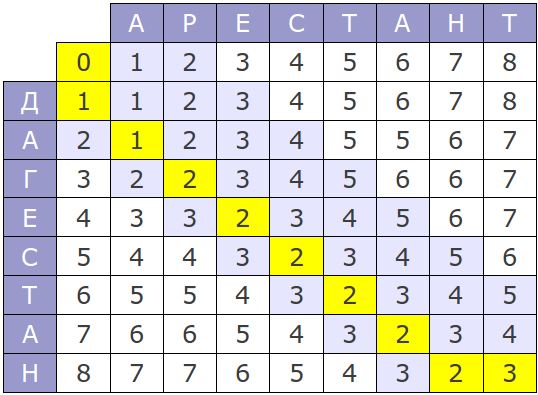
The extreme right-bottom corner of the matrix indicates how different the words are. From the matrix, that in this particular case, the difference between the words is 3 conditional parrots.
If it is not clear, then we will look at these words in another representation:
_ A R E S T A N T
D A G E S T A N
Thus, it turns out that in order to turn the word “Arrestant” and “Dagestan”, you need to add one letter “D”, replace one letter “P” with “G” and remove the letter “T”. Since All actions have a weight of 1, then the difference in words is 3 parrots.
If the words completely coincide, then the distance will be 0. That's the whole theory, everything ingenious is simple.
There are only three such actions:
• Delete
• Insert
• Replacement
For example, for 2 lines "CONNECT" and "CONEHEAD" you can build the following conversion table:

In theory, transaction prices may depend on the type of operation (insert, delete, replace) and / or on the symbols involved in it. But in general:
w (a, ε) is the cost of deleting the character “a”, equals 1
w (ε, b) is the insertion price of the character “b”, equals 1
w (a, b) - the price of replacing the character “a” with the character “b” equals 1
Everywhere put units.
And from the point of view of mathematics, the calculation looks like this.
Let S1 and S2 be two lines (of length M and N respectively) over some alphabet, then the editorial distance (Levenshtein distance) d (S1, S2) can be calculated by the following recurrent formula:
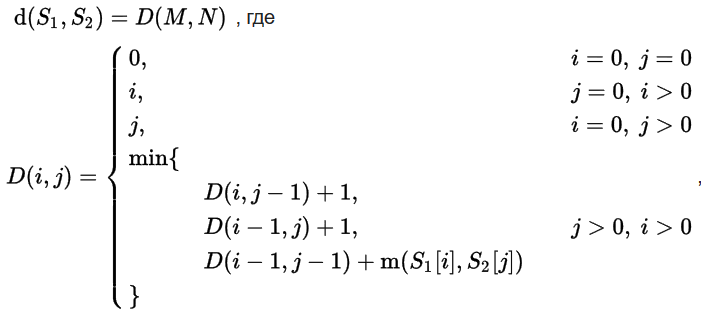
The "default implementation" of the Levenshtein algorithm was made by two mathematicians Vanger and Fisher [not to be confused with a chess player].
And it looks like in C # like this:
private Int32 levenshtein(String a, String b) { if (string.IsNullOrEmpty(a)) { if (!string.IsNullOrEmpty(b)) { return b.Length; } return 0; } if (string.IsNullOrEmpty(b)) { if (!string.IsNullOrEmpty(a)) { return a.Length; } return 0; } Int32 cost; Int32[,] d = new int[a.Length + 1, b.Length + 1]; Int32 min1; Int32 min2; Int32 min3; for (Int32 i = 0; i <= d.GetUpperBound(0); i += 1) { d[i, 0] = i; } for (Int32 i = 0; i <= d.GetUpperBound(1); i += 1) { d[0, i] = i; } for (Int32 i = 1; i <= d.GetUpperBound(0); i += 1) { for (Int32 j = 1; j <= d.GetUpperBound(1); j += 1) { cost = Convert.ToInt32(!(a[i-1] == b[j - 1])); min1 = d[i - 1, j] + 1; min2 = d[i, j - 1] + 1; min3 = d[i - 1, j - 1] + cost; d[i, j] = Math.Min(Math.Min(min1, min2), min3); } } return d[d.GetUpperBound(0), d.GetUpperBound(1)]; } Taken from here .
And visually, the work of the algorithm for the words “Prisoner” and “Dagestan” is as follows:

The extreme right-bottom corner of the matrix indicates how different the words are. From the matrix, that in this particular case, the difference between the words is 3 conditional parrots.
If it is not clear, then we will look at these words in another representation:
_ A R E S T A N T
D A G E S T A N
Thus, it turns out that in order to turn the word “Arrestant” and “Dagestan”, you need to add one letter “D”, replace one letter “P” with “G” and remove the letter “T”. Since All actions have a weight of 1, then the difference in words is 3 parrots.
If the words completely coincide, then the distance will be 0. That's the whole theory, everything ingenious is simple.
And it would seem - this is it! Everything is invented for us and there is nothing to do at all, but there is a problem ...
1) Taking weight coefficient 1 is always not quite right, because the probability of a typo depends on several specific factors: the distance of the keys on the keyboard, phonetic groups, and even the banal speed of typing.
2) The idea of Levenshtein is designed to “find differences between words,” rather than part of words, which is critical for dynamic output as letters are entered.
3) The names of the services have in their structure more than one word, then the person may simply not remember in what order they go.
We also take into account several factors, such as:
• keyboard layout in another language
• transliteration of characters
We will try to solve these problems in this article.
To begin with, let's agree that all the words we will lead to one single register. In my version of the code, I chose lower case, this will be reflected in the references that we need (these references will be given in the course of the description). In the article itself, I will resort to different writing styles, for example, “CamelCase” - ProjectArmata, but this is done solely for the convenience of human perception, from the point of view of analysis, the register is one (lower). And yet, we will take as a basis not the classical, but the optimized version of the code for finding the Levenshtein distance from here :
Adjust it a little by removing the reordering of words. For Levenshtein's algorithm, word order does not matter, but for us it will be important for other reasons. As a result, we got the following:
public int LevenshteinDistance(string source, string target){ if(String.IsNullOrEmpty(source)){ if(String.IsNullOrEmpty(target)) return 0; return target.Length; } if(String.IsNullOrEmpty(target)) return source.Length; var m = target.Length; var n = source.Length; var distance = new int[2, m + 1]; // Initialize the distance 'matrix' for(var j = 1; j <= m; j++) distance[0, j] = j; var currentRow = 0; for(var i = 1; i <= n; ++i){ currentRow = i & 1; distance[currentRow, 0] = i; var previousRow = currentRow ^ 1; for(var j = 1; j <= m; j++){ var cost = (target[j - 1] == source[i - 1] ? 0 : 1); distance[currentRow, j] = Math.Min(Math.Min( distance[previousRow, j] + 1, distance[currentRow, j - 1] + 1), distance[previousRow, j - 1] + cost); } } return distance[currentRow, m]; } Let's start improving the search algorithm with changes in weighting factors. First we make the insertion and deletion coefficients equal to 2.
Those. the lines will change:
for(var j = 1; j <= m; j++) distance[0, j] = j * 2; ... distance[currentRow, 0] = i * 2; ... distance[previousRow, j] + 2 ... distance[currentRow, j - 1] + 2 And here is the line for calculating the replacement rate of characters, we, turning into a function CostDistanceSymbol:
var cost = (target[j - 1] == source[i - 1] ? 0 : 1); And we will consider two factors:
1) Keyboard distance
2) Phonetic groups
In this regard, for more convenient work with source and target objects, we will turn them into an object:
class Word { // public string Text { get; set; } // public List<int> Codes { get; set; } = new List<int>(); } To do this, you will need the following auxiliary directories:
The ratio of key codes of the Russian keyboard:
private static SortedDictionary<char, int> CodeKeysRus = new SortedDictionary<char, int> { { '' , 192 }, { '1' , 49 }, { '2' , 50 }, ... { '-' , 189 }, { '=' , 187 }, { '' , 81 }, { '' , 87 }, { '' , 69 }, ... { '_' , 189 }, { '+' , 187 }, { ',' , 191 }, } The ratio of key codes for the English keyboard
private static SortedDictionary<char, int> CodeKeysEng = new SortedDictionary<char, int> { { '`', 192 }, { '1', 49 }, { '2', 50 }, ... { '-', 189 }, { '=', 187 }, { 'q', 81 }, { 'w', 87 }, { 'e', 69 }, { 'r', 82 }, ... { '<', 188 }, { '>', 190 }, { '?', 191 }, }; Thanks to these two reference books, mathematically speaking, we can transform two different character spaces into one single universal.
And the following relations will be fair there:
private static SortedDictionary <int, List> DistanceCodeKey = new SortedDictionary <int,
List<int>> { /* '`' */ { 192, new List<int>(){ 49 }}, /* '1' */ { 49 , new List<int>(){ 50, 87, 81 }}, /* '2' */ { 50 , new List<int>(){ 49, 81, 87, 69, 51 }}, ... /* '-' */ { 189, new List<int>(){ 48, 80, 219, 221, 187 }}, /* '+' */ { 187, new List<int>(){ 189, 219, 221 }}, /* 'q' */ { 81 , new List<int>(){ 49, 50, 87, 83, 65 }}, /* 'w' */ { 87 , new List<int>(){ 49, 81, 65, 83, 68, 69, 51, 50 }}, ... /* '>' */ { 188, new List<int>(){ 77, 74, 75, 76, 190 }}, /* '<' */ { 190, new List<int>(){ 188, 75, 76, 186, 191 }}, /* '?' */ { 191, new List<int>(){ 190, 76, 186, 222 }}, }; Those. we take the keys standing around the other key. You can verify this by the example of the figure:

Yes, I know that in addition to the QWERTY keyboard, there are other layouts, and then the table of keyboard distances will not match, but we take the most common option.
If someone knows a better way - please write.
Now we are ready for the first stage - calculating the weight of the error symbol in the CostDistanceSymbol function:
As it was before, if the characters are the same, then the distance is 0:
if (source.Text[sourcePosition] == target.Text[targetPosition]) return 0; If the key codes are the same, then the distance is also 0:
if (source.Codes[sourcePosition] != 0 && target.Codes[targetPosition] == target.Codes[targetPosition]) return 0; If you have a question why we compare key codes after comparing characters, the answer is simple - we want the words “Water” and “Djlf” to be perceived the same way. And the characters that can be typed on different layouts, for example, ";" or "," regardless of the layout, were also perceived the same way.
Further, we are only looking at the codes how closely the key codes are from each other. If close, then distance 1, and if not, then 2 (exactly the same weight as when inserting or deleting):
int resultWeight = 0; List<int> nearKeys; if (!DistanceCodeKey.TryGetValue(source.Codes[sourcePosition], out nearKeys)) resultWeight = 2; else resultWeight = nearKeys.Contains(target.Codes[searchPosition]) ? 1 : 2; In fact, such a small refinement covers a huge number of random errors ranging from the wrong layout, ending with a miss by the key.
But after the typing errors, a person simply may not know how words are spelled. For example: pike, posh. test
Such words are not only in Russian, but also in English. Similar cases we also need to take into account. For the English words, we take as a basis the work of Zobel and Dart on phonetic groups .
"Aeiouy", "bp", "ckq", "dt", "lr", "mn", "gj", "fpv", "sxz", "csz"
And for Russian, I will compile myself on a whim:
“Yiy”, “ee”, “aya”, “oee”, “yu”, “sc”, “oa”, “yo”
These phonetic groups are converted into an object of the type:
PhoneticGroupsEng = { { 'a', { 'e', 'i', 'o', 'u', 'y'} }, { 'e', { 'a', 'i', 'o', 'u', 'y'} } ... } This can be done by hand or as I write code, but the result will be the same. And now after checking the key code, you can check the letters for entering the phonetic group with the same logic of finding errors as in the previous step:
List<char> phoneticGroups; if (PhoneticGroupsRus.TryGetValue(target.Text[targetPosition], out phoneticGroups)) resultWeight = Math.Min(resultWeight, phoneticGroups.Contains(source.Text[sourcePosition]) ? 1 : 2); if (PhoneticGroupsEng.TryGetValue(target.Text[targetPosition], out phoneticGroups)) resultWeight = Math.Min(resultWeight, phoneticGroups.Contains(source.Text[sourcePosition]) ? 1 : 2); In addition to the above missed typos, there are typos "typing speed" of the text. This is when two consecutive letters people, when typing, confused places. Moreover, this is such a common mistake that a certain mathematician Frederick Damerau modified the Levenshtein algorithm by adding a transposition (permutation) of characters.
From a programmatic point of view, we add the following to the LevenshteinDistance function:

if (i > 1 && j > 1 && source.Text[i - 1] == target.Text[j - 2] && source.Text[i - 2] == target.Text[j - 1]) { distance[currentRow, j] = Math.Min(distance[currentRow, j], distance[(i - 2) % 3, j - 2] + 2); } Remark
The optimized code that we took as a basis has the following form of initialization of the distance matrix: var distance = new int [2, m + 1];
Therefore, this section of the code “distance [(i - 2)% 3, ...” will not work in its current form, I will give the correct version of the function at the end of the article.
Therefore, this section of the code “distance [(i - 2)% 3, ...” will not work in its current form, I will give the correct version of the function at the end of the article.
Thus, we have completed the first paragraph to refine the code. Go to the second paragraph. Recall that the Levenshtein idea is intended to “find differences between words,” and not part of the words, which is critical for dynamic output results as letters are entered.
For example, in the directory there are two words:
• “ProjectArmata”
• "Yak"
Entering the query “Pro” in the search bar, we get “Yak” as a higher priority, due to the fact that replacing two characters and deleting one will be only 3 parrots (taking into account unit coefficients and the classical Levenshtein algorithm, without our modifications), Adding part of the word "jectArmata" 10 parrots.
The most logical in this situation is not to compare the whole word, but only a part of the desired word with the entered string.
Since the search query consists of three characters “Pro”, we will take the first three characters from the word “ProjectArmata”, i.e. “Pro” and get 100% match. For this particular case - perfect. But let's consider some more options. Suppose we have in the database, there is the following set of words:
• "Communal"
• "Conveyor"
• "The colony"
• “Cosmetics”
The search query will look like “com”. As a result, words will have the following match factors:
Communal - 0
Conveyor - 1
Colony - 1
Cosmetics - 1
If everything is normal with the word “Kommunalka”, then the other three words look somehow uniform ... Although it is clear that, perhaps, the person described himself in one letter and he is looking for “Cosmetics”, and not Conveyor or Colony. And our task is to give him the most suitable result, and not just everything. Especially, as Damerau said - most of the errors are transpositions of letters.
To eliminate such a mistake, we do a little refinement:
Take not the first “n” letters, but “n + 1” letters, where n is the number of letters in the query. And then the coefficients when querying "Com" will be as follows:
Communal - 1
Cosmetics - 1
Conveyor - 2
Colony - 2
“Cosmetics” was corrected, but “Kommunalka” left ... But I like this option more for what reasons. Usually, if a search is required, initially the information is shown to the user in the form of a drop-down list, under the search line, as letters are entered. The length of this drop-down list is limited in size to 3-7 entries. As a consequence, if there are only three entries, then in the second version they will appear: “Communal”, “Cosmetics” and “Conveyor” [as he is stupid first in issuing because of a guid, or simply because of the date of creation]. And in the first case there will be “Communal”, “Conveyor”, “Colony” and no “Cosmetics”, since she was not lucky for other reasons ...
Of course, this problem has other solutions. For example, sort first, by “n” letters, and then, take those groups of words from whom the indices coincided and additionally re-sort the “n + 1” letters and you can again, and again ... Here it is solved individually depending on the data in the database , solvable problem, computing power.
Let's not now focus on solving the above problem ... We are only in the middle of the road and I still have something to tell.
The following nuance in the correct search results comes to us from the times of the USSR. Then they loved to make names consisting of several words combined into one. And now it is relevant:
Consumer union
GazPromBank
Agricultural Bank
ProjectArmata
BankURALSIB
Etc.
[ps I know that some of the names are separated by spaces, but I needed to pick some vivid examples]
But, if we follow our algorithm, we always take the first "n + 1" letters from the word. And if a person picks up the word "Bank", he will not receive an adequate issuance. Since we will compare the lines:
"Bank"
"Potre"
"Gazpr"
Rosse
"Proje"
To find the word "bank" regardless of position, we will need to make a floating window for the phrase and return the smallest coefficient:
double GetRangeWord(Word source, Word target) { double rangeWord = double.MaxValue; Word croppedSource = new Word(); int length = Math.Min(source.Text.Length, target.Text.Length + 1); for (int i = 0; i <= source.Text.Length - length; i++) { croppedSource.Text = target.Text.Substring(i, length); croppedSource.Codes = target.Codes.Skip(i).Take(length).ToList(); rangeWord = Math.Min(LevenshteinDistance(croppedSource, target) + (i * 2 / 10.0), rangeWord); } return rangeWord; } As you can see, to the error obtained after calculating the Levenshtein distance, we add another value (i * 2 / 10.0). If with “i * 2” everything is clear, this is a mistake of inserting letters at the beginning of a word, like the classical algorithm for finding the Levenshtein distance, but why do we divide it by 10? The bottom line is that if we just leave “i * 2”, then words that are stupidly shorter in length will fall into the issue of claim and we will again get away from the name of the banks. And so the coefficient has to be divided by 10, which is to reduce this offset. Why exactly 10? For our base, it was more or less normal, but I do not exclude that it can be divided into more. Everything depends on the length of the words and how similar the words are. I will give the calculation of the most suitable coefficient a little later.
With words, as well as the search unit, sort of sorted out, now go to the phrases. And first, again, a few examples:
• warface
• world of tanks
• world of warplanes
• world of ships
Let's understand what we basically need from searching for a phrase. We need the missing words to be added, the extra phrases deleted, and also that they change places. Somewhere I have already said this ... And, exactly, I remembered ... At the beginning of the article, when I was talking about the words and the function of Levenshtein distance. In order not to waste your time, I will immediately say that it did not work out in its pure form, but inspired by her, she managed to write code applicable to phrases.
As with the implementation of the Levenshtein distance function, if one of the phrases is empty, then we return an error value equal to the insertion or deletion [depending on which side the empty phrase came from] of all the letters.
if (!source.Words.Any()) { if (!search.Words.Any()) return 0; return search.Words.Sum(w => w.Text.Length) * 2 * 100; } if (!search.Words.Any()) { return source.Words.Sum(w => w.Text.Length) * 2 * 100; } Those. we summarize the number of letters in the phrase multiplied by 2 (this coefficient was chosen at the beginning of the article for letters) and multiplied by 100. These 100 are the most controversial coefficient in the whole algorithm. For what it will be needed more clearly presented below, and then I will explain that, in theory, it must be calculated, and not just taken from the ceiling.
double result = 0; for (int i = 0; i < search.Words.Count; i++) { double minRangeWord = double.MaxValue; int minIndex = 0; for (int j = 0; j < source.Words.Count; j++) { double currentRangeWord = GetRangeWord(source.Words[j], search.Words[i], translation); if (currentRangeWord < minRangeWord) { minRangeWord = currentRangeWord; minIndex = j; } } result += minRangeWord * 100 + (Math.Abs(i - minIndex) / 10.0); } return result; } In this code, we match each word from the record in the database with each of the search query and take the smallest coefficients for each word. The total coefficient for the phrase is as follows:
result + = minRangeWord * 100 + (Math.Abs (i - minIndex) / 10.0);
As you can see, all the logic is the same as described earlier, the minimum coefficient for the word minRangeWord is multiplied by our 100 and summed up with the coefficient that shows how close the word is to its most suitable position (Math.Abs (i - minIndex) / 10.0).
A multiplication of 100 is used to compensate for the incremental coefficient that may occur when searching for the most suitable position of the search word in the previous step. As a result, this coefficient can be calculated as the largest between the phrase in the search line and all the words in the database. Not phrases, namely words. But for this, it would be necessary to measure the Levenshtein distance with our modifications to “empty” with our modifications, which is very wasteful in terms of resources.
Those. get rid of the function GetRangeWord and take the maximum value of the deviation of the phrase “i * 2” from the most appropriate place. And then take the highest value to bring it to the nearest larger tenfold number (10, 100, 1000, 10000, 100000, etc.). Thus we get two values:
The first is the value to which the mixed word should be divided in the GetRangeWord function. The second is the value that you need to multiply minRangeWord to compensate for the previous offset. In this way we will get accurate indicators of phrase similarity. But in practice one can neglect large deviations, and estimate the average approximately ... What I actually did.
In principle, everything. The main questions I have left out are just a slight refinement of the “transliteration of characters”. The difference between the above described search and the search in transliteration is that, in the CostDistanceSymbol function, we will not adjust the response values by key distance, since The issue in this case will not be correct.
It can also be noted that the adequate output of the result begins with 3 characters in the search string; if the symbol is smaller, it is better to use a more clumsy method with accurate string matching.
Next, I will give the most complete code of all the above described, but first:
1) This code was written by me personally in my free time.
2) The algorithm was thought out by me personally in my free time.
Separately, I want to say thank you for the links and inspiration: Dmitry Panyushkin, Pavel Grigorenko.
The names that are given in the article are taken from public sources and belong to their owners. Not an advertisement.
Thanks to everyone who read. Criticism and advice are welcome.
Full code
public class DistanceAlferov { class Word { public string Text { get; set; } public List<int> Codes { get; set; } = new List<int>(); } class AnalizeObject { public string Origianl { get; set; } public List<Word> Words { get; set; } = new List<Word>(); } class LanguageSet { public AnalizeObject Rus { get; set; } = new AnalizeObject(); public AnalizeObject Eng { get; set; } = new AnalizeObject(); } List<LanguageSet> Samples { get; set; } = new List<LanguageSet>(); public void SetData(List<Tuple<string, string>> datas) { List<KeyValuePair<char, int>> codeKeys = CodeKeysRus.Concat(CodeKeysEng).ToList(); foreach (var data in datas) { LanguageSet languageSet = new LanguageSet(); languageSet.Rus.Origianl = data.Item1; if (data.Item1.Length > 0) { languageSet.Rus.Words = data.Item1.Split(' ').Select(w => new Word() { Text = w.ToLower(), Codes = GetKeyCodes(codeKeys, w) }).ToList(); } languageSet.Eng.Origianl = data.Item2; if (data.Item2.Length > 0) { languageSet.Eng.Words = data.Item2.Split(' ').Select(w => new Word() { Text = w.ToLower(), Codes = GetKeyCodes(codeKeys, w) }).ToList(); } this.Samples.Add(languageSet); } } public List<Tuple<string, string, double, int>> Search(string targetStr) { List<KeyValuePair<char, int>> codeKeys = CodeKeysRus.Concat(CodeKeysEng).ToList(); AnalizeObject originalSearchObj = new AnalizeObject(); if (targetStr.Length > 0) { originalSearchObj.Words = targetStr.Split(' ').Select(w => new Word() { Text = w.ToLower(), Codes = GetKeyCodes(codeKeys, w) }).ToList(); } AnalizeObject translationSearchObj = new AnalizeObject(); if (targetStr.Length > 0) { translationSearchObj.Words = targetStr.Split(' ').Select(w => { string translateStr = Transliterate(w.ToLower(), Translit_Ru_En); return new Word() { Text = translateStr, Codes = GetKeyCodes(codeKeys, translateStr) }; }).ToList(); } var result = new List<Tuple<string, string, double, int>>(); foreach (LanguageSet sampl in Samples) { int languageType = 1; double cost = GetRangePhrase(sampl.Rus, originalSearchObj, false); double tempCost = GetRangePhrase(sampl.Eng, originalSearchObj, false); if (cost > tempCost) { cost = tempCost; languageType = 3; } // tempCost = GetRangePhrase(sampl.Rus, translationSearchObj, true); if (cost > tempCost) { cost = tempCost; languageType = 2; } tempCost = GetRangePhrase(sampl.Eng, translationSearchObj, true); if (cost > tempCost) { cost = tempCost; languageType = 3; } result.Add(new Tuple<string, string, double, int>(sampl.Rus.Origianl, sampl.Eng.Origianl, cost, languageType)); } return result; } private double GetRangePhrase(AnalizeObject source, AnalizeObject search, bool translation) { if (!source.Words.Any()) { if (!search.Words.Any()) return 0; return search.Words.Sum(w => w.Text.Length) * 2 * 100; } if (!search.Words.Any()) { return source.Words.Sum(w => w.Text.Length) * 2 * 100; } double result = 0; for (int i = 0; i < search.Words.Count; i++) { double minRangeWord = double.MaxValue; int minIndex = 0; for (int j = 0; j < source.Words.Count; j++) { double currentRangeWord = GetRangeWord(source.Words[j], search.Words[i], translation); if (currentRangeWord < minRangeWord) { minRangeWord = currentRangeWord; minIndex = j; } } result += minRangeWord * 100 + (Math.Abs(i - minIndex) / 10.0); } return result; } private double GetRangeWord(Word source, Word target, bool translation) { double minDistance = double.MaxValue; Word croppedSource = new Word(); int length = Math.Min(source.Text.Length, target.Text.Length + 1); for (int i = 0; i <= source.Text.Length - length; i++) { croppedSource.Text = source.Text.Substring(i, length); croppedSource.Codes = source.Codes.Skip(i).Take(length).ToList(); minDistance = Math.Min(minDistance, LevenshteinDistance(croppedSource, target, croppedSource.Text.Length == source.Text.Length, translation) + (i * 2 / 10.0)); } return minDistance; } private int LevenshteinDistance(Word source, Word target, bool fullWord, bool translation) { if (String.IsNullOrEmpty(source.Text)) { if (String.IsNullOrEmpty(target.Text)) return 0; return target.Text.Length * 2; } if (String.IsNullOrEmpty(target.Text)) return source.Text.Length * 2; int n = source.Text.Length; int m = target.Text.Length; //TODO ( ) int[,] distance = new int[3, m + 1]; // Initialize the distance 'matrix' for (var j = 1; j <= m; j++) distance[0, j] = j * 2; var currentRow = 0; for (var i = 1; i <= n; ++i) { currentRow = i % 3; var previousRow = (i - 1) % 3; distance[currentRow, 0] = i * 2; for (var j = 1; j <= m; j++) { distance[currentRow, j] = Math.Min(Math.Min( distance[previousRow, j] + ((!fullWord && i == n) ? 2 - 1 : 2), distance[currentRow, j - 1] + ((!fullWord && i == n) ? 2 - 1 : 2)), distance[previousRow, j - 1] + CostDistanceSymbol(source, i - 1, target, j - 1, translation)); if (i > 1 && j > 1 && source.Text[i - 1] == target.Text[j - 2] && source.Text[i - 2] == target.Text[j - 1]) { distance[currentRow, j] = Math.Min(distance[currentRow, j], distance[(i - 2) % 3, j - 2] + 2); } } } return distance[currentRow, m]; } private int CostDistanceSymbol(Word source, int sourcePosition, Word search, int searchPosition, bool translation) { if (source.Text[sourcePosition] == search.Text[searchPosition]) return 0; if (translation) return 2; if (source.Codes[sourcePosition] != 0 && source.Codes[sourcePosition] == search.Codes[searchPosition]) return 0; int resultWeight = 0; List<int> nearKeys; if (!DistanceCodeKey.TryGetValue(source.Codes[sourcePosition], out nearKeys)) resultWeight = 2; else resultWeight = nearKeys.Contains(search.Codes[searchPosition]) ? 1 : 2; List<char> phoneticGroups; if (PhoneticGroupsRus.TryGetValue(search.Text[searchPosition], out phoneticGroups)) resultWeight = Math.Min(resultWeight, phoneticGroups.Contains(source.Text[sourcePosition]) ? 1 : 2); if (PhoneticGroupsEng.TryGetValue(search.Text[searchPosition], out phoneticGroups)) resultWeight = Math.Min(resultWeight, phoneticGroups.Contains(source.Text[sourcePosition]) ? 1 : 2); return resultWeight; } private List<int> GetKeyCodes(List<KeyValuePair<char, int>> codeKeys, string word) { return word.ToLower().Select(ch => codeKeys.FirstOrDefault(ck => ck.Key == ch).Value).ToList(); } private string Transliterate(string text, Dictionary<char, string> cultureFrom) { IEnumerable<char> translateText = text.SelectMany(t => { string translateChar; if (cultureFrom.TryGetValue(t, out translateChar)) return translateChar; return t.ToString(); }); return string.Concat(translateText); } #region static Dictionary<char, List<char>> PhoneticGroupsRus = new Dictionary<char, List<char>>(); static Dictionary<char, List<char>> PhoneticGroupsEng = new Dictionary<char, List<char>>(); #endregion static DistanceAlferov() { SetPhoneticGroups(PhoneticGroupsRus, new List<string>() { "", "", "", "", "", "", "" }); SetPhoneticGroups(PhoneticGroupsEng, new List<string>() { "aeiouy", "bp", "ckq", "dt", "lr", "mn", "gj", "fpv", "sxz", "csz" }); } private static void SetPhoneticGroups(Dictionary<char, List<char>> resultPhoneticGroups, List<string> phoneticGroups) { foreach (string group in phoneticGroups) foreach (char symbol in group) if (!resultPhoneticGroups.ContainsKey(symbol)) resultPhoneticGroups.Add(symbol, phoneticGroups.Where(pg => pg.Contains(symbol)).SelectMany(pg => pg).Distinct().Where(ch => ch != symbol).ToList()); } #region /// <summary> /// /// </summary> private static Dictionary<int, List<int>> DistanceCodeKey = new Dictionary<int, List<int>> { /* '`' */ { 192 , new List<int>(){ 49 }}, /* '1' */ { 49 , new List<int>(){ 50, 87, 81 }}, /* '2' */ { 50 , new List<int>(){ 49, 81, 87, 69, 51 }}, /* '3' */ { 51 , new List<int>(){ 50, 87, 69, 82, 52 }}, /* '4' */ { 52 , new List<int>(){ 51, 69, 82, 84, 53 }}, /* '5' */ { 53 , new List<int>(){ 52, 82, 84, 89, 54 }}, /* '6' */ { 54 , new List<int>(){ 53, 84, 89, 85, 55 }}, /* '7' */ { 55 , new List<int>(){ 54, 89, 85, 73, 56 }}, /* '8' */ { 56 , new List<int>(){ 55, 85, 73, 79, 57 }}, /* '9' */ { 57 , new List<int>(){ 56, 73, 79, 80, 48 }}, /* '0' */ { 48 , new List<int>(){ 57, 79, 80, 219, 189 }}, /* '-' */ { 189 , new List<int>(){ 48, 80, 219, 221, 187 }}, /* '+' */ { 187 , new List<int>(){ 189, 219, 221 }}, /* 'q' */ { 81 , new List<int>(){ 49, 50, 87, 83, 65 }}, /* 'w' */ { 87 , new List<int>(){ 49, 81, 65, 83, 68, 69, 51, 50 }}, /* 'e' */ { 69 , new List<int>(){ 50, 87, 83, 68, 70, 82, 52, 51 }}, /* 'r' */ { 82 , new List<int>(){ 51, 69, 68, 70, 71, 84, 53, 52 }}, /* 't' */ { 84 , new List<int>(){ 52, 82, 70, 71, 72, 89, 54, 53 }}, /* 'y' */ { 89 , new List<int>(){ 53, 84, 71, 72, 74, 85, 55, 54 }}, /* 'u' */ { 85 , new List<int>(){ 54, 89, 72, 74, 75, 73, 56, 55 }}, /* 'i' */ { 73 , new List<int>(){ 55, 85, 74, 75, 76, 79, 57, 56 }}, /* 'o' */ { 79 , new List<int>(){ 56, 73, 75, 76, 186, 80, 48, 57 }}, /* 'p' */ { 80 , new List<int>(){ 57, 79, 76, 186, 222, 219, 189, 48 }}, /* '[' */ { 219 , new List<int>(){ 48, 186, 222, 221, 187, 189 }}, /* ']' */ { 221 , new List<int>(){ 189, 219, 187 }}, /* 'a' */ { 65 , new List<int>(){ 81, 87, 83, 88, 90 }}, /* 's' */ { 83 , new List<int>(){ 81, 65, 90, 88, 67, 68, 69, 87, 81 }}, /* 'd' */ { 68 , new List<int>(){ 87, 83, 88, 67, 86, 70, 82, 69 }}, /* 'f' */ { 70 , new List<int>(){ 69, 68, 67, 86, 66, 71, 84, 82 }}, /* 'g' */ { 71 , new List<int>(){ 82, 70, 86, 66, 78, 72, 89, 84 }}, /* 'h' */ { 72 , new List<int>(){ 84, 71, 66, 78, 77, 74, 85, 89 }}, /* 'j' */ { 74 , new List<int>(){ 89, 72, 78, 77, 188, 75, 73, 85 }}, /* 'k' */ { 75 , new List<int>(){ 85, 74, 77, 188, 190, 76, 79, 73 }}, /* 'l' */ { 76 , new List<int>(){ 73, 75, 188, 190, 191, 186, 80, 79 }}, /* ';' */ { 186 , new List<int>(){ 79, 76, 190, 191, 222, 219, 80 }}, /* '\''*/ { 222 , new List<int>(){ 80, 186, 191, 221, 219 }}, /* 'z' */ { 90 , new List<int>(){ 65, 83, 88 }}, /* 'x' */ { 88 , new List<int>(){ 90, 65, 83, 68, 67 }}, /* 'c' */ { 67 , new List<int>(){ 88, 83, 68, 70, 86 }}, /* 'v' */ { 86 , new List<int>(){ 67, 68, 70, 71, 66 }}, /* 'b' */ { 66 , new List<int>(){ 86, 70, 71, 72, 78 }}, /* 'n' */ { 78 , new List<int>(){ 66, 71, 72, 74, 77 }}, /* 'm' */ { 77 , new List<int>(){ 78, 72, 74, 75, 188 }}, /* '<' */ { 188 , new List<int>(){ 77, 74, 75, 76, 190 }}, /* '>' */ { 190 , new List<int>(){ 188, 75, 76, 186, 191 }}, /* '?' */ { 191 , new List<int>(){ 190, 76, 186, 222 }}, }; /// <summary> /// /// </summary> private static Dictionary<char, int> CodeKeysRus = new Dictionary<char, int> { { '' , 192 }, { '1' , 49 }, { '2' , 50 }, { '3' , 51 }, { '4' , 52 }, { '5' , 53 }, { '6' , 54 }, { '7' , 55 }, { '8' , 56 }, { '9' , 57 }, { '0' , 48 }, { '-' , 189 }, { '=' , 187 }, { '' , 81 }, { '' , 87 }, { '' , 69 }, { '' , 82 }, { '' , 84 }, { '' , 89 }, { '' , 85 }, { '' , 73 }, { '' , 79 }, { '' , 80 }, { '' , 219 }, { '' , 221 }, { '' , 65 }, { '' , 83 }, { '' , 68 }, { '' , 70 }, { '' , 71 }, { '' , 72 }, { '' , 74 }, { '' , 75 }, { '' , 76 }, { '' , 186 }, { '' , 222 }, { '' , 90 }, { '' , 88 }, { '' , 67 }, { '' , 86 }, { '' , 66 }, { '' , 78 }, { '' , 77 }, { '' , 188 }, { '' , 190 }, { '.' , 191 }, { '!' , 49 }, { '"' , 50 }, { '№' , 51 }, { ';' , 52 }, { '%' , 53 }, { ':' , 54 }, { '?' , 55 }, { '*' , 56 }, { '(' , 57 }, { ')' , 48 }, { '_' , 189 }, { '+' , 187 }, { ',' , 191 }, }; /// <summary> /// /// </summary> private static Dictionary<char, int> CodeKeysEng = new Dictionary<char, int> { { '`', 192 }, { '1', 49 }, { '2', 50 }, { '3', 51 }, { '4', 52 }, { '5', 53 }, { '6', 54 }, { '7', 55 }, { '8', 56 }, { '9', 57 }, { '0', 48 }, { '-', 189 }, { '=', 187 }, { 'q', 81 }, { 'w', 87 }, { 'e', 69 }, { 'r', 82 }, { 't', 84 }, { 'y', 89 }, { 'u', 85 }, { 'i', 73 }, { 'o', 79 }, { 'p', 80 }, { '[', 219 }, { ']', 221 }, { 'a', 65 }, { 's', 83 }, { 'd', 68 }, { 'f', 70 }, { 'g', 71 }, { 'h', 72 }, { 'j', 74 }, { 'k', 75 }, { 'l', 76 }, { ';', 186 }, { '\'', 222 }, { 'z', 90 }, { 'x', 88 }, { 'c', 67 }, { 'v', 86 }, { 'b', 66 }, { 'n', 78 }, { 'm', 77 }, { ',', 188 }, { '.', 190 }, { '/', 191 }, { '~' , 192 }, { '!' , 49 }, { '@' , 50 }, { '#' , 51 }, { '$' , 52 }, { '%' , 53 }, { '^' , 54 }, { '&' , 55 }, { '*' , 56 }, { '(' , 57 }, { ')' , 48 }, { '_' , 189 }, { '+' , 187 }, { '{', 219 }, { '}', 221 }, { ':', 186 }, { '"', 222 }, { '<', 188 }, { '>', 190 }, { '?', 191 }, }; #endregion #region /// <summary> /// => ASCII (ISO 9-95) /// </summary> private static Dictionary<char, string> Translit_Ru_En = new Dictionary<char, string> { { '', "a" }, { '', "b" }, { '', "v" }, { '', "g" }, { '', "d" }, { '', "e" }, { '', "yo" }, { '', "zh" }, { '', "z" }, { '', "i" }, { '', "i" }, { '', "k" }, { '', "l" }, { '', "m" }, { '', "n" }, { '', "o" }, { '', "p" }, { '', "r" }, { '', "s" }, { '', "t" }, { '', "u" }, { '', "f" }, { '', "x" }, { '', "c" }, { '', "ch" }, { '', "sh" }, { '', "shh" }, { '', "" }, { '', "y" }, { '', "'" }, { '', "e" }, { '', "yu" }, { '', "ya" }, }; #endregion } Vitaly Alferov, 2017
Source: https://habr.com/ru/post/331174/
All Articles