Below we will talk about the old woman recursion, which would be nice to represent, understand and use.

Note: This short article is written to give you a quick look at recursion, some examples of its use and hazards.

Definition

For a start it is worth saying that recursion is not only about programming. Recursion is a general concept that can be inherent in anything and occur in everyday life, but most of all it is common in computer science and mathematics. For programmers, the ability to apply recursion is a big plus in a collection of useful skills.

The biggest folly is doing the same thing and hoping for a different result.

Recursion is the process of repeating elements in a self-similar way. An object has recursion if it is part of itself.

A special case of recursion is tail recursion . If any recursive call is the last operation before returning from a function, then this is it.

Some examples

Recursion should be understood, and the definition for this is worse than visual examples. For a better understanding, of course, one should still read the definition, look at the example, read the definition again, and look at the example again ... Repeat until awareness comes.

You can find a great example here .

The most famous application of recursion to a programmer is the task of calculating Fibonacci numbers or factorial. Let's show how to implement this in C:

int fib(int n) { if (n == 0) return 0; if (n == 1 || n == 2) return 1; return fib(n - 1) + fib(n - 2); } 

 fib(1,1):-!. fib(2,1):-!. fib(N,R):- N1 is N-1, fib(N1, R1), N2 is N-2, fib(N2, R2), R is R1 + R2. 

 int factorial_rec(int n, int res) { if (n == 0) return res; return factorial_rec(n - 1, res * n); } int factorial(int n) { return factorial_rec(n, 1); } 

  #include <unistd.h> int main() { while(true) fork(); } 

For mathematics, the first association is likely to be a fractal. Fractals are beautiful and pleasing to the eye show the properties of self-similarity.

The most famous fractals:

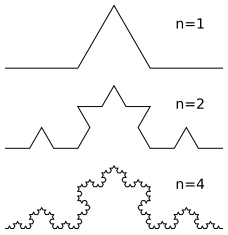
Well, in everyday life a classic example are two mirrors set opposite each other.

Go deeper

Is recursion simple? Definitely not. It looks like everything is simple, but the recursion is fraught with danger (And sometimes it is just not clear).

Let's return to the example of calculating Fibonacci numbers. Immediately, we note that the return result of the function is a call to the same function, or more precisely, the sum of the results of calling two functions (which is why recursion is not tail). It becomes clear that the second call will not occur until the first call ends (in which there will also be a call to two functions). Immediately, the inquiring mind will notice that there must be a “normal” exit from the recursive function, without making a call, otherwise we will become familiar with the call stack overflow — this is one of the key points to keep in mind when working with self-invoking functions.

Note that the call tree will be large, but the maximum number of calls in the stack will be noticeably less (N-1 for N> 2, respectively).

Recursive algorithms are quite often encountered when working with trees, sorting, and tasks on graphs. So, in order to get a better insight into practice, the above mentioned is not well suited (in particular, binary or common trees. Their implementation is not so difficult, and the experience with recursion will not turn out bad).

In addition, I would like to mention the towers of Hanoi , which are also perfect for learning about recursive tasks. Habré also had an excellent analysis of this game.

For the sake of completeness, the fight against recursion must be mentioned.

Why fight it?

Increased productivity. But this does not mean that it is simply necessary to fight it, because the use of recursion is more obvious, simpler and more pleasant than iterative options.

Is it possible to overcome any recursion?

Definitely yes. Any recursive algorithm can be rewritten without using recursion, and tail recursion is very easy to translate into iteration (which is what some compilers do for optimization). This also applies to iterative algorithms.

The most famous way is to use the stack. Here is more, for those interested.

Conclusion

Thank you for reading the article. I hope that the majority of those not familiar with recursion got a basic idea about it, but from knowledgeable people, of course, I would like to hear additions and comments in the comments. Do not be afraid of recursion and do not overflow the stack!

UPD: Added a valid tail recursion example.