3D Rose by Monte Carlo

In this article, Roman Cortes hopes to inspire readers interested in computer graphics to experiment and have fun with various visualization techniques.



Roman Cortes for the love contest 2012 js1k made a 3D rose on javascript (canvas) using the Monte Carlo method.

')

Briefly about the Monte Carlo method

The Monte-Karlo method is a general name for a group of numerical methods based on obtaining a large number of realizations of a stochastic (random) process, which is formed in such a way that its probabilistic characteristics coincide with similar values ​​of the problem being solved. It is used to solve problems in various fields of physics, chemistry, mathematics, economics, optimization, control theory, etc.

Surface rendering

To determine the shape of a rose, we will use several surfaces. In total, there are 31 surfaces: 24 petals, 4 sepals (thin leaves around the petals), 2 leaves and 1 rose stalk.



2d example of a surface detection function:

function surface(a, b) { // I'm using a and b as parameters ranging from 0 to 1. return { x: a*50, y: b*50 }; // this surface will be a square of 50x50 units of size } 

Drawing code:

 var canvas = document.body.appendChild(document.createElement("canvas")), context = canvas.getContext("2d"), a, b, position; // Now I'm going to sample the surface at .1 intervals for a and b parameters: for (a = 0; a < 1; a += .1) { for (b = 0; b < 1; b += .1) { position = surface(a, b); context.fillRect(position.x, position.y, 1, 1); } } 

Result:





Now we will reduce the interval of these pixels for a more dense image.





This allows you to override the surface function for drawing a circle. There are several ways to do this, but we will use the following formula: (x-x0) ^ 2 + (y-y0) ^ 2 <radius ^ 2, where (x0, y0) is the center of the circle:

 function surface(a, b) { var x = a * 100, y = b * 100, radius = 50, x0 = 50, y0 = 50; if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) { // inside the circle return { x: x, y: y }; } else { // outside the circle return null; } } 

In order not to draw points outside the circle, add a condition:

 if (position = surface(a, b)) { context.fillRect(position.x, position.y, 1, 1); } 

We get:





As already mentioned, there are various ways to define a circle, and we need to show it only in one direction:

 function surface(a, b) { // Circle using polar coordinates var angle = a * Math.PI * 2, radius = 50, x0 = 50, y0 = 50; return { x: Math.cos(angle) * radius * b + x0, y: Math.sin(angle) * radius * b + y0 }; } 

The following function allows us to deform a circle to make it look like a petal:

 function surface(a, b) { var x = a * 100, y = b * 100, radius = 50, x0 = 50, y0 = 50; if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) { return { x: x, y: y * (1 + b) / 2 // deformation }; } else { return null; } } 

I want to add some color:

 function surface(a, b) { var x = a * 100, y = b * 100, radius = 50, x0 = 50, y0 = 50; if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) { return { x: x, y: y * (1 + b) / 2, r: 100 + Math.floor((1 - b) * 155), // this will add a gradient g: 50, b: 50 }; } else { return null; } } for (a = 0; a < 1; a += .01) { for (b = 0; b < 1; b += .001) { if (point = surface(a, b)) { context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")"; context.fillRect(point.x, point.y, 1, 1); } } } 

Petals are ready!

3D surface and perspective projection

Making a 3D surface is very simple: just add az properties to the surface. As an example, let's make a pipe / cylinder:

 function surface(a, b) { var angle = a * Math.PI * 2, radius = 100, length = 400; return { x: Math.cos(angle) * radius, y: Math.sin(angle) * radius, z: b * length - length / 2, // by subtracting length/2 I have centered the tube at (0, 0, 0) r: 0, g: Math.floor(b * 255), b: 0 }; } 

To add perspective to the projection, you must determine the position of the camera.





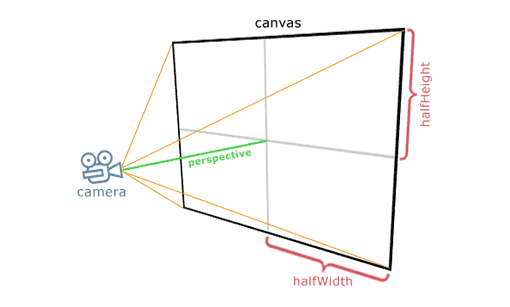
We will make the camera at the point (0, 0, cameraZ), it will be called “perspective” - the distance from the camera to the canvas. The center will be at the point (0, 0, cameraZ + perspective). Now each point will be projected on the canvas:

 var pX, pY, // projected on canvas x and y coordinates perspective = 350, halfHeight = canvas.height / 2, halfWidth = canvas.width / 2, cameraZ = -700; for (a = 0; a < 1; a += .001) { for (b = 0; b < 1; b += .01) { if (point = surface(a, b)) { pX = (point.x * perspective) / (point.z - cameraZ) + halfWidth; pY = (point.y * perspective) / (point.z - cameraZ) + halfHeight; context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")"; context.fillRect(pX, pY, 1, 1); } } } 

Result:

Z-buffer

Z-buffer is a fairly common technology in the field of computer graphics to account for the distance of image elements.







This can be seen on the Z-buffer of the rose: the black element is far from the camera, white is close to it.



Implementation:

 var zBuffer = [], zBufferIndex; for (a = 0; a < 1; a += .001) { for (b = 0; b < 1; b += .01) { if (point = surface(a, b)) { pX = Math.floor((point.x * perspective) / (point.z - cameraZ) + halfWidth); pY = Math.floor((point.y * perspective) / (point.z - cameraZ) + halfHeight); zBufferIndex = pY * canvas.width + pX; if ((typeof zBuffer[zBufferIndex] === "undefined") || (point.z < zBuffer[zBufferIndex])) { zBuffer[zBufferIndex] = point.z; context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")"; context.fillRect(pX, pY, 1, 1); } } } } 

Cylinder rotation

You can use any method of rotation vector. In the case of the rose, but here we use the Euler rotation theorem . Let's implement rotation around the Y axis:

 function surface(a, b) { var angle = a * Math.PI * 2, radius = 100, length = 400, x = Math.cos(angle) * radius, y = Math.sin(angle) * radius, z = b * length - length / 2, yAxisRotationAngle = -.4, // in radians! rotatedX = x * Math.cos(yAxisRotationAngle) + z * Math.sin(yAxisRotationAngle), rotatedZ = x * -Math.sin(yAxisRotationAngle) + z * Math.cos(yAxisRotationAngle); return { x: rotatedX, y: y, z: rotatedZ, r: 0, g: Math.floor(b * 255), b: 0 }; } 

Result:

Monte Carlo method

 var i; window.setInterval(function () { for (i = 0; i < 10000; i++) { if (point = surface(Math.random(), Math.random())) { pX = Math.floor((point.x * perspective) / (point.z - cameraZ) + halfWidth); pY = Math.floor((point.y * perspective) / (point.z - cameraZ) + halfHeight); zBufferIndex = pY * canvas.width + pX; if ((typeof zBuffer[zBufferIndex] === "undefined") || (point.z < zBuffer[zBufferIndex])) { zBuffer[zBufferIndex] = point.z; context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")"; context.fillRect(pX, pY, 1, 1); } } } }, 0); 

Conclusion

To complete the rose, I had to add a third parameter for the function that selects a part of the rose. In the case of petals, we use rotations and extensions / deformations. All this is done by mixing, which are described in this article.



The choice of Monte Carlo / Z-buffering fell for artistic purposes. Not a very innovative and not very useful script, but it fits very well into the js1k context, where simplicity and minimal sizes are desirable.



I can not believe that the whole rose can be in this code:

 <!doctype html> <html> <head> <title>JS1k, 1k demo submission [1022]</title> <meta charset="utf-8" /> </head> <body> <canvas id="c"></canvas> <script> var b = document.body; var c = document.getElementsByTagName('canvas')[0]; var a = c.getContext('2d'); document.body.clientWidth; // fix bug in webkit: http://qfox.nl/weblog/218 </script> <script> // start of submission // with(m=Math)C=cos,S=sin,P=pow,R=random;c.width=c.height=f=500;h=-250;function p(a,b,c){if(c>60)return[S(a*7)*(13+5/(.2+P(b*4,4)))-S(b)*50,b*f+50,625+C(a*7)*(13+5/(.2+P(b*4,4)))+b*400,a*1-b/2,a];A=a*2-1;B=b*2-1;if(A*A+B*B<1){if(c>37){n=(j=c&1)?6:4;o=.5/(a+.01)+C(b*125)*3-a*300;w=b*h;return[o*C(n)+w*S(n)+j*610-390,o*S(n)-w*C(n)+550-j*350,1180+C(B+A)*99-j*300,.4-a*.1+P(1-B*B,-h*6)*.15-a*b*.4+C(a+b)/5+P(C((o*(a+1)+(B>0?w:-w))/25),30)*.1*(1-B*B),o/1e3+.7-o*w*3e-6]}if(c>32){c=c*1.16-.15;o=a*45-20;w=b*b*h;z=o*S(c)+w*C(c)+620;return[o*C(c)-w*S(c),28+C(B*.5)*99-b*b*b*60-z/2-h,z,(b*b*.3+P((1-(A*A)),7)*.15+.3)*b,b*.7]}o=A*(2-b)*(80-c*2);w=99-C(A)*120-C(b)*(-hc*4.9)+C(P(1-b,7))*50+c*2;z=o*S(c)+w*C(c)+700;return[o*C(c)-w*S(c),B*99-C(P(b, 7))*50-c/3-z/1.35+450,z,(1-b/1.2)*.9+a*.1, P((1-b),20)/4+.05]}}setInterval('for(i=0;i<1e4;i++)if(s=p(R(),R(),i%46/.74)){z=s[2];x=~~(s[0]*f/zh);y=~~(s[1]*f/zh);if(!m[q=y*f+x]|m[q]>z)m[q]=z,a.fillStyle="rgb("+~(s[3]*h)+","+~(s[4]*h)+","+~(s[3]*s[3]*-80)+")",a.fillRect(x,y,1,1)}',0) // end of submission // </script> </body> </html>