Electronic digital signature for dummies: what it is and how not to choke. Part 3
Part 1
Part 2
In this part we will make a small digression from digital signatures in the direction of that, without which directly digital signatures, and even the protection of information in the usual sense, would not be: encryption. After all, the first thing that comes to mind when it comes to protecting our data is not to give this data to a bad person to read. Therefore, before continuing to examine the standards of PGP and S / MIME, it is worth painting out some white spots that remain in knowledge, and consider the encryption process in a bit more detail.
Ciphers and codes exist, probably, from the moment humanity learned to record their impressions of the world around us on media. If you think about it a little, even an ordinary alphabet is already a cipher. After all, when we read a text, in our head a certain sound, a combination of sounds, or even a whole concept is compared to each character, and this does not happen in the head of a neighbor who does not know how to read.
')
Without knowing which symbol and what is matched, we can never understand what exactly the writer had in mind. For example, try to take and read something written in Hebrew or in Chinese. The alphabets of these languages themselves will be an insurmountable obstacle for you, even if the concepts of your native language are written with the help of these symbols.
But, nevertheless, the mere use of someone else's alphabet is still insufficient measure to protect your data. After all, any alphabet, anyway, was created for ease of use and is inextricably linked with the language to which this alphabet is characteristic. So, having learned this language and some set of basic concepts on it (or even just using the services of a person who knows the given language), a bad person can read your information.
So, we need to come up with an alphabet that knows only a limited circle of people, and use it to record information. Surely everyone read (or at least heard) a cycle of stories about Sherlock Holmes. This cycle featured an alphabet made up of dancing little men (and many, I think, made up their own based on it in childhood). However, as this story shows, an observant person can figure out which symbol belongs to what. So our information will again fall into the wrong hands.
What to do? Come up with more and more complex alphabets? But the more complex and cumbersome the alphabet, the more inconvenient it is to work with it, to keep it secret. In addition, there is a wonderful proverb about mystery: two people know - everyone knows. After all, the weakest link in any cipher is a person who knows how to decrypt this cipher.
And why not make it so that the encryption method is immediately known to everyone, but it would be impossible to decrypt our data without some kind of key? After all, the key (unlike the entire alphabet) is small, it is easy enough to make a new one, if that (again, unlike the processing of the entire alphabet), it is easy to hide. The most vividly the advantages of key systems are shown by the following example: the recipient needs to read the message you sent. Plain, on paper. Let's say you use a secret alphabet. Then, in order to read the message, the recipient must know the alphabet, have a large dusty Talmud, which describes how to decrypt (after all, the alphabet must be complicated to be reliable) and understand how to work with this Talmud. With keys, everything is simpler: you put the message in a box with a lock, and the recipient simply inserts a suitable key, and you need to know how the lock works.
So, the well-known "alphabets" and keys - a mechanism that is much more convenient than just alphabets. But how to encrypt so that everything is decrypted with a simple key? And this is where mathematics comes to the rescue, and more specifically, mathematical functions that can be used to replace our original symbols with new ones.
Recall what a function is. This is some relation by which from one number you can get another. Knowing x and substituting it into the known relation y = A * x, we always get the value of y. But, as a rule, the opposite is also true: knowing y, we can also get x.
As a rule, but not always. For many dependencies, getting y is easy, whereas x is already very difficult, and getting it will take a long time. It is precisely on such dependencies that the encryption used now is based.
But back to encryption itself. Encryption is divided into symmetric , asymmetric, and combined . Consider the essence of each of them.
Symmetric encryption , by and large, is quite slightly different from the good old secret alphabet. As a matter of fact, it differs just in the presence of a key - some relatively small sequence of numbers, which is used for encryption and decryption. At the same time, each of the parties exchanging information should know this key and keep it secret. A huge advantage of this approach is the encryption speed: the key, in fact, is a fairly simple and short instruction, which symbol, when, and with which to replace. And this key works in both directions (that is, with it you can both replace all the characters with new ones, and return everything as it was), for which this encryption method was called symmetric. Equally a huge disadvantage is the fact that both parties, between which information is sent, must know the key. At the same time, it is worth it for a bad person to get the key, as he immediately reads our carefully protected data, which means the problem of handing over the key to the receiving party becomes full length.
Asymmetric encryption comes a little trickier. Here both we and our recipient already have two keys that are called open and closed. We also keep the recipient's private key (note that everyone only keeps his own key, which means we’re already going beyond the very same proverb about the two who know), and we can safely transfer the public key to anyone — our private, secret, it can not be restored. Total, we use the recipient's public key for encryption, and the recipient, in turn, uses his private key to decrypt. The advantage of this approach is obvious: we can easily start sharing secret information with different recipients, practically nothing (assuming that our recipient did not lose / give away his private key, etc., that is, did not transfer it into the hands of a bad person) when transmitting information. But, without a huge minus is not enough. And here it is as follows: in this case, encryption and decryption go very, very, very slowly, two or three orders of magnitude slower than similar operations with symmetric encryption. In addition, resources for this encryption is also spent much more. And the keys themselves for these operations are significantly longer than those for symmetric encryption operations, since it is necessary to secure the private key as much as possible from matching the public key. So, it is simply unprofitable to encrypt large amounts of information in this way.
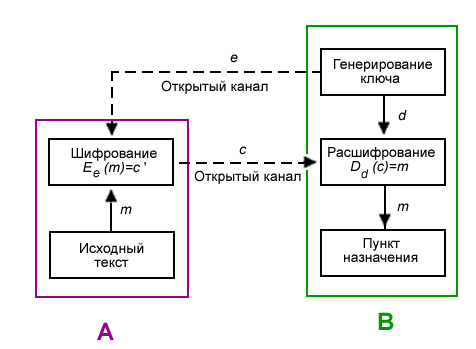
An example of using asymmetric encryption [Wikipedia]
e - recipient's public key B
d - recipient's private key B
m - the source information of the sender A
c - encrypted source information
And again the question arises: what to do? And you need to do the following: take and combine both methods. Actually, this is how we get the combined encryption. We will encrypt our large amount of data using the first method, and in order to convey the key with which we encrypted them to the recipient, we will encrypt the key using the second method. Then we get that even though asymmetric encryption is slow, the volume of encrypted data (that is, the key on which large data is encrypted) will be small, which means that decryption will pass fairly quickly, and more rapid symmetric encryption will come in later.
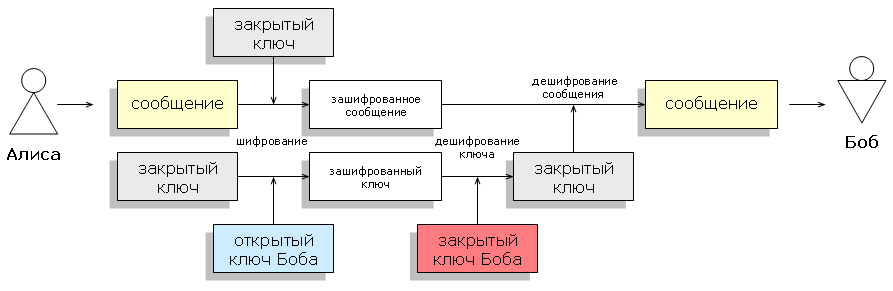
An example of the use of the combined system [Wikipedia]
All these mechanisms have been applied in practice, and both of our large camps PGP and S / MIME use them. As stated in the first article, asymmetric encryption is used to digitally sign (that is, to encrypt our hash). The difference of this application from the usual asymmetric encryption is that our private key is used for encryption, and for decryption, the presence of the public key associated with it is sufficient. Since we don’t hide the public key, our hash can be read by anyone, not just the individual recipient, which is required for a digital signature.
Combined encryption is used in both standards directly to encrypt the data sent.
Thus, starting to use digital signatures to protect our data from being tampered with, we automatically (for these two standards) also get a wonderful opportunity to protect our data from reading as well, which you will agree is very convenient.
Now that we have become familiar with the general principles of the mechanisms used to protect our data, we can finally move on to practice and consider what to use. But more about that in the following articles.
Part 2
In this part we will make a small digression from digital signatures in the direction of that, without which directly digital signatures, and even the protection of information in the usual sense, would not be: encryption. After all, the first thing that comes to mind when it comes to protecting our data is not to give this data to a bad person to read. Therefore, before continuing to examine the standards of PGP and S / MIME, it is worth painting out some white spots that remain in knowledge, and consider the encryption process in a bit more detail.
Ciphers and codes exist, probably, from the moment humanity learned to record their impressions of the world around us on media. If you think about it a little, even an ordinary alphabet is already a cipher. After all, when we read a text, in our head a certain sound, a combination of sounds, or even a whole concept is compared to each character, and this does not happen in the head of a neighbor who does not know how to read.
')
Without knowing which symbol and what is matched, we can never understand what exactly the writer had in mind. For example, try to take and read something written in Hebrew or in Chinese. The alphabets of these languages themselves will be an insurmountable obstacle for you, even if the concepts of your native language are written with the help of these symbols.
But, nevertheless, the mere use of someone else's alphabet is still insufficient measure to protect your data. After all, any alphabet, anyway, was created for ease of use and is inextricably linked with the language to which this alphabet is characteristic. So, having learned this language and some set of basic concepts on it (or even just using the services of a person who knows the given language), a bad person can read your information.
So, we need to come up with an alphabet that knows only a limited circle of people, and use it to record information. Surely everyone read (or at least heard) a cycle of stories about Sherlock Holmes. This cycle featured an alphabet made up of dancing little men (and many, I think, made up their own based on it in childhood). However, as this story shows, an observant person can figure out which symbol belongs to what. So our information will again fall into the wrong hands.
What to do? Come up with more and more complex alphabets? But the more complex and cumbersome the alphabet, the more inconvenient it is to work with it, to keep it secret. In addition, there is a wonderful proverb about mystery: two people know - everyone knows. After all, the weakest link in any cipher is a person who knows how to decrypt this cipher.
And why not make it so that the encryption method is immediately known to everyone, but it would be impossible to decrypt our data without some kind of key? After all, the key (unlike the entire alphabet) is small, it is easy enough to make a new one, if that (again, unlike the processing of the entire alphabet), it is easy to hide. The most vividly the advantages of key systems are shown by the following example: the recipient needs to read the message you sent. Plain, on paper. Let's say you use a secret alphabet. Then, in order to read the message, the recipient must know the alphabet, have a large dusty Talmud, which describes how to decrypt (after all, the alphabet must be complicated to be reliable) and understand how to work with this Talmud. With keys, everything is simpler: you put the message in a box with a lock, and the recipient simply inserts a suitable key, and you need to know how the lock works.
So, the well-known "alphabets" and keys - a mechanism that is much more convenient than just alphabets. But how to encrypt so that everything is decrypted with a simple key? And this is where mathematics comes to the rescue, and more specifically, mathematical functions that can be used to replace our original symbols with new ones.
Recall what a function is. This is some relation by which from one number you can get another. Knowing x and substituting it into the known relation y = A * x, we always get the value of y. But, as a rule, the opposite is also true: knowing y, we can also get x.
As a rule, but not always. For many dependencies, getting y is easy, whereas x is already very difficult, and getting it will take a long time. It is precisely on such dependencies that the encryption used now is based.
But back to encryption itself. Encryption is divided into symmetric , asymmetric, and combined . Consider the essence of each of them.
Symmetric encryption , by and large, is quite slightly different from the good old secret alphabet. As a matter of fact, it differs just in the presence of a key - some relatively small sequence of numbers, which is used for encryption and decryption. At the same time, each of the parties exchanging information should know this key and keep it secret. A huge advantage of this approach is the encryption speed: the key, in fact, is a fairly simple and short instruction, which symbol, when, and with which to replace. And this key works in both directions (that is, with it you can both replace all the characters with new ones, and return everything as it was), for which this encryption method was called symmetric. Equally a huge disadvantage is the fact that both parties, between which information is sent, must know the key. At the same time, it is worth it for a bad person to get the key, as he immediately reads our carefully protected data, which means the problem of handing over the key to the receiving party becomes full length.
Asymmetric encryption comes a little trickier. Here both we and our recipient already have two keys that are called open and closed. We also keep the recipient's private key (note that everyone only keeps his own key, which means we’re already going beyond the very same proverb about the two who know), and we can safely transfer the public key to anyone — our private, secret, it can not be restored. Total, we use the recipient's public key for encryption, and the recipient, in turn, uses his private key to decrypt. The advantage of this approach is obvious: we can easily start sharing secret information with different recipients, practically nothing (assuming that our recipient did not lose / give away his private key, etc., that is, did not transfer it into the hands of a bad person) when transmitting information. But, without a huge minus is not enough. And here it is as follows: in this case, encryption and decryption go very, very, very slowly, two or three orders of magnitude slower than similar operations with symmetric encryption. In addition, resources for this encryption is also spent much more. And the keys themselves for these operations are significantly longer than those for symmetric encryption operations, since it is necessary to secure the private key as much as possible from matching the public key. So, it is simply unprofitable to encrypt large amounts of information in this way.

An example of using asymmetric encryption [Wikipedia]
e - recipient's public key B
d - recipient's private key B
m - the source information of the sender A
c - encrypted source information
And again the question arises: what to do? And you need to do the following: take and combine both methods. Actually, this is how we get the combined encryption. We will encrypt our large amount of data using the first method, and in order to convey the key with which we encrypted them to the recipient, we will encrypt the key using the second method. Then we get that even though asymmetric encryption is slow, the volume of encrypted data (that is, the key on which large data is encrypted) will be small, which means that decryption will pass fairly quickly, and more rapid symmetric encryption will come in later.

An example of the use of the combined system [Wikipedia]
All these mechanisms have been applied in practice, and both of our large camps PGP and S / MIME use them. As stated in the first article, asymmetric encryption is used to digitally sign (that is, to encrypt our hash). The difference of this application from the usual asymmetric encryption is that our private key is used for encryption, and for decryption, the presence of the public key associated with it is sufficient. Since we don’t hide the public key, our hash can be read by anyone, not just the individual recipient, which is required for a digital signature.
Combined encryption is used in both standards directly to encrypt the data sent.
Thus, starting to use digital signatures to protect our data from being tampered with, we automatically (for these two standards) also get a wonderful opportunity to protect our data from reading as well, which you will agree is very convenient.
Now that we have become familiar with the general principles of the mechanisms used to protect our data, we can finally move on to practice and consider what to use. But more about that in the following articles.
Source: https://habr.com/ru/post/98323/
All Articles