H #, create your programming language

Good day.
In this article I want to review one of the main innovations in Visual Studio 2010, namely, the functional programming language F #.

We will consider the syntax and potential of F # using the example of creating our own interpreter for the programming language invented by us (After all, it is always more interesting to talk about something with examples).

We describe the task that we are going to solve, namely the syntax of our programming language, it will be quite simple, here’s something that we want to see:

function Summ(a,b,c)
{
val d = a+b+c;
print d;
return d;
}

function MyEvaluations(a,b,c)
{
val in = Summ(a,b,1);
val out = Summ(b,c,1);
val d = in*out;
return d;
}

function Program()
{
print(MyEvaluations(1,2,3));
}


So, we have support for functions with parameter passing and return value, printing, arithmetic operations, and local variables.
We will start to implement it, for this we need to install the additional package F # Power Pack from here

Vocabulary

Now we create a new F # project from the online F # Parsed Language Starter template and clear all files except lexer.fsl
In order to deal with the contents of this file, let's first analyze our language by bone. Under the word "lexeme", we will understand the minimum building blocks of which a programming language consists.
The lexemes include keywords, brackets, commas, names, in general, everything that the source code of the program consists of. At the level of tokens, we do not have functions and other logical units.
')
Open the lexer.fsl file
In F #, the analogue of the namespace is the module keyword, the using analogue is the open keyword, so the first thing we will write now is the definition of the area in which we work:

{
module Lexer
open System
open Parser
open Microsoft.FSharp.Text.Lexing

let lexeme lexbuf =
LexBuffer<char>.LexemeString lexbuf
}
let digit = [ '0' - '9' ]
let whitespace = [ ' ' '\t' ]
let newline = ( '\n' | '\r' '\n' )
let symbol = [ 'a' - 'z''A' - 'Z' ]

Variables in F # are declared using the let keyword, also, we can use regular expressions here.
So, delete all the code below the line.

rule tokenize = parse

which is a service marker, denoting that the description of our language goes below, and insert the following code:

| whitespace { tokenize lexbuf }
| newline { tokenize lexbuf }

// Operators
| "+" { PLUS }
| "-" { MINUS }
| "*" { MULTIPLE }
| "/" { DIVIDE }
| "=" { EQUALS }

// Misc
| "(" { LPAREN }
| ")" { RPAREN }
| "," { COMMA }
| ";" { ENDOFLINE }
| "{" { BEGIN }
| "}" { END }

// Keywords
| "function" { FUNCTIONKW }
| "return" { RETURN }
| "var" { VARIABLE }


Since this file will be processed by additional means of the PowerPack library, the F # code in this file is immediately surrounded by the first block of curly braces.
This is the simplest part, here we simply write string constants or regular expressions that are present in our language, we will have a few of them: arithmetic operators, brackets, three keywords, a comma and a semicolon.
Further, using regular expressions, we will teach our interpreter to “pull out” the numbers and the names of variables / functions from the code. In fact, at this stage we turned our plain text code into such a sequence of objects:

FUNCTIONKEYWORD NAME LPAREN NAME COMMA NAME COMMA NAME RPAREN
BEGIN
VARIABLE NAME EQUALS NAME PLUS NAME PLUS NAME ENDOFLINE
…..


Each object has its own type, which is specified in the example above.
However, the DECIMAL and NAME objects must also have a value.
To do this, we write the following lines:

| digit+( '.' digit+)? { DECIMAL(Double.Parse(lexeme lexbuf)) }
| symbol+ { VARNAME(String.Copy(lexeme lexbuf)) }

| eof { EOF }

It can be interpreted as a constructor call. All that is in curly brackets is our data types. After processing, the program text will be a sequence of objects of these types.
eof - service lexeme, signaling the end of parsed text

Syntax parsing

To make it a little clearer where data types come from, and why NAME has string content, and DECIMAL is numeric - open the Parser.fsy file and paste the following code into it:

%{
open ParserLibrary
open System
%}

%start start

%token <Double> DECIMAL
%token PLUS MINUS MULTIPLE DIVIDE
%token LPAREN RPAREN
%token FUNCTIONKW RETURN VARIABLE
%token BEGIN END
%token EQUALS
%token <String> VARNAME
%token ENDOFLINE
%token COMMA
%token EOF
%type <WholeProgram> start

%%


All our data types are listed here, if our type must have a value, then the type of this value is written in angle brackets.
start is the so-called “grammar axiom”, something that we will try to “assemble” when interpreting our code.

A grammar is written in the following form:

: | | | … | …

The first line will look like this:

start: | WholeProgram

This suggests that the purpose of our analysis is to get "the whole program"
"The whole program" in the closer look we have is just a list of functions
Therefore, we write this fact:

WholeProgram:
| FunctionDescription
| WholeProgram FunctionDescription

It is worth noting a rather unusual type of formation of lists in this form of record, the fact is that the number of “components” for each element must be fixed, and in order not to limit the number of possible functions in our language, we go to this trick. When the system finds the first function - it creates a WholeProgram object from it, when it sees the second function - we have the WholeProgram (from the first function) and FunctionDescription (the second function) next to us, and the system collapses both of these objects into a new WholeProgram, thus removing the restriction on the total number of functions in the program text.
If we illustrate the grammar, we will get something like the following image:

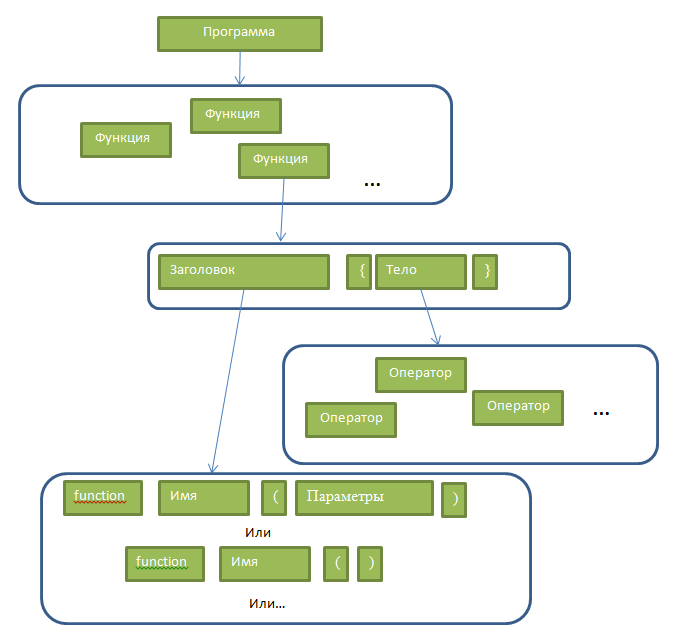
We now write what the function is:

FunctionDescription:
| FunctionKeyWord FunctionTitle Begin End
| FunctionKeyWord FunctionTitle Begin OperatorsList End

We could confine ourselves to the second variant of the presentation, but in this case empty functions would lead to an error in the interpreter, as can be seen from the code, the function consists of a keyword, a title, curly brackets and, possibly, a set of statements inside the function - its body.
The function header consists of its name, parentheses and, possibly, a list of parameters:

FunctionTitle:
| VarName LParen RParen //
| VarName LParen VarName RParen // . ,
| VarName LParen VarName AdditionParametersList RParen //

The AdditionParametersList and OperatorsList objects are lists and therefore are defined in the same way as the WholeProgram:

OperatorsList:
| Operator
| OperatorsList Operator

AdditionParametersList:
| Comma VarName
| AdditionParametersList Comma VarName

The operator is one line of our program inside the function body, let there be two options in our language:

Operator:
| VaribaleKeyWord VarName Equals Expression EndOfLine
| ReturnKeyWord Expression EndOfLine

For example, what corresponds to the lines:

val d = in*out;
return d;

Initially, we had 4 arithmetic operations defined, we take into account that multiplication and division are higher-priority operations than addition and subtraction:

Expression:
| Expression PLUS HighExpression
| Expression MINUS HighExpression
| HighExpression // "Operator"' Expresson, "" .
HighExpression:
| HighExpression MULTIPLY Operand
| HighExpression DIVIDE Operand
| Operand // , - .

This separation allows you to parse the expression 2 + 2 * 2 as Expression Plus HighExpression, and then expand HighExpression into a separate subtree: Expression Plus (HighExpression MULTIPLY Operand), which will allow you to correctly process the priority of operations.
At the lower level, with an operand, we can have either a number, the name of an existing variable, the name of a function, or (if we want) an expression in brackets.

Operand:
| DECIMAL
| VarName
| FunctionTitle
| LParen Expression RParen // Expression , .

Let's return to our F # (now in its pure form) and consider this possibility as constructors with pattern matching, namely, we will describe the data types we just used

namespace ParserLibrary
open System

type Operator =
| VarOperator of string * Expression
| ReturnOperator of Expression

and Operand =
| DECIMALOP of Double
| SUBEXPROP of Expression
| VARNAMEOP of String
| FUNCOP of FunctionTitle

and HighExpression =
| MULTIPLY of HighExpression * Operand
| DIVIDEOP of HighExpression * Operand
| VAR of Operand

and Expression =
| SUMM of Expression * HighExpression
| SUB of Expression * HighExpression
| HighExpression of HighExpression

and FunctionTitle = String * List<String>
and FunctionDescription = FunctionTitle * OperatorsList
and OperatorsList = List<Operator>
and AdditionParamsList = List<String>
and WholeProgram = List<FunctionDescription>

In fact, we declared 9 objects, each of which has several named constructors with different parameters (in fact, such a set of constructors is similar to a union in C ++)
Note that the asterisk "*" in this context is not a multiplication, but a parameter separator, i.e. a constructor with the name VarOperator for the Operator type accepts a string (string) and an expression (expression)
All that remains to be done to complete the first part of the writing of our interpreter is to link these data types in the Parser.fsy file; for this, we write the corresponding constructor in front of each condition in curly braces.
It will look like this:

start: WholeProgram { $1 }

WholeProgram:
| FunctionDescription { $1 :: [] }
| WholeProgram FunctionDescription { $1 @ ($2 :: []) }

FunctionTitle:
| VARNAME LPAREN RPAREN { $1, [] }
| VARNAME LPAREN VARNAME RPAREN { $1, $3 :: [] }
| VARNAME LPAREN VARNAME AdditionParamsList RPAREN { $1, $3 :: $4 }

AdditionParamsList:
| COMMA VARNAME { $2 :: [] }
| AdditionParamsList COMMA VARNAME { $1 @ ($3 :: []) }

OperatorsList:
| Operator { $1 :: [] }
| OperatorsList Operator { $1 @ ($2 :: []) }

FunctionDescription:
| FUNCTIONKW FunctionTitle BEGIN END { $2, [] }
| FUNCTIONKW FunctionTitle BEGIN OperatorsList END { $2, $4 }

Operator:
| VARIABLE VARNAME EQUALS Expression ENDOFLINE { VarOperator($2, $4) }
| RETURN Expression ENDOFLINE { ReturnOperator($2) }

Expression:
| Expression PLUS HighExpression { SUMM($1, $3) }
| Expression MINUS HighExpression { SUB($1, $3) }
| HighExpression { HighExpression $1 }

HighExpression:
| HighExpression MULTIPLE Operand { MULTIPLY($1, $3) }
| HighExpression DIVIDE Operand { DIVIDEOP($1, $3) }
| Operand { VAR $1 }

Operand:
| DECIMAL { DECIMALOP($1) }
| VARNAME { VARNAMEOP($1) }
| FunctionTitle { FUNCOP($1) }
| LPAREN Expression RPAREN { SUBEXPROP($2) }

$ 1, $ 2, etc. Is the number of the variable in the condition
Using this code as an example, let's take a look at another great feature of F # - working with lists.
The expression A :: B means creating and returning a new list based on the list B with the addition of the element A
[] - empty list
We can also set lists in code directly or from ranges, for example:
[1,2,3,4,5] or [1..5]
In this case, 100 :: [1..5] will return this list to us: [100,1,2,3,4,5]
The @ operator is the creation of a new list from the union of two existing ones.
For example: [1..5] @ [6..10] returns [1..10]

Note that in the case of a choice by template - we specify a named constructor, for the same types that are simply synonymous with any tuples (FunctionDescription, OperatorsList, etc.) - we simply list the parameters in the order we declared in tuple.
So, this is all that is necessary for us to make a parse tree from simple F # text, the second part is interpretation.
Open the Program.fs file and write open for the namespaces that we will use:

open System
open Microsoft.FSharp.Text.Lexing
open System.Collections.Generic;
open ParserLibrary
open Lexer
open Parser


Interpretation

Further, for interpretation, we will need to have a list of functions (or better, a dictionary), named stacks for each function (so that there are no conflicts of variable names) and the name of the function currently being executed.
To do this, we declare variables using the let keyword we already know:

let stack = Dictionary<String, Dictionary<String,Double>>()
let functionsList = Dictionary<String, FunctionDescription>()
let mutable currentFunctionName = "Program" ;


In classical functional programming, all objects are immutable, this can be seen in the example of working with lists, when instead of adding an element to the list, we create a new one based on existing ones. This allows you to safely parallelize the program, because no need to have complex synchronization to write.
F #, being a functional language, perfectly supports the entire .NET library, allowing you to work with mutable objects. Full copying of data in this case does not occur, only references to objects are copied, this allows you to reach a compromise on speed without breaking the ability to parallelize data beautifully, a kind of copy on write if you want.

So, let's interpret:
Start by parsing the expression.
We declare a function with a choice by template, let rec are keywords, EvaluateExpression is a name, expression is a parameter.
Recall that by declaring types we created constructors with a choice on a template, we use the same templates when choosing a branch for executing a function. For example: if the passed expression parameter was created using the SUMM constructor (expression, highExpression), then we perform the branch of addition, etc.
It can be noted that this function almost repeats the constructors created earlier, assigning to each of them a specific action.

let rec evaluateExpression expression =
match expression with
| SUMM (expr, hexpr) -> (evaluateExpression expr) + (evaluateHighExpression hexpr)
| SUB (expr, hexpr) -> (evaluateExpression expr) - (evaluateHighExpression hexpr)
| HighExpression hexpr -> evaluateHighExpression hexpr

and evaluateHighExpression highExpression =
match highExpression with
| MULTIPLY (hexpr, oper) -> (evaluateHighExpression hexpr) * (EvaluateOperand oper)
| DIVIDEOP (hexpr, oper) -> (evaluateHighExpression hexpr) / (EvaluateOperand oper)
| VAR oper -> EvaluateOperand oper

and EvaluateOperand oper =
match oper with
| DECIMALOP x -> x
| VARNAMEOP x -> stack.Item(currentFunctionName).Item(x)
| FUNCOP x -> evaluateFunction x
| SUBEXPROP x -> evaluateExpression x

Since we have introduced support for variables and functions, we need to write handlers for this case. In the case of variables, everything is more or less simple, we go to a dictionary containing the values ​​of the variables of the current function and get the value by the name of the variable (remember that VARNAMEOP is associated with the String type)

In the case of hitting a function, we need to copy the parameters from the calling function in accordance with the function header and start its execution.
To do this, we add the following code:

and evaluateFunction(f:FunctionTitle) =
let caller = currentFunctionName;
let newStack = Dictionary<String, Double>()
let realParams = functionsList.Item (f |> GetFunctionName) |> GetFormalParamsListDecription

let formalParams = GetFormalParamsListTitle(f)
ignore <| List.mapi2 ( fun i x y -> newStack.Add(x, stack.Item(caller).Item(y))) realParams formalParams

currentFunctionName <- GetFunctionName(f)
stack.Add(currentFunctionName, newStack)

let operatorsList = functionsList.Item(GetFunctionName f) |> GetOperatorsList

let result = RunFunction operatorsList

ignore <| stack.Remove(currentFunctionName)

currentFunctionName <- caller
result
//

This is also a function, but no longer with a choice on the basis of a template, but in a more familiar form.

Let's sort the operator of the pipeline (pipeline) “|>”, in fact, it is a more understandable way to call chains of functions, if earlier we had to write OuterFunction (InnerFunction (Validate (data))), then in F # you can “expand” this chain: data |> Validate |> InnerFunction |> OuterFunction
Both entries lead to the same result, but when using the “|>” operator, we use functions from left to right, in the case of long chains, this is more convenient.
A feature of these functions is that we do not need to write return, for example, the function
test (a) = a * 10
returns a * 10, this is partly convenient, but we need to take care not to return any value "by chance" (by the way, VS will emphasize all unintended returns), for this we use the ignore method, which does nothing and nothing returns that we have all ignore at the beginning of the line - we use the inverse pipelined operator "<|", it does the same as “|>”, only in the opposite direction, now the functions are applied from right to left.
In the case of simple assignment, to avoid returning the value, instead of “=”, the “<-“ operator is used.

Let's analyze the line in more detail:

ignore <| List.mapi2 ( fun i x y -> newStack.Add(x, stack.Item(caller).Item(y))) realParams formalParams

The List class contains a set of mapi * methods (for different numbers of lists), the essence of these methods is that they process several lists (in our case 2) in parallel, passing the element number in both lists and the elements themselves to the handler function, assuming that they are lists are equal. The mapi2 method takes 3 parameters, a handler function and two lists to be processed.
For example, as a result of executing the following code:

let firstList = [1..5]
let secondList = [6..10]
ignore <| List.mapi2 ( fun i x y -> Console.WriteLine(10*x+y)) firstList secondList

We will get the result: 16 27 38 49 60

Since the order of the parameters in brackets when calling a function and when describing it in our language is the same, we simply process the elements from the lists of the call and the function declaration in pairs.
The fun keyword defines a new function (you can draw an analogy with lambdas in C #), which we will use to process lists, our function takes 3 parameters, i is the number of the current element in both lists, x and y are the elements from the first and second lists respectively .
So here we are copying to our new stack a variable from the stack of the calling function.

After preparing the parameters, we call the function, memorize the result, delete the dictionary (stack), and restore the name of the calling function.

let result = RunFunction operatorsList

ignore <| stack.Remove(currentFunctionName)

currentFunctionName <- caller
result

Because no need to write return, to return the value, just write the name of the variable that we want to return.

Now we write the runFunction method:

and RunFunction(o:OperatorsList) =
ignore <| List.map ( fun x -> EvaluateOperator x) o
stack.Item(currentFunctionName).Item( "return" )

The List.map method iterates over all elements of the list, then we simply return the resulting variable from our current stack.

and EvaluateOperator operator =
match operator with
| VarOperator (name, expr) -> stack.Item(currentFunctionName).Add(name, evaluateExpression expr)
| ReturnOperator expr -> stack.Item(currentFunctionName).Add( "return" , evaluateExpression expr)

In our language, there are only 2 types of operators, this is either a declaration of a variable or a return value, in both cases we calculate the value and add it to the dictionary (stack), in the case of return we use the fact that return in our language is a key word and we can safely use it for their own purposes, without fear of conflict with an already declared variable.
Since we want to use a couple of predefined functions in our language, for I / O, we add a few checks:

and RunFunction(o:OperatorsList) =
if currentFunctionName.Equals "print" then
stack.Item(currentFunctionName).Add( "return" , 0.0)
Console.WriteLine(stack.Item(currentFunctionName).Item( "toPrint" ).ToString())
if currentFunctionName.Equals "get" then
Console.Write( "Input: " );
stack.Item(currentFunctionName).Add( "return" , Double.Parse(Console.ReadLine()))
if currentFunctionName.Equals "Program" then
stack.Item(currentFunctionName).Add( "return" , 1.0)

ignore <| List.map ( fun x -> EvaluateOperator x) o
stack.Item(currentFunctionName).Item( "return" )

We check the name of the function and, depending on the result, execute or print the value of the variable, or read the value from the keyboard.
In order not to write in the main method return - we define the spec. variable before the execution of the function body.

F # uses meaningful padding, in particular, to select the body of if blocks.
The last thing left to do is to identify the missing functions that we used and write a shell that our parser will use:

let GetFunctionName f = match f with name, foo -> name
let GetFunctionNameDescription f = match f with t, foo -> GetFunctionName t
let GetFormalParamsListTitle t = match t with foo, paramerers -> paramerers
let GetFormalParamsListDecription f = match f with t, foo -> GetFormalParamsListTitle t
let GetOperatorsList f = match f with foo, o -> o
let GetTitle f = match f with t, too -> t

Since we declared some types simply synonyms, after the word with does not come the name of the constructor, there is just an enumeration of all parameters, after the arrow comes the body of the function, in this case we just write the name of the variable to be returned.
If writing a function call without parentheses is unusual for you, F # allows you to write code like this:

let GetFunctionName(f) = match f with name, foo -> name
let GetFunctionNameDescription(f) = match f with t, foo -> GetFunctionName(t)
let GetFormalParamsListTitle(t) = match t with foo, paramerers -> paramerers
let GetFormalParamsListDecription(f) = match f with t, foo -> GetFormalParamsListTitle(t)
let GetOperatorsList(f) = match f with foo, o -> o
let GetTitle(f) = match f with t, too -> t

These entries are absolutely equivalent.

Finishing touches

And finally the last:

printfn "H#"

let mutable source = "" ;
let rec readAndProcess() =
printf ":"
match Console.ReadLine() with
| "quit" -> ()
| "GO" ->
try
printfn "Lexing..."
let lexbuff = LexBuffer<char>.FromString(source)

printfn "Parsing..."
let program = Parser.start Lexer.tokenize lexbuff
ignore <| List.map ( fun x -> functionsList.Add(GetFunctionNameDescription(x),x)) program
functionsList.Add( "print" ,(( "print" , [ "toPrint" ]), []))
functionsList.Add( "get" ,(( "get" , []), []))
printfn "Running..."
ignore <| (functionsList.Item( "Program" ) |> GetTitle |> evaluateFunction)

with ex ->
printfn "Unhandled Exception: %s" ex.Message

readAndProcess()
| expr ->
source <- source + expr
readAndProcess()

readAndProcess()

We define a new function in which we will try to parse the string entered from the keyboard, if the parsing is completed successfully, we add all the functions from the resulting list (program) to our variable functionsList.
To call a function at the beginning of the program, simply write its name without indents at the end of the file.
Since we have two predefined functions in our language (get and print), we add them, then we perform a function with the name Program.

The last thing that can be described in this example is an interesting way to construct objects for which we have not defined constructors through match.

and FunctionTitle = String * List<String>
and FunctionDescription = FunctionTitle * OperatorsList
and OperatorsList = List<Operator>
and AdditionParamsList = List<String>
and WholeProgram = List<FunctionDescription>

If we expect the FunctionTitle object, to create it, it is enough to enclose its parameters (String and <ListString>) in parentheses, there is no need to specify the data type.

( "print" ,(( "print" , [ "toPrint" ]), []))

Launch

Well, let's run our interpreter: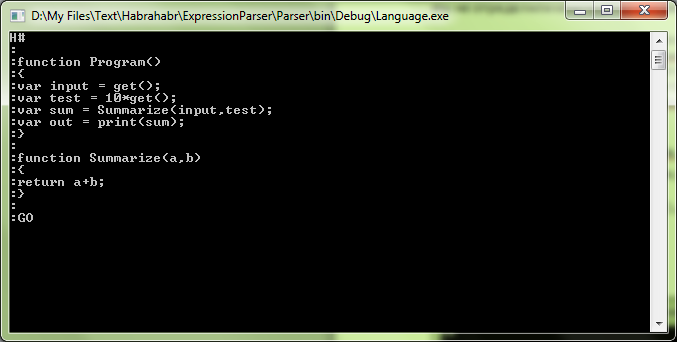


After pressing Enter we will see an invitation to enter the value of the variable:


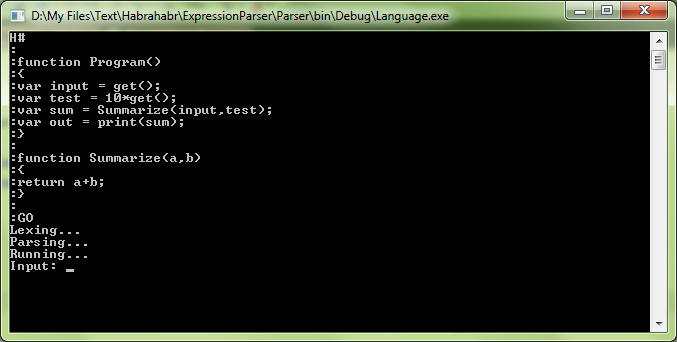
And after that:


Well, the program really works.
The source code with binaries can be downloaded here .

If you now look at the F # code once more, you can see that we wrote a minimum, just describing what we want to do, it allowed us to write our own interpreter and fit only ~ 200 lines of code, F # allows us to get rid of the routine writing work code that does not answer the question “what”, but answers the question “how”. Of course, programming in this language seems difficult at first, but in some cases it is worth it, as it allows you to write flexible code that is easy to maintain.
Thanks for attention.