10 unnatural ways to calculate Fibonacci numbers
The task of calculating the first two dozen Fibonacci numbers has long lost practical value for programmers and is used primarily to illustrate the basic principles of programming — recursion and iteration. I use it to demonstrate several programming languages in which it acquires an unusual and sometimes even unhealthy look.
So, my rating of the ten most unnatural ways to calculate the Fibonacci numbers I have written over the past six months in the framework of the Progopedia project. To clarify the problem, we require that the output of the program be the first 16 numbers in the form
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...
A visual programming language in which all elements of the language are represented as elementary blocks from which the “code” itself is composed, called the flow diagram. This language has earned a place in the ranking by the size of diagrams (two, well three dozen elements - the maximum that can be used on one diagram without scrolling and final entanglement in the links between the blocks) and the inconvenience of using key structures of the language (each cycle or conditional transition requires one or several individual diagrams that instantly clutter up the program logic with multi-level nesting and transfer of global variables as loop parameters). Well, in fact, visuality - the program is not written, but drawn, and the keyboard as such is used only for entering values of constants and (optionally) renaming elementary blocks and writing comments.
')

Main flow chart

Cycle body
The peculiarity of this language (up to version 4.4.0) is the absence of cycles as such. However, this can be forgiven - after all, gnuplot is not a general-purpose language, but a program for plotting graphs. A cycle can be simulated by creating a separate interpretable file with the body of the cycle, which is “read” to start the cycle and “reread” for each iteration.
Run.gp file (main)
File fibonacci.gp (imitation cycle)
Lazy calculations complete with endless lists - one of the most famous Haskell chips - allow you to determine (but not calculate) the Fibonacci numbers in one line of code, the rest of the code requests the right numbers and displays them in the right format. Still, for a programmer who has received a classic education within the procedural paradigm, this method is far from obvious and certainly not natural.
Of course, SQL itself is not a programming language, and in most implementations a procedural extension is attached to it, using which the problem is solved in a completely classical way. Of interest is the solution without extensions, on "pure" SQL. However, it will not be possible to solve on “pure” SQL - according to the standard, the query language does not contain anything that could be used as a loop. Solutions are obtained dependent on the specific implementation and the accompanying buns.
In the internal query, indices of numbers are generated (from 1 to 16) using the level pseudo-column and the connect by construct. In the following query, the Fibonacci numbers themselves are calculated from their indices using the Binet formula. The remaining two queries order the numbers by their indices and combine them into one line of the desired format.
A convenient, but rarely used and therefore little-known model operator allows you to implement a loop within an SQL query.
The ability to calculate query results in a loop is implemented more succinctly than in Oracle.
Another rather concise implementation of loops, this time with a recursive query.
FP is a prototype of all existing programming languages that use the programming-level programming paradigm (function-level, not to be confused with functional, that is, simply functional ). Invented in 1977, it is more a mathematical model than a real programming language: it did not even have an official standard (except for the only article in which it is described), not to mention the implementation! However, in our time there are interpreters of this language, usually written in the framework of student work. One of them is Furry Paws , and its cozy name does not at all correspond to the "comfort" of its use.
Programming at the function level involves building a program from elementary functions that can be combined using functionals (functional forms). So, ~ 1 is an elementary function that always returns the value 1; id is a function that returns the value passed to it, [] is a functional form that combines its arguments into a sequence, etc.
Another language that uses “function-level programming” is a worthy successor to FP. Interestingly, almost any expression on it can be written in several ways, from almost traditional to completely unnatural (as required in this article). So, for example, calculating Fibonacci numbers using the Binet formula can be written quite civilized:
And you can replace almost all mathematical operations with their equivalents specific to J:
And it will hardly be obvious to anyone that%: - is the extraction of the square root,>: - increment, -: - division by two, and% ~ - division, and when writing, the dividend and divisor are swapped.
Calculation using recursion:
A little-known esoteric language, interesting for its minimalism and the use of a stack-based memory model. Unlike the following language, the main difficulty lies not in performing arithmetic operations, but in obtaining the contents of precisely those stack elements that are needed at each step. Printing, however, is also unpleasant, so only the first six numbers are calculated and displayed.
Language descriptions and comments on the given code can be found on the Hanoi Love page.
Classic esoteric programming genre - Brainfuck. A language in which even copying or addition is not an elementary operation, printing
a three-digit number is worthy of a separate ode, and using it to solve a specific task is a masochist’s dream: well ;-)
In the authoring interpreter (Muller's Brainfuck) the contents of memory cells are stored in variables of type byte, and the Fibonacci numbers from the 14th to the 16th would cause an overflow of memory. The implementation of long arithmetic on Brainfuck is no longer a symptom, but practically a diagnosis, therefore, when writing a solution, it was assumed that the memory cell can store numbers up to 1000 (in many implementations of the language, quite capacious data types are used for storage).
Language descriptions and comments on the code can be found on the Brainfuck page.
The simplest of the graphic dialects of Brainfuck, invented by Lode Vandevenne.
Programs are read from PNG pictures, commands are written in pixels of different colors, and eight more commands are added to eight commands in Brainfuck - control of the pointer to the current pixel. To all the delights of Brainfuck, the complete unreadability of the “code” and the complete impossibility are added.
“Encode” without ancillary tools (for example, a converter of programs and pictures).
The author's interpreter of the language has sunk into oblivion, so for the generation of the “program” I had to write my own. The “program” is shown in a tenfold increase.
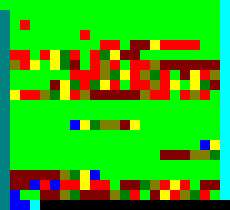
Where is worse? - the reader will think, flipping through the screen with a quivering hand Yes, it gets worse. In previous languages, the program could at least embrace the eye, and this is already a lot.
Meet the winner of the rating - Unary. The Brainfuck dialect, invented by the same Lode Vandevenne (oh, Monsieur knows a lot about perversions!), Assumes that Brainfuck commands are converted into binary codes and concatenated into one binary number, the unary record of which is a program on Unary. The program for generating Fibonacci numbers is a string of
167967665105731198557055496639385943332278803897935697536099438828197
665241403160165880863622431582784595268769268183940269756210147305655
704025762911607244068691728105306566342622386432823429136972542304655
647901781271798433263001837026612851345264031562174039657802748245705
398528237993320520942720239597540583536934220029626573406470088757427
393143000966310611249037587993216365993804186165097620168960460854977
571944373603975793034586829061577464233522714007498991416860375267535
193648636795096472789203729505034887001634966681420589637468649908257
407260923590831776308356684326657774592110098643361324426156431864437
942781495979555960608253552679248495326880775320385281559763269974848
026839024530519989287202261977272377723622502479809174132505837648641
033569945906182518892142219706483917757108086522763280388915772444727
238483811923456440363260610571471034139736312976255142288379411989404
9017738035 (that is, approximately 1.68 * 10 ^ 906) zeros.
I am sure that the languages listed here are far from the worst thing a programmer may encounter (in any case, not all of them :-)), but I'm not a magician, I'm just learning.
So, my rating of the ten most unnatural ways to calculate the Fibonacci numbers I have written over the past six months in the framework of the Progopedia project. To clarify the problem, we require that the output of the program be the first 16 numbers in the form
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...
10. Sanscript
A visual programming language in which all elements of the language are represented as elementary blocks from which the “code” itself is composed, called the flow diagram. This language has earned a place in the ranking by the size of diagrams (two, well three dozen elements - the maximum that can be used on one diagram without scrolling and final entanglement in the links between the blocks) and the inconvenience of using key structures of the language (each cycle or conditional transition requires one or several individual diagrams that instantly clutter up the program logic with multi-level nesting and transfer of global variables as loop parameters). Well, in fact, visuality - the program is not written, but drawn, and the keyboard as such is used only for entering values of constants and (optionally) renaming elementary blocks and writing comments.
')

Main flow chart

Cycle body
9. gnuplot
The peculiarity of this language (up to version 4.4.0) is the absence of cycles as such. However, this can be forgiven - after all, gnuplot is not a general-purpose language, but a program for plotting graphs. A cycle can be simulated by creating a separate interpretable file with the body of the cycle, which is “read” to start the cycle and “reread” for each iteration.
Run.gp file (main)
#!/usr/bin/env gnuplot
i = 1
a = 1
b = 1
res = ''
load "fibonacci.gp"
print res, '...'File fibonacci.gp (imitation cycle)
res = res . a . ', '
c = a
a = b
b = b+c
i = i+1
if (i <= 16) reread8. Haskell
Lazy calculations complete with endless lists - one of the most famous Haskell chips - allow you to determine (but not calculate) the Fibonacci numbers in one line of code, the rest of the code requests the right numbers and displays them in the right format. Still, for a programmer who has received a classic education within the procedural paradigm, this method is far from obvious and certainly not natural.
module Main where
import Text.Printf
fibs :: [Int]
fibs = 0 : 1 : zipWith (+) fibs (tail fibs)
line n = printf "%d, " $ fibs !! n
main = do
sequence_ $ map line [1..16]
putStrLn "..."7. SQL
Of course, SQL itself is not a programming language, and in most implementations a procedural extension is attached to it, using which the problem is solved in a completely classical way. Of interest is the solution without extensions, on "pure" SQL. However, it will not be possible to solve on “pure” SQL - according to the standard, the query language does not contain anything that could be used as a loop. Solutions are obtained dependent on the specific implementation and the accompanying buns.
7.1. Oracle SQL (since version 9i)
In the internal query, indices of numbers are generated (from 1 to 16) using the level pseudo-column and the connect by construct. In the following query, the Fibonacci numbers themselves are calculated from their indices using the Binet formula. The remaining two queries order the numbers by their indices and combine them into one line of the desired format.
SELECT REPLACE(MAX(SYS_CONNECT_BY_PATH(fib||', ', '/')),'/','')||'...' FROM ( SELECT n, fib, ROW_NUMBER() OVER (ORDER BY n) r FROM (select n, round((power((1+sqrt(5))*0.5, n) -power((1-sqrt(5))*0.5, n))/sqrt(5)) fib from (select level n from dual connect by level <= 16) t1) t2 ) START WITH r=1 CONNECT BY PRIOR r = r-1; 7.2. Oracle SQL (from version 10g)
A convenient, but rarely used and therefore little-known model operator allows you to implement a loop within an SQL query.
select max(s) || ', ...' from (select s from dual model return all rows dimension by ( 0 d ) measures ( cast(' ' as varchar2(200)) s, 0 f) rules iterate (16) ( f[iteration_number] = decode(iteration_number, 0, 1, 1, 1, f[iteration_number-1] + f[iteration_number-2]), s[iteration_number] = decode(iteration_number, 0, to_char(f[iteration_number]), s[iteration_number-1] || ', ' || to_char(f[iteration_number])) ) ); 7.3. Mysql
The ability to calculate query results in a loop is implemented more succinctly than in Oracle.
select concat(group_concat(f separator ', '), ', ...') from (select @f := @i + @j as f, @i := @j, @j := @f from information_schema.tables, (select @i := 1, @j := 0) sel1 limit 16) t 7.4. Microsoft SQL Server (since 2005)
Another rather concise implementation of loops, this time with a recursive query.
with fibonacci(a, b) as ( select 1, 1 union all select b, a+b from fibonacci where b < 1000 ) SELECT cast(a as varchar)+', ' AS [text()] FROM fibonacci FOR XML PATH ('') 6. FP
FP is a prototype of all existing programming languages that use the programming-level programming paradigm (function-level, not to be confused with functional, that is, simply functional ). Invented in 1977, it is more a mathematical model than a real programming language: it did not even have an official standard (except for the only article in which it is described), not to mention the implementation! However, in our time there are interpreters of this language, usually written in the framework of student work. One of them is Furry Paws , and its cozy name does not at all correspond to the "comfort" of its use.
Programming at the function level involves building a program from elementary functions that can be combined using functionals (functional forms). So, ~ 1 is an elementary function that always returns the value 1; id is a function that returns the value passed to it, [] is a functional form that combines its arguments into a sequence, etc.
one = eq.[id, ~1]
dec = sub.[id, ~1]
seq = one -> [~1] ; cat.[seq.dec, [id]]
fibonacci = lt.[id, ~3] -> ~1 ; add.[fibonacci.sub.[id, ~1], fibonacci.sub.[id, ~2]]
main = show.(return @fibonacci.(seq.~16))5. J
Another language that uses “function-level programming” is a worthy successor to FP. Interestingly, almost any expression on it can be written in several ways, from almost traditional to completely unnatural (as required in this article). So, for example, calculating Fibonacci numbers using the Binet formula can be written quite civilized:
load 'printf'
g =: 0.5 * (1 + 5 ^ 0.5)
fib =: (0.2 ^ 0.5) * (g &^ - (1-g) &^)
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf fib 1+i.16And you can replace almost all mathematical operations with their equivalents specific to J:
load 'printf'
g =: -: >: %:5
fib =: (%:5) %~ g&^ - (1-g)&^
fstr =: '...' ,~ ,~^:4 '%d, '
fstr printf fib"0 >:i.16And it will hardly be obvious to anyone that%: - is the extraction of the square root,>: - increment, -: - division by two, and% ~ - division, and when writing, the dividend and divisor are swapped.
Calculation using recursion:
load 'printf'
fibr=: 1:`(-&2 + &fibr -&1) @.(2&<)"0
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf fibr 1+i.164. Hanoi Love
A little-known esoteric language, interesting for its minimalism and the use of a stack-based memory model. Unlike the following language, the main difficulty lies not in performing arithmetic operations, but in obtaining the contents of precisely those stack elements that are needed at each step. Printing, however, is also unpleasant, so only the first six numbers are calculated and displayed.
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;.'...;;;;;;;;;;;;.'...,..''''''..`.'.
..;.'.,.'...:...,.'..;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
"'.,.'...,"'.'...,"''.,...'.,..'..,...'...;.'.,.,!...,,,...;;"'"'"'Language descriptions and comments on the given code can be found on the Hanoi Love page.
3. Brainfuck
Classic esoteric programming genre - Brainfuck. A language in which even copying or addition is not an elementary operation, printing
a three-digit number is worthy of a separate ode, and using it to solve a specific task is a masochist’s dream: well ;-)
In the authoring interpreter (Muller's Brainfuck) the contents of memory cells are stored in variables of type byte, and the Fibonacci numbers from the 14th to the 16th would cause an overflow of memory. The implementation of long arithmetic on Brainfuck is no longer a symptom, but practically a diagnosis, therefore, when writing a solution, it was assumed that the memory cell can store numbers up to 1000 (in many implementations of the language, quite capacious data types are used for storage).
++++++++++++++++++++++++++++++++++++++++++++>++++++++++++++++++++++++
++++++++>++++++++++++++++>>+<<[>>>>++++++++++<<[->+>-[>+>>]>[+[-<+>]>
+>>]<<<<<<]>[<+>-]>[-]>>>++++++++++<[->-[>+>>]>[+[-<+>]>+>>]<<<<<]>[-
]>>[++++++++++++++++++++++++++++++++++++++++++++++++.[-]]<[++++++++++
++++++++++++++++++++++++++++++++++++++.[-]]<<<+++++++++++++++++++++++
+++++++++++++++++++++++++.[-]<<<<<<<.>.>>[>>+<<-]>[>+<<+>-]>[<+>-]<<<
-]<<++...Language descriptions and comments on the code can be found on the Brainfuck page.
2. Brainloller
The simplest of the graphic dialects of Brainfuck, invented by Lode Vandevenne.
Programs are read from PNG pictures, commands are written in pixels of different colors, and eight more commands are added to eight commands in Brainfuck - control of the pointer to the current pixel. To all the delights of Brainfuck, the complete unreadability of the “code” and the complete impossibility are added.
“Encode” without ancillary tools (for example, a converter of programs and pictures).
The author's interpreter of the language has sunk into oblivion, so for the generation of the “program” I had to write my own. The “program” is shown in a tenfold increase.
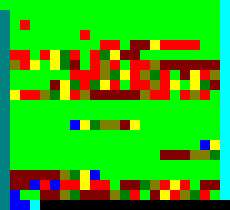
1. Unary
Where is worse? - the reader will think, flipping through the screen with a quivering hand Yes, it gets worse. In previous languages, the program could at least embrace the eye, and this is already a lot.
Meet the winner of the rating - Unary. The Brainfuck dialect, invented by the same Lode Vandevenne (oh, Monsieur knows a lot about perversions!), Assumes that Brainfuck commands are converted into binary codes and concatenated into one binary number, the unary record of which is a program on Unary. The program for generating Fibonacci numbers is a string of
167967665105731198557055496639385943332278803897935697536099438828197
665241403160165880863622431582784595268769268183940269756210147305655
704025762911607244068691728105306566342622386432823429136972542304655
647901781271798433263001837026612851345264031562174039657802748245705
398528237993320520942720239597540583536934220029626573406470088757427
393143000966310611249037587993216365993804186165097620168960460854977
571944373603975793034586829061577464233522714007498991416860375267535
193648636795096472789203729505034887001634966681420589637468649908257
407260923590831776308356684326657774592110098643361324426156431864437
942781495979555960608253552679248495326880775320385281559763269974848
026839024530519989287202261977272377723622502479809174132505837648641
033569945906182518892142219706483917757108086522763280388915772444727
238483811923456440363260610571471034139736312976255142288379411989404
9017738035 (that is, approximately 1.68 * 10 ^ 906) zeros.
I am sure that the languages listed here are far from the worst thing a programmer may encounter (in any case, not all of them :-)), but I'm not a magician, I'm just learning.
Source: https://habr.com/ru/post/94421/
All Articles