Eric Lippert - Generation of all arbitrary trees

Last time, we said that the number of binary trees with n vertices is C (n), where C (n) is the nth Catalan number. I became interested in something more: arbitrary trees from n vertices or binary trees from n vertices. The answer may surprise you, it does not lie on the surface.


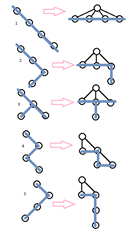
I will immediately receive the common answer to this question: “Of course, there are more arbitrary trees, because a binary tree is a special case of an arbitrary tree. ” Can you say why this is wrong? There are more binary trees than arbitrary trees! There are two binary trees of two vertices: one with the left descendant of the child of the root, and the other with the right descendant of the root. But there is only one arbitrary tree with two vertices, in it there is no difference between the “left” and the “right” descendant.

As it turned out, the answer to my question (except for degenerate cases of trees from zero vertices and one vertex) is that there are always more binary trees from n vertices than arbitrary trees from n vertices.

If you investigate this problem, you will notice an interesting fact: the number of arbitrary trees from n vertices is equal to (n-1). There are 14 binary trees from 4 peaks and 14 arbitrary trees from 5 peaks. There are 1,430 binary trees from 8 peaks and 1,430 arbitrary trees from 9 peaks. Wonderful!
')
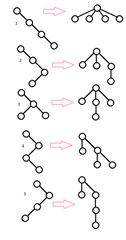
Obviously, this cannot be a coincidence. There should be a one-to-one correspondence between binary trees of size n and arbitrary trees of size n + 1. Indeed, it is easy to verify the existence of a correspondence if you look at the pictures. On the left is an image of the first 5 binary trees of size 4, and next is five corresponding arbitrary trees of size 5.

To make the match more understandable, look at the image on the right. To go from a binary tree to the corresponding arbitrary tree, you need to rotate the binary tree 45 degrees counterclockwise, add the root from above, and then fix all the horizontal lines so that they point to the parents.

Or, from the point of view of data structures, each vertex in an arbitrary tree can be represented as a link to the first child and a link to the next brother. It turned out exactly the binary tree, but instead of the inscriptions on the tops “first child” and “next brother” you need to write “left descendant” and “right descendant”. There is only one difference between a binary tree and an arbitrary tree in this system - the right descendant of the root is always empty, since root has no brothers. Now you lead that the difference between a binary tree and an arbitrary tree is in the field names in the data structure, which means we showed a one-to-one correspondence between them.

Thus, we received the solution of the second part of my problem. We have a mechanism that numbers all binary trees and a one-to-one correspondence between binary trees and arbitrary trees. All that remains to be done is to get the mechanism for turning a binary tree into the corresponding arbitrary tree. Let us leave this as an exercise, but for the sake of interest, we present here a mechanism that turns a binary tree into a string representation of the corresponding arbitrary tree, using the compact syntax for an arbitrary tree I spoke of last time.

public static string TreeString(Node node)
{
//
// .
var sb = new StringBuilder ();
Action<Node> f = null ;
f = n =>
{
sb.Append( "{" );
for (Node child = n.Left; child != null ; child = child.Right)
f(child);
sb.Append( "}" );
};
f( new Node(node, null ));
return sb.ToString();
}

* This source code was highlighted with Source Code Highlighter .

To obtain all trees of size 5, we will iterate over all binary trees of size 4 and derive the corresponding arbitrary trees of size 5.

foreach ( var n in AllBinaryTrees(4))
Console .WriteLine(TreeString(n));

* This source code was highlighted with Source Code Highlighter .

and we will get
{{} {} {} {}}
{{} {} {{}}}
{{} {{}} {}}
{{} {{} {}}}
{{} {{{}}}}
{{{}} {} {}}
{{{}} {{}}}
{{{} {}} {}}
{{{{}}} {}}
{{{} {} {}}}
{{{} {{}}}}
{{{{}} {}}}
{{{{} {}}}}
{{{{{}}}}}


Please note that if you remove the extreme brackets, we will get a solution to the problem “print all the right combinations of four pairs of brackets”! If you enumerate all binary trees, then you enumerate all the solutions of many different equivalent problems.

Next time: what can we generate more?