Circuitry. Minimization of logic functions
The minimization of logical functions is one of the typical tasks in the process of learning circuitry. Therefore, I believe that such an article takes place, I hope you will like it.

The complexity of the logical function, and hence the complexity and cost of the scheme (chain) that implements it, is proportional to the number of logical operations and the number of occurrences of variables or their negations. In principle, any logical function can be simplified directly with the help of the axioms and theorems of logic, but, as a rule, such transformations require cumbersome calculations.
In addition, the process of simplifying Boolean expressions is not algorithmic. Therefore, it is more expedient to use special algorithmic minimization methods that allow simplifying the function more simply, quickly and accurately. Such methods include, for example, the Quine method, the Carnot map method, the implicant test method, the implicative matrix method, the Quine-McClasky method, etc. These methods are most suitable for common practice, especially minimizing a logical function using Carnot maps. The Carnot map method maintains visibility when the number of variables is no more than six. In cases where the number of arguments is more than six, the Quine-MacClasky method is usually used.
In the process of minimization of a logical function, it is usually taken into account in which basis it will be more efficient to implement its minimum form using electronic circuits.
')
The Karno map is a graphical way to minimize switching (boolean) functions, ensuring the relative ease of working with large expressions and eliminating potential races. It is a pairwise incomplete bonding and elemental absorption. Carnot maps are treated as a function table restructured accordingly. Carnot maps can be considered as a certain flat sweep of an n-dimensional Boolean cube.
Carnot maps were invented in 1952 by Edward V. Weich and improved in 1953 by Maurice Carnot, a physicist at Bell Labs, and were designed to help simplify digital electronic circuits.
In the Karno map, Boolean variables are transferred from the truth table and are ordered using the Gray code, in which each successive number differs from the previous one only in one digit.
The main method of minimizing logical functions represented as SDNF or SKNF is the operation of pairwise incomplete gluing and elemental absorption. The pair-gluing operation is carried out between two terms (members) containing the same variables, the occurrences of which (direct and inverse) coincide for all variables, except one. In this case, all variables, except one, can be put out of the brackets, and the remaining in brackets the direct and inverse occurrences of one variable can be glued together. For example:

The possibility of absorption follows from the obvious equalities.

Thus, the main task in minimizing SDNF and SKNF is the search for terms suitable for gluing and subsequent absorption, which for large forms can be quite a challenge. Carnot maps provide a visual way to find such terms.
As is known, the Boolean functions of N variables, represented as SDNF or SKNF, can have 2N different terms. All these terms constitute a structure topologically equivalent to an N-dimensional cube, and any two terms connected by an edge are suitable for gluing and absorption.
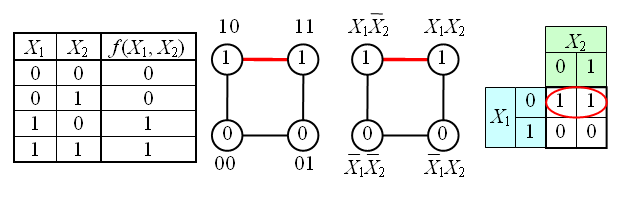
The figure shows a simple truth table for a function of two variables, a 2-dimensional cube (square) corresponding to this table, as well as a 2-dimensional cube with the designation of the members of the PDNF and an equivalent table for grouping terms:
In the case of a function of three variables, one has to deal with a three-dimensional cube. It is more complicated and less obvious, but technically possible. The figure shows, as an example, the truth table for a Boolean function of three variables and the corresponding cube.
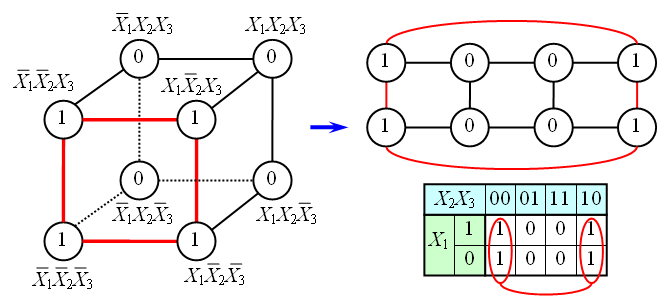
As can be seen from the figure, more complex configurations of terms are possible for the three-dimensional case. For example, four terms belonging to one face of a cube are combined into one term with the absorption of two variables:

In the general case, we can say that 2K terms belonging to one K-dimensional face of a hypercube are glued together into one term, while K variables are absorbed.
To simplify the work with Boolean functions of a large number of variables, the following convenient technique was proposed. The cube, which is a structure of terms, turns on a plane as shown in the figure. Thus, it is possible to represent Boolean functions with more than two variables in a flat table. It should be remembered that the order of the codes of the terms in the table (00 01 11 10) does not correspond to the order of the binary numbers, and the cells in the extreme columns of the table are adjacent to each other.

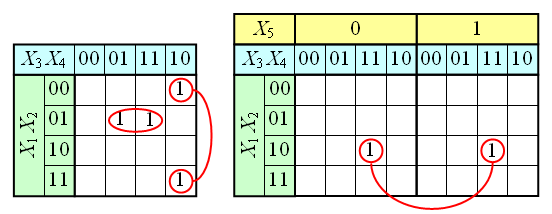
Similarly, you can work with the functions of four, five or more variables. Examples of tables for N = 4 and N = 5 are shown in the figure. For these tables, it should be remembered that the adjacent cells are in the corresponding cells of the outermost columns and the corresponding cells of the upper and lower rows. For tables 5 and more variables, it is also necessary to take into account that the 4x4 squares are virtually on top of each other in the third dimension, therefore the respective cells of two adjacent 4x4 squares are adjacent, and the terms corresponding to them can be glued together.
A Carnot map can be compiled for any number of variables, but it is convenient to work with a number of variables of no more than five. In essence, the Carnot Map is a truth table compiled in a 2-dimensional view. Thanks to the use of the Gray code, the top line is adjacent to the bottom, and the right column is adjacent to the left, so the entire Karno Map is collapsed into a torus (donut) shape. At the intersection of the row and the column is put down the corresponding value from the truth table. After the map is full, you can proceed to minimize.
If it is necessary to obtain the minimum DNF, then in the Map we consider only those cells that contain units, if we need CNF, then we consider those cells that contain zeros. The minimization itself is performed according to the following rules (for example, DNF):
Next, we take the first region and see which variables do not change within this region, write out the conjunction of these variables, if the unchanging variable is zero, we place an inversion above it. We take the next area, perform the same as for the first, and so on for all areas. The conjunction of areas is combined by disjunction.
For example (for Maps on 2 variables):
For KNF, everything is the same, only we consider cells with zeros, unchanging variables within one region are combined into disjunctions (inversions are put over unit variables), and disjunctions of areas are combined into a conjunction. At this minimization is considered complete. So for the Carnot Map in Figure 1, the expression in the DNF format will look like:
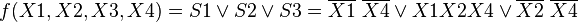
In CNF format:


Why do you need it?
The complexity of the logical function, and hence the complexity and cost of the scheme (chain) that implements it, is proportional to the number of logical operations and the number of occurrences of variables or their negations. In principle, any logical function can be simplified directly with the help of the axioms and theorems of logic, but, as a rule, such transformations require cumbersome calculations.
In addition, the process of simplifying Boolean expressions is not algorithmic. Therefore, it is more expedient to use special algorithmic minimization methods that allow simplifying the function more simply, quickly and accurately. Such methods include, for example, the Quine method, the Carnot map method, the implicant test method, the implicative matrix method, the Quine-McClasky method, etc. These methods are most suitable for common practice, especially minimizing a logical function using Carnot maps. The Carnot map method maintains visibility when the number of variables is no more than six. In cases where the number of arguments is more than six, the Quine-MacClasky method is usually used.
In the process of minimization of a logical function, it is usually taken into account in which basis it will be more efficient to implement its minimum form using electronic circuits.
')
Minimizing Logic Functions with Carnot Maps
The Karno map is a graphical way to minimize switching (boolean) functions, ensuring the relative ease of working with large expressions and eliminating potential races. It is a pairwise incomplete bonding and elemental absorption. Carnot maps are treated as a function table restructured accordingly. Carnot maps can be considered as a certain flat sweep of an n-dimensional Boolean cube.
Carnot maps were invented in 1952 by Edward V. Weich and improved in 1953 by Maurice Carnot, a physicist at Bell Labs, and were designed to help simplify digital electronic circuits.
In the Karno map, Boolean variables are transferred from the truth table and are ordered using the Gray code, in which each successive number differs from the previous one only in one digit.
The main method of minimizing logical functions represented as SDNF or SKNF is the operation of pairwise incomplete gluing and elemental absorption. The pair-gluing operation is carried out between two terms (members) containing the same variables, the occurrences of which (direct and inverse) coincide for all variables, except one. In this case, all variables, except one, can be put out of the brackets, and the remaining in brackets the direct and inverse occurrences of one variable can be glued together. For example:

The possibility of absorption follows from the obvious equalities.

Thus, the main task in minimizing SDNF and SKNF is the search for terms suitable for gluing and subsequent absorption, which for large forms can be quite a challenge. Carnot maps provide a visual way to find such terms.
As is known, the Boolean functions of N variables, represented as SDNF or SKNF, can have 2N different terms. All these terms constitute a structure topologically equivalent to an N-dimensional cube, and any two terms connected by an edge are suitable for gluing and absorption.
The figure shows a simple truth table for a function of two variables, a 2-dimensional cube (square) corresponding to this table, as well as a 2-dimensional cube with the designation of the members of the PDNF and an equivalent table for grouping terms:

In the case of a function of three variables, one has to deal with a three-dimensional cube. It is more complicated and less obvious, but technically possible. The figure shows, as an example, the truth table for a Boolean function of three variables and the corresponding cube.

As can be seen from the figure, more complex configurations of terms are possible for the three-dimensional case. For example, four terms belonging to one face of a cube are combined into one term with the absorption of two variables:

In the general case, we can say that 2K terms belonging to one K-dimensional face of a hypercube are glued together into one term, while K variables are absorbed.
To simplify the work with Boolean functions of a large number of variables, the following convenient technique was proposed. The cube, which is a structure of terms, turns on a plane as shown in the figure. Thus, it is possible to represent Boolean functions with more than two variables in a flat table. It should be remembered that the order of the codes of the terms in the table (00 01 11 10) does not correspond to the order of the binary numbers, and the cells in the extreme columns of the table are adjacent to each other.

Similarly, you can work with the functions of four, five or more variables. Examples of tables for N = 4 and N = 5 are shown in the figure. For these tables, it should be remembered that the adjacent cells are in the corresponding cells of the outermost columns and the corresponding cells of the upper and lower rows. For tables 5 and more variables, it is also necessary to take into account that the 4x4 squares are virtually on top of each other in the third dimension, therefore the respective cells of two adjacent 4x4 squares are adjacent, and the terms corresponding to them can be glued together.

A Carnot map can be compiled for any number of variables, but it is convenient to work with a number of variables of no more than five. In essence, the Carnot Map is a truth table compiled in a 2-dimensional view. Thanks to the use of the Gray code, the top line is adjacent to the bottom, and the right column is adjacent to the left, so the entire Karno Map is collapsed into a torus (donut) shape. At the intersection of the row and the column is put down the corresponding value from the truth table. After the map is full, you can proceed to minimize.
If it is necessary to obtain the minimum DNF, then in the Map we consider only those cells that contain units, if we need CNF, then we consider those cells that contain zeros. The minimization itself is performed according to the following rules (for example, DNF):
- We combine adjacent cells containing units into a region, so that one region contains 2 n ( n is an integer = 0 ...
 ) cells (remember that the extreme rows and columns are adjacent to each other), in the area should not be cells containing zeros;
) cells (remember that the extreme rows and columns are adjacent to each other), in the area should not be cells containing zeros; - The area should be located symmetrically to the axis (s) (the axes are located every four cells);
- Not adjacent areas symmetrically located axis (s) can be combined into one;
- The area should be as large as possible, and the number of areas as small as possible;
- Areas may intersect;
- There are several possible cover options.
Next, we take the first region and see which variables do not change within this region, write out the conjunction of these variables, if the unchanging variable is zero, we place an inversion above it. We take the next area, perform the same as for the first, and so on for all areas. The conjunction of areas is combined by disjunction.
For example (for Maps on 2 variables):
 |  |  |  |  |  |  |  | |||||||
 |  |  |  |  |  |  |  | |||||||
 |  |  |  |  |  | |||||||||
 |  |  |  |  |  | |||||||||
 |  |  |  |  |  | |||||||||
 |  |
For KNF, everything is the same, only we consider cells with zeros, unchanging variables within one region are combined into disjunctions (inversions are put over unit variables), and disjunctions of areas are combined into a conjunction. At this minimization is considered complete. So for the Carnot Map in Figure 1, the expression in the DNF format will look like:
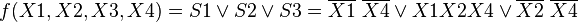
In CNF format:

Source: https://habr.com/ru/post/93296/
All Articles