Processor Cache Effects Gallery

Almost all developers know that the processor's cache is such a small, but fast memory, which stores data from recently visited areas of memory - the definition is short and fairly accurate. However, knowledge of the “boring” details about the mechanisms of the cache is necessary to understand the factors affecting the performance of the code.

In this article, we will look at a number of examples illustrating various features of the operation of caches and their impact on performance. Examples will be in C #, the choice of language and platform does not so much affect the performance assessment and the final conclusions. Naturally, within reasonable limits, if you select a language in which reading a value from an array is equivalent to referring to a hash table, you will not get any interpretable results. Italics are translator's notes.

  - - - habracut - - - 

Example 1: memory access and performance

How much do you think the second cycle is faster than the first?
')

int [] arr = new int [64 * 1024 * 1024];

//
for ( int i = 0; i < arr.Length; i++) arr[i] *= 3;

//
for ( int i = 0; i < arr.Length; i += 16) arr[i] *= 3;

The first loop multiplies all array values ​​by 3, the second loop only every sixteenth value. The second cycle performs only 6% of the first cycle, but on modern machines both cycles are performed in approximately equal time: 80 ms and 78 ms, respectively (on my machine).

The answer is simple - access to memory. The speed of these cycles in the first place is determined by the speed of the memory subsystem, and not the speed of the integer multiplication. As we will see in the following example, the number of memory accesses is the same in both the first and second cases.

Example 2: Cache String Effects

Let's dig deeper - let's try other step values, not just 1 and 16:

for ( int i = 0; i < arr.Length; i += K /* */ ) arr[i] *= 3;

Here is the run time of this cycle for different values ​​of step K:



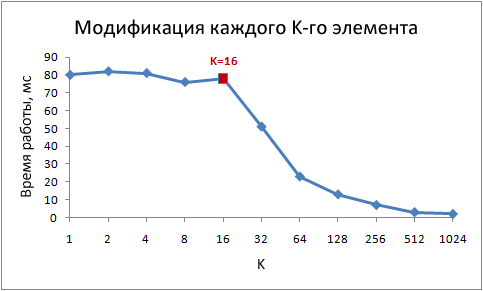
Note that with step values ​​from 1 to 16, the running time remains almost unchanged. But with values ​​greater than 16, the running time is approximately halved each time we double the step. This does not mean that the cycle somehow starts to work faster, just the number of iterations also decreases. The key point is the same running time with step values ​​from 1 to 16.

The reason for this is that modern processors access memory not byte-by-bye, but in small blocks called cache lines. Typically, the string size is 64 bytes. When you read a value from memory, at least one cache line is cached. Subsequent access to any value from this string happens very quickly.

Due to the fact that 16 values ​​of type int occupy 64 bytes, cycles with steps from 1 to 16 refer to the same number of cache lines, more precisely, to all the lines of the array cache. At step 32, every second line is addressed, at step 64, every fourth line.

Understanding this is very important for some optimization methods. From the location of the data in memory depends on the number of calls to it. For example, due to unaligned data, it may take two memory accesses, instead of one. As we found out above, the speed of work will be two times lower.

Example 3: Cache sizes of the first and second level (L1 and L2)

Modern processors, as a rule, have two or three levels of caches, usually they are called L1, L2 and L3. In order to find out the sizes of caches at various levels, you can use the CoreInfo utility or the Windows API API function GetLogicalProcessorInfo . Both methods also provide information about the size of the cache line for each level.

On my machine, CoreInfo reports L1 data caches with a size of 32 KB, L1 instruction caches with a capacity of 32 KB each, and L2 data caches with a capacity of 4 MB. Each core has its own personal L1 caches, L2 caches are common for each pair of cores:

  Logical Processor to Cache Map:
 * --- Data Cache 0, Level 1, 32 KB, Assoc 8, LineSize 64
 * --- Instruction Cache 0, Level 1, 32 KB, Assoc 8, LineSize 64
 - * - Data Cache 1, Level 1, 32 KB, Assoc 8, LineSize 64
 - * - Instruction Cache 1, Level 1, 32 KB, Assoc 8, LineSize 64
 ** - Unified Cache 0, Level 2, 4 MB, Assoc 16, LineSize 64
 - * - Data Cache 2, Level 1, 32 KB, Assoc 8, LineSize 64
 - * - Instruction Cache 2, Level 1, 32 KB, Assoc 8, LineSize 64
 --- * Data Cache 3, Level 1, 32 KB, Assoc 8, LineSize 64
 --- * Instruction Cache 3, Level 1, 32 KB, Assoc 8, LineSize 64
 - ** Unified Cache 1, Level 2, 4 MB, Assoc 16, LineSize 64 

Let's verify this information experimentally. To do this, go through our array, incrementing every 16th value — an easy way to change the data in each cache line. Upon reaching the end, we return to the beginning. Check the different sizes of the array, we should see a drop in performance when the array ceases to fit into caches of different levels.

The code is:

int steps = 64 * 1024 * 1024; //
int lengthMod = arr.Length - 1; // --

for ( int i = 0; i < steps; i++)
{
// x & lengthMod = x % arr.Length,
arr[(i * 16) & lengthMod]++;
}


Test results:



On my machine, performance drops after 32 KB and 4 MB, which are the sizes of L1 and L2 caches.

Example 4: instruction concurrency

Now let's take a look at something else. In your opinion, which of these two cycles will execute faster?

int steps = 256 * 1024 * 1024;
int [] a = new int [2];

//
for ( int i = 0; i < steps; i++) { a[0]++; a[0]++; }

//
for ( int i = 0; i < steps; i++) { a[0]++; a[1]++; }

It turns out that the second cycle runs almost twice as fast, at least on all the machines I tested. Why? Because the commands inside the cycles have different data dependencies. The commands of the first have the following dependency chain:



In the second cycle, the dependencies are as follows:



The functional parts of modern processors are capable of performing a certain number of some operations at the same time, as a rule, not a very large number. For example, parallel access to data from the L1 cache is possible at two addresses, it is also possible to simultaneously execute two simple arithmetic commands. In the first cycle, the processor cannot use these features, but it can in the second.

Example 5: Cache Associativity

One of the key questions that needs to be answered when designing a cache is whether data from a specific area of ​​memory can be stored in any cache cells or only in some of them. Three possible solutions:

1. The direct mapping cache , the data of each cache line in RAM is stored in only one predefined cache cell. The simplest way to calculate a mapping is index_strings_in_memory% number_caches_caches. Two lines mapped to the same cell cannot be located in the cache at the same time.
   
   
2. N-input partially associative cache , each row can be stored in N different cache cells. For example, in a 16-entry cache, a string can be stored in one of the 16 cells that make up a group. Usually, rows with equal low bits of indices divide one group.
   
   
3. Fully associative cache , any string can be stored in any cache cell. The solution is equivalent to a hash table in its behavior.

Forward mapping caches are prone to conflicts, for example, when two lines compete for one cell, alternately pushing each other out of the cache, the efficiency is very low. On the other hand, fully associative caches, although they lack this drawback, are very complex and expensive to implement. Partially associative caches are a typical trade-off between implementation complexity and efficiency.

For example, on my machine, the 4MB L2 cache is a 16-way partially associative cache. All RAM is divided into sets of rows by the lower bits of their indices; rows from each set compete for one group of 16 L2 cache cells.

Since the L2 cache has 65,536 cells (4 * 2 20/64) and each group consists of 16 cells, we have a total of 4,096 groups. Thus, the lower 12 bits of the row index determine to which group this row belongs (2 ¹² = 4,096). As a result, lines with multiples of 262,144 (4,096 * 64) share the same group of 16 cells and compete for a place in it.

To make associative effects manifest themselves, we need to constantly access a large number of lines from one group, for example, using the following code:

public static long UpdateEveryKthByte( byte [] arr, int K)
{
const int rep = 1024 * 1024; //

Stopwatch sw = Stopwatch.StartNew();

int p = 0;
for ( int i = 0; i < rep; i++)
{
arr[p]++;

p += K; if (p >= arr.Length) p = 0;
}

sw.Stop();
return sw.ElapsedMilliseconds;
}


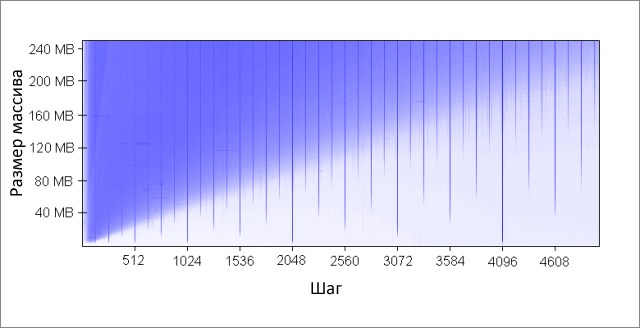
The method increments each Kth array element. Upon reaching the end, we start again. After a fairly large number of iterations (2 ²⁰ ), we stop. I made runs for various array sizes and step values ​​K. Results (blue is a long time, white is a small one):



The blue areas correspond to those cases where, with constant data changes, the cache is not able to hold all the required data at the same time . A bright blue color indicates an operating time of about 80 ms, almost white - 10 ms.

Understand the blue areas:

1. Why do vertical lines appear? Vertical lines correspond to the step values ​​at which too many lines (more than 16) from one group are accessed. For these values, the 16-input cache of my machine cannot hold all the necessary data.
   
   Some of the bad step values ​​are powers of two: 256 and 512. For example, consider step 512 and an 8 MB array. At this step, in the array there are 32 sections (8 * 2 20/262 144), which fight with each other for cells in 512 cache groups (262 144/512). Section 32, and the cells in the cache for each group is only 16, so there is not enough space for everyone.
   
   Other step values, which are not powers of two, are simply unlucky, which causes a large number of calls to the same cache groups, as well as vertical blue lines in the figure. At this point, number theory lovers are invited to ponder.
   
   
2. Why do vertical lines break at the 4 MB border? With an array size of 4 MB or less, the 16-input cache behaves in the same way as a fully associative cache, that is, it can hold all the data in the array without conflicts. There are no more than 16 areas leading for one cache group (262,144 * 16 = 4 * 2 ²⁰ = 4 MB).
   
   
3. Why is there a big blue triangle in the upper left? Because with a small step and a large array of cache is not able to fit all the necessary data. The degree of cache associativity plays a minor role here, the limitation is related to the size of the L2 cache.
   
   For example, with an array size of 16 MB and step 128, we access every 128th byte, thus modifying every other line in the array cache. To save every second line in the cache, its size is 8 MB, but on my machine there is only 4 MB.
   
   Even if the cache were fully associative, it would not allow 8 MB of data to be stored in it. Note that in the example already considered in 512 steps and an 8 MB array size, we only need 1 MB of cache to save all the necessary data, but this cannot be done due to insufficient cache associativity.
   
   
4. Why is the left side of the triangle gradually gaining its intensity? The maximum intensity falls on a step value of 64 bytes, which is equal to the size of the cache line. As we saw in the first and second examples, sequential access to the same line is practically worthless. For example, at a step of 16 bytes, we have four memory accesses for the price of one.
   
   Since the number of iterations is equal in our test for any step value, the cheaper step as a result gives less work time.
   

The detected effects are also saved for large values ​​of the parameters:



Cache associativity is an interesting thing that can manifest itself under certain conditions. Unlike the other problems discussed in this article, it is not so serious. Definitely, this is not something that requires constant attention when writing programs.

Example 6: False Cache Sharing

On multi-core machines, you may encounter another problem - matching caches. The processor cores have partially or completely separate caches. On my machine, L1 caches are separate (as usual), there are also two L2 caches that are common to each pair of cores. Details may vary, but in general modern multi-core processors have multi-level hierarchical caches. And the fastest, but also the smallest caches, belong to the individual cores.

When one of the kernels modifies a value in its cache, the other kernels can no longer use the old value. The value in the caches of other cores should be updated. Moreover, the entire cache line must be updated completely , since the caches operate on data at the row level.

We demonstrate this problem in the following code:

private static int [] s_counter = new int [1024];

private void UpdateCounter( int position)
{
for ( int j = 0; j < 100000000; j++)
{
s_counter[position] = s_counter[position] + 3;
}
}

If on my four core machine I call this method with parameters 0, 1, 2, 3 out of four threads simultaneously, then the runtime will be 4.3 seconds . But if I call the method with parameters 16, 32, 48, 64, then the running time will be only 0.28 seconds .

Why? In the first case, all four values ​​processed by the threads at each time point are likely to fall into one cache line. Each time one core increases the next value, it marks cache cells that contain this value in other cores as invalid. After this operation, all other kernels will have to re-cache the string. This makes the caching mechanism unworkable, killing performance.

Example 7: Iron Complexity

Even now, when the principles of the cache is not a secret for you, iron will still present you surprises. Processors differ from each other by optimization methods, heuristics, and other subtleties of implementation.

The L1 cache of some processors can provide parallel access to two cells, if they belong to different groups, but if they belong to one, only sequentially. As far as I know, some may even have parallel access to different quarters of the same cell.

Processors may surprise you with cunning optimizations. For example, the code from the previous example about false cache sharing does not work on my home computer as it was intended - in the simplest cases, the processor can optimize performance and reduce negative effects. If the code is slightly modified, everything falls into place.

Here is another example of strange iron fads:

private static int A, B, C, D, E, F, G;

private static void Weirdness()
{
for ( int i = 0; i < 200000000; i++)
{
<- >
}
}


If instead of <some code> substitute three different options, you can get the following results:



Incrementing A, B, C, D fields takes more time than incrementing A, C, E, G fields. What's even weirder, incrementing A and C fields takes longer than A, C and E fields, G. I don’t know for sure what are the reasons for this, but perhaps they are connected with memory banks ( yes, with the usual three-liter savings banks of memory, and not what you thought ). Having thoughts on this, please comment in the comments.

I have not observed the above described on the machine, however, sometimes there are abnormally bad results - most likely, the task scheduler makes its own “corrections”.

From this example, the following lesson can be learned: it is very difficult to completely predict the behavior of iron. Yes, you can predict a lot, but you need to constantly confirm your predictions with the help of measurements and testing.

Conclusion

I hope that all of the above helped you understand the device caches of processors. Now you can use this knowledge in practice to optimize your code.

* Source code was highlighted with Source Code Highlighter .