"Difficult password" does not need decryption

I skipped over here a topic about "complex" passwords . Unfortunately, I see, many have taken this “method” seriously ...

Using encryption cards is not a reliable method! As it was correctly noted in the comments there - “our grandfathers used it in the war” ... But they used more advanced methods.

The method cited in that article can NOT be used in any way (!) , The passwords for this method are completely decrypted , you just give them to attackers on a silver platter! And now I will prove it ...
')

Complexity and parameters

In total, 36 tables can exist using this method, which is as complex as a password of one letter or number. The differences of the tables in only one parameter : the shift to the left by [0-35] is the number of columns equal to the interval “a-z0-9”.

You can check: table one is z = (i+j -1 ) % 36 , the second is z=(i+j +9 ) % 36 , where i and j take the values: “a” = 0, “b” = 1, "c" = 2, ... Check for any other values ​​- the difference is only in one constant, even though the second table in the row starts with "s" (which in general, since mathematics did not make sense) .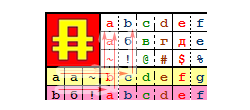

  first:
 a + b + -1 = a (0 + 1 + -1 = 0)
 a + c + -1 = b (0 + 2 + -1 = 1)
 b + a + -1 = a (1 + 0 + -1 = 0)

 second:

  a + j + 9 = s (0 + 9 + 9 = 18)
 a + k + 9 = t (0 + 10 + 9 = 19)
 b + i + 9 = s (1 + 8 + 9 = 18)

  0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
  abcdefghijklmnopqr

 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
  stuvwxyz 0 1 2 3 4 5 6 7 8 9 

Therefore, knowing the encrypted password and the name of the resource - we have only 36 of the original passwords .

The final example of the original text (about him and below):



By the way, the minus is immediately visible - it is difficult for people to use tablets, mistakes are inevitable. This is a password encrypted by the author of that article. There is an error in it - “aa” in the second position - this is “9” on the first plate , and not “b”.

We decrypt (correctly) the encrypted password ...
Here are some of the 36 passwords (corresponding to 36 different table offsets and names - “habrahabr”):
+5 j4mmqil7j
+4 k5nnrjm8k
+3 l6ooskn9l
+2 m7pptloam
+1 n8qqumpbn
+0 o9rrvnqco
-1 passwordp
-2 qbttxpseq
-3 rcuuyqtfr
-4 sdvvzrugs
-5 teww0svht
-1 - this is the desired constant offset table.

Yes, this is a real “decryption”, yes, the program was written ... at the end of the “p” because the repeat of the password begins.

Note that we need only one letter from the password and the same one - from the site name to get one variable (offset).

Small letters in the "encrypted" password will pass what letters will be vowels in the name of the site (reducing cryptographic strength).

So from the above, if we do not know the name of the site, but we know where there is a vowel (and it will be where there are small letters in the encrypted password) , then we have (one letter) = 36 (plates) * 6 (vowels = a, e, i, o, u, y) - 216 passwords ( without knowing the name of the site! ). Quite a bit, but in reality, see below (" In reality ") - most likely there will be only one.

Large letters do not change anything at all, except that they should be done back in small ones ( they do not add complexity ).

Dobivka somewhat complicates the task, but not in the example . Since the name of the resource is longer than the password, it turns out to decipher the short password (knowing the encrypted password and the name of the resource), which will go further along the cycle - we will easily recover and the dobivka (we will know the top line and the bottom line - we will restore the middle line ... here, except for a pair of "characters" in the positions 4,8,16 (bars, dogs), about her - below).

In the worst (but not real) case, an attacker will have to go through 36 passwords to another site without haste to enter.

In reality : Of the 36 passwords, surely only one will look like the word (!) That you memorized, so in reality even brute force is not required. So the password will be known for sure .

Substitution with symbols

Retreat about the "characters." The author proposed to replace the letters of the received password in the positions 4,8,16 - with characters on the plate.

Punctuation marks would add complexity if it were not for another method vulnerability - the cyclical nature of the repetition of a password. The author has shifted the punctuation marks relative to the Latin. Well, this is a plus, yes, this is another difficulty parameter, but given that we know for sure that 4.8 and 16 characters are changing, then we can (by the length of the site name “habrahabr”) decipher the word “pas * wor * p "In the first tablet (that under" * "we do not know yet).

Now the trick is that the (4 + 8) = 12 position is the same letter as on “4” (the password goes around - these are both letters of “s” in the word “pas s (4) wordpas s ( 12) word "), but punctuation was not used at the 12th place!

Consequently, we can decipher the 12th letter and immediately recognize the 4th letter.

Knowing 4 encrypted letter and its corresponding punctuation - we linearly received a punctuation offset. From this offset, we immediately recognize the 8th letter and, as a bonus, the 16th (which is the same). FAIL!

True, if the author encrypted the 12th letter, and the password would be 7-digit - we would still decipher it (the repetition of the letter would be at 4 + 7 = 13th place).

If there is a “dobivka” - it will spoil the picture, but not much, again - most of the dobivka will be deciphered (we will already know the upper line completely or almost completely and the lower one - the average will be restored from it, except maybe (!) 1 -2 letters closed with punctuation, but there is already a search to save - even * 36 options - a bit (and this is rarely the case that the punctuation successfully closes the letters that they cannot be restored from a repeated password).

The option is even worse

Knowing the encrypted passwords on two sites (+ the names of these two sites) - we will completely restore the original password and the tablet too.

Roughly speaking as a system of equations

x + Y1 + t = Z1,
x + Y2 + t = Z2,

where x = initial password
Y1, Y2 = name of resources (known)
t is the offset of the table
Z1, Z2 = encrypted password (known).

Two equations, two unknowns - the system is linear and has one solution for x and t.

In fact, one letter from both passwords and the same letter of the site names is enough. (Only one unknown value is the shift of the table to the left)

Here you don’t even have to go through - the password will be known for sure .

Conclusion

The encryption algorithm given in the original article is analogous to an alphanumeric password of 1 (one!) Character (log ₃₆ 36 = 1).

If encrypted passwords from two sites are known, then this is not encryption at all.

Is it possible to complicate

Even if you strengthen the algorithm by using Russian letters and symbols (which move independently), even if you add a table shift not only horizontally but also vertically, and even reflections horizontally and vertically, you will receive: 36 * 36 * 36 * 36 * 36 * 2 * 2 = 240 million tables ... It looks scary?

In fact, this is similar to a simple alphanumeric password of about 5 letters . That can hardly be considered "reliable" or "complex" (27 bits of encryption).

Strong encryption is 128 bits, which is approximately 14000000000000000000000000000 times should have more options than the “complicated” 240 million ( exactly ?) This is equivalent to a 25-letter alphanumeric password. (log ₃₆ ( ^2,128 ) = 24.75)

The only way this can really be “strengthened” is if:

1) First, the plate will be “reversed” (now it’s necessary to go vertically, and then go along this line with your finger, but you need to make an “encrypted” symbol at the intersection of the vertical and horizontal stripes) - this will reduce the repeatability and predictability, which is now maximum
2) Rows and columns need to be stretched so that there is no correspondence between the Latin and Russian symbols, everything is separated from each other - this will also reduce the repeatability and predictability,
3) The plate will contain only absolutely random numbers, digits and symbols in the body - and I mean absolutely random in each cell - no shifts in rows,
4) No repetition (password, site name),
5) No “positional” replacements.

However, even this tablet will not withstand a serious attack with long-term use (like all "tablets"). Once again: the use of encryption cards is not a reliable encryption method!

md5 ('site + key')

Many have advised this method. It is not bad, but it can be improved.

In fact, with sufficient power and memory for RainbowTables there is a chance that there will be a key. (ma-aaaaaaaa alenky, but there are - only 103 billion passwords per second can go through one computer - so, for example, “password” + “habr” can be decrypted in 10 days and home computer)

It is better to do rounds of encryption, to put it simply - take site + key and encrypt it 6000 times right here md5 (md5 (md5 (... so 6000 times ...... md5 ('site + key') ....). This will not stop the attacker, but will seriously slow down, so that the attack becomes impractical.Read (in English) what KeePass writes about the rounds - it will explain very much why I say that.

  # Pseudocode:
 k = key + site
 for 0..6000 {
    k = md5 (k)
 }
 print k 

And this is deciphering 150 years, against 10 days for the usual md5 (site + key). But even once - this is a pretty good method.

Completion

So even very impressive looking algorithms turn out to be quite unstable.

Be careful, inventing and implementing encryption algorithms is one of the few areas in which you can only trust people who specialize in encryption (for years) and only algorithms that have been tested and approved by other experts in the industry.

And the best way to store passwords is, nevertheless, a password manager, such as KeePass and the like.


Yoi Haji
view from Habra