Independent study of circuit design. Abstract machine. Part 2
The article is written, compiled and compiled by Brotherofken . Thank him so much.
In the previous article I tried to set out all the basic definitions and principles in order to make this article as clear as possible. Everything did not fit, so I strongly advise you to read these files:
Basis , Basis2 , Minimization . Later in this article I left a few explanatory notes in italics.
In this article I will try to explain in accessible language what an abstract automaton is, how to present it. Since automata theory is full of mathematics and complex, I will try to write in human language so that an unprepared reader can understand what is being said.

Electronic digital circuits can be formally divided into 2 classes:
In other words, the first class is logical devices that process the input signal. The second elements have memory and react to the signal depending on the data entered into them.
')
The machine will have to implement some functions that are set by the developer. It can be a simple adder, it can implement a processor micro-command, select words from the main memory, or parse an expression.
In general, without going into details, the abstract automaton can be represented as follows:
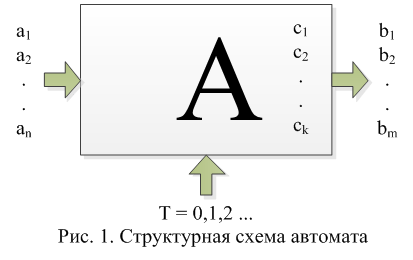
Or, if we move from an illustration to a mathematical description:
A = <A, B, C, δ, λ>
Legend:
δ and λ are not shown in the diagram for visual simplification.
Such an automaton functions discretely in time, that is, the values of the inputs, outputs, and the internal state of the automaton change at discrete points in time.
So, we have described in general terms what the Abstract Automaton is. An example of such an automaton may be a trigger, a computer register or an adder.
There are 2 types of machines:
As can be seen, the state of the automaton c (t) at the current time is a function of its state at the previous time and the input signal .
Automata differ by the type of exit function. In the Miles machine, the output signal is determined by the input signal a (t) and the state of the machine at the previous time instant c (t-1). The output of Moore’s automaton is determined by the pair of the input signal a (t) and the current state c (t).
It can also be noted that from one type you can go to the second and vice versa, and during the transition from the Mile to the Moore, the number of internal states of the automaton will remain the same, and during the reverse transition the number of internal states may increase. We will not dwell on this in detail, considering that we have synthesized (drew a graph) an automaton of the type that is needed.
So, on this with materiel over. Let's try to describe automata.
Those. an automatic machine of the type Miles produces an output signal when it changes its input, depending on its previous state. In this case, the duration of the output signal does not depend on the duration of the input signal, but only on its presence. In Moore type automata, the output signal depends on the state of the automaton at the current time, i. the machine will generate a certain output signal until it changes its state.
As we found out in the first part, an automaton is a set of input and output alphabets, a set of internal states and functions defining transitions and exits. However, usually the functions δ and λ are not specified, and the behavior of the automaton has to be described differently.
There are two main ways to set the machine:
An automaton graph is a directed connected graph whose vertices symbolize the internal states of the automaton, and arcs represent transitions from one state to another.
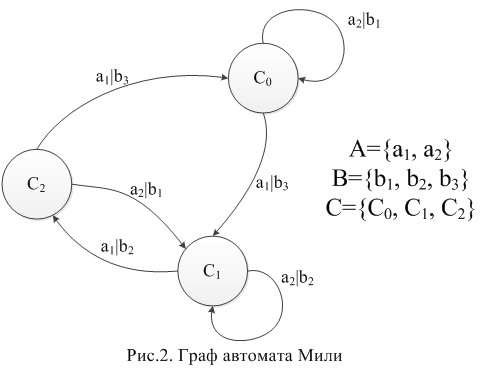
For the Miles graph on arcs, similar and output letters are indicated. The output letters are written over the arcs, symbolizing that the output state depends on the state of the machine at the previous time.

For the graph of Moore’s automaton, only input letters are written on arcs, while the output is indicated near the vertices.
Important point: If from each vertex there are as many arcs as there are input letters, then the automaton is called complete . In other words, if there are transitions from each vertex for each input letter. In our examples, the Mile machine gun is complete , and the Moore machine gun is partial .
And again: If there are more arcs from one vertex than the input letters (that is, 2 or more arcs with the same input letters), then such an automaton is called non-deterministic . This can happen when building a formalized description and then it will be necessary to make a transition to a deterministic automaton, but this is not always possible. I also omit the description of this process, immediately drawing a deterministic automaton.
That's all about the graphs.
The graphs are clearer for a person, and the tables for a car. Any automaton can be represented as a table of transitions and exits (SATs). In the SAT, the lines are the internal states of the automaton, and the columns are the input letters.
Construct TPV for our graphs Mile and Moore. If no input or output letter is defined, then a dash is put instead. If the state is not defined, then the same simple rule applies.
In TPV Miles, transitions and exits are recorded in each cell. For example, if the machine is in the C0 state and the letter a1 arrives at the input, it will go to the C1 state and the letter b3 will appear at the output.
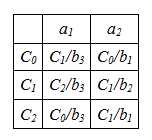
For graph Moore build the marked transition table. An additional column is selected for output letters.
In the cell under the input letter is written in what state the machine goes, in the extreme right cell - which output letter returns.
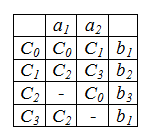
With the help of abstract automata, almost anything can be described. You can describe the operation of the digital circuit, and you can - a syntax or lexical analyzer. Let's try to describe the trigger - what is not automatic?
To set the graph you need a verbal description of the trigger operation algorithm. We read:
Encode the input and output alphabets:
A = {a0, a1}, where a0 is a logical 1 at the input of R, a1 is a logical unit at the input of S.
B = {b0, b1}, where b0 is a logical 0 at the output of Q, b1 is a logical unit at the output of Q.
Build a graph automaton Miles:

Here is such a funny cheburashka turned out :-). Now you can build a table of transitions and exits:

If we paint this table by transforming the legend into actual, then we get a table which is a trigger transition table. Then it can be simplified:
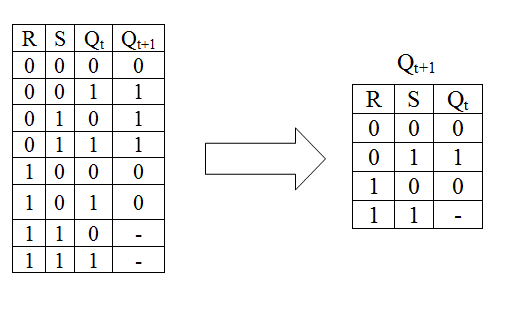
Put the obtained function on the map of Veitch and minimize:
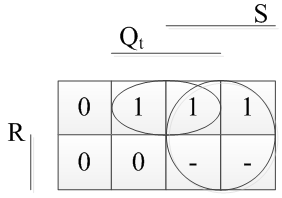
We write out what happened:

We build the scheme according to the function (Did you do your homework?):
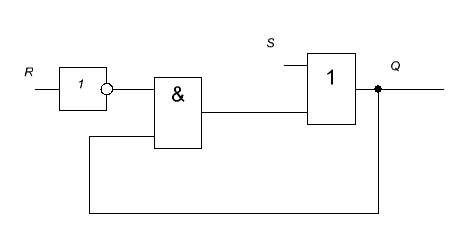
It is a bit unusual to see a trigger in a boolean basis, so we translate the function into the AND-NOT basis and draw a diagram in it:
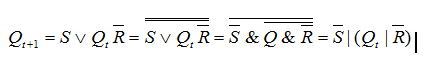

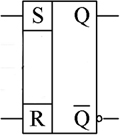
And on the asynchronous RS trigger scheme is indicated like this:
Now, if you make a little effort, you can independently synthesize a simple Christmas garland.
In the previous article I tried to set out all the basic definitions and principles in order to make this article as clear as possible. Everything did not fit, so I strongly advise you to read these files:
Basis , Basis2 , Minimization . Later in this article I left a few explanatory notes in italics.
In this article I will try to explain in accessible language what an abstract automaton is, how to present it. Since automata theory is full of mathematics and complex, I will try to write in human language so that an unprepared reader can understand what is being said.

Electronic digital circuits can be formally divided into 2 classes:
- Combination Schemes (CS) - do not have memory. The output signal is formed depending on the combination of input data at a fixed point in time (taking into account the delay in signal conversion). Combination schemes, their types and construction principles can be a topic for a separate article, and you can give as examples: Managed buses, multiplexers and demultiplexers, decoders and encoders, code converters, combinational counters and adders, etc.
- Memory circuits - the algorithm of their operation depends on the state of the inputs and memory (what was at previous times). These schemes are described using the theory of finite automata. It is about them and will go on.
In other words, the first class is logical devices that process the input signal. The second elements have memory and react to the signal depending on the data entered into them.
')
Abstract machine
The machine will have to implement some functions that are set by the developer. It can be a simple adder, it can implement a processor micro-command, select words from the main memory, or parse an expression.
In general, without going into details, the abstract automaton can be represented as follows:

Or, if we move from an illustration to a mathematical description:
A = <A, B, C, δ, λ>
Legend:
- The set {A} - is the set of values at the physical inputs of the automaton. In our case, there will be some sequence of high and low voltage levels that will encode logical zeros and ones.
- The set {B} - is the set of values at the physical outputs of the automaton.
- The set {C} is a set that represents the internal state of the automaton — memory. For the future, C0 will denote the initial state of the automaton.
- δ = X × Z → Z are the transition functions of the automaton, they uniquely determine the state ai to which the automaton passes from the state aj.
- λ = X × Z → Y - functions of the outputs, they determine what is at the output of the automaton depending on the inputs and the internal state.
δ and λ are not shown in the diagram for visual simplification.
Such an automaton functions discretely in time, that is, the values of the inputs, outputs, and the internal state of the automaton change at discrete points in time.
So, we have described in general terms what the Abstract Automaton is. An example of such an automaton may be a trigger, a computer register or an adder.
There are 2 types of machines:
- Automatic Miles. Described by a system of equations:
c (t) = δ (a (t), c (t-1));
b (t) = λ (a (t), c (t-1)). - Moore's machines. Described by the equations:
c (t) = δ (a (t), c (t-1));
b (t) = λ (a (t), c (t)).
As can be seen, the state of the automaton c (t) at the current time is a function of its state at the previous time and the input signal .
Automata differ by the type of exit function. In the Miles machine, the output signal is determined by the input signal a (t) and the state of the machine at the previous time instant c (t-1). The output of Moore’s automaton is determined by the pair of the input signal a (t) and the current state c (t).
It can also be noted that from one type you can go to the second and vice versa, and during the transition from the Mile to the Moore, the number of internal states of the automaton will remain the same, and during the reverse transition the number of internal states may increase. We will not dwell on this in detail, considering that we have synthesized (drew a graph) an automaton of the type that is needed.
So, on this with materiel over. Let's try to describe automata.
Those. an automatic machine of the type Miles produces an output signal when it changes its input, depending on its previous state. In this case, the duration of the output signal does not depend on the duration of the input signal, but only on its presence. In Moore type automata, the output signal depends on the state of the automaton at the current time, i. the machine will generate a certain output signal until it changes its state.
Ways of Automating
As we found out in the first part, an automaton is a set of input and output alphabets, a set of internal states and functions defining transitions and exits. However, usually the functions δ and λ are not specified, and the behavior of the automaton has to be described differently.
There are two main ways to set the machine:
- Using graphs.
- With the help of transition tables and exits.
Counts
An automaton graph is a directed connected graph whose vertices symbolize the internal states of the automaton, and arcs represent transitions from one state to another.

For the Miles graph on arcs, similar and output letters are indicated. The output letters are written over the arcs, symbolizing that the output state depends on the state of the machine at the previous time.

For the graph of Moore’s automaton, only input letters are written on arcs, while the output is indicated near the vertices.
Important point: If from each vertex there are as many arcs as there are input letters, then the automaton is called complete . In other words, if there are transitions from each vertex for each input letter. In our examples, the Mile machine gun is complete , and the Moore machine gun is partial .
And again: If there are more arcs from one vertex than the input letters (that is, 2 or more arcs with the same input letters), then such an automaton is called non-deterministic . This can happen when building a formalized description and then it will be necessary to make a transition to a deterministic automaton, but this is not always possible. I also omit the description of this process, immediately drawing a deterministic automaton.
That's all about the graphs.
Conversion tables and outputs.
The graphs are clearer for a person, and the tables for a car. Any automaton can be represented as a table of transitions and exits (SATs). In the SAT, the lines are the internal states of the automaton, and the columns are the input letters.
Construct TPV for our graphs Mile and Moore. If no input or output letter is defined, then a dash is put instead. If the state is not defined, then the same simple rule applies.
TPV Count Miles
In TPV Miles, transitions and exits are recorded in each cell. For example, if the machine is in the C0 state and the letter a1 arrives at the input, it will go to the C1 state and the letter b3 will appear at the output.
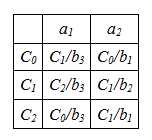
TPV Count Moore
For graph Moore build the marked transition table. An additional column is selected for output letters.
In the cell under the input letter is written in what state the machine goes, in the extreme right cell - which output letter returns.
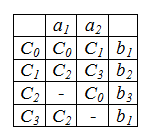
An example of the synthesis of the machine
With the help of abstract automata, almost anything can be described. You can describe the operation of the digital circuit, and you can - a syntax or lexical analyzer. Let's try to describe the trigger - what is not automatic?
To set the graph you need a verbal description of the trigger operation algorithm. We read:
Encode the input and output alphabets:
A = {a0, a1}, where a0 is a logical 1 at the input of R, a1 is a logical unit at the input of S.
B = {b0, b1}, where b0 is a logical 0 at the output of Q, b1 is a logical unit at the output of Q.
Build a graph automaton Miles:

Here is such a funny cheburashka turned out :-). Now you can build a table of transitions and exits:

If we paint this table by transforming the legend into actual, then we get a table which is a trigger transition table. Then it can be simplified:

Put the obtained function on the map of Veitch and minimize:

We write out what happened:

We build the scheme according to the function (Did you do your homework?):

It is a bit unusual to see a trigger in a boolean basis, so we translate the function into the AND-NOT basis and draw a diagram in it:
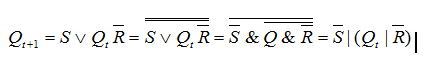

And on the asynchronous RS trigger scheme is indicated like this:

Now, if you make a little effort, you can independently synthesize a simple Christmas garland.
Source: https://habr.com/ru/post/91968/
All Articles