Pearls of functional programming: drawing trees
In this article, I'm going to tell readers about drawing trees. No, not those trees that grow from the soil and in which squirrels live. Today we will visualize trees as data structures. This article is based on the Andrew Kennedy "Functional Pearls: Drawing Trees" article from the Journal of Functional Programming, 6 (3): 527-534, Cambridge University Press, May 1996 (electronic version of the article here ), and is, in a way its translation.
The original article is written in English and uses the implementation on Standart ML. Frankly, I just stole everything from the above article, translated English into Russian (something in my own words), Standart ML translated into Erlang, threw something away (more), added something (less). Code samples will be given on both the original Standart ML and Erlang so that the curious reader can see the difference.
')
The article immediately interested me, and I wanted to get a ready-made program for such visualization. No, not for some useful use, but only because of the desire to get the same conclusion as in the article. Along the way, it was possible to play around with Erlang and get acquainted with the syntax of an unfamiliar Standart ML.
The essence is this: having a tree with text labels of each node, assign them a position and beautifully and aesthetically draw a tree on the screen. We agree that nodes that have the same depth in the tree are drawn on the same level, so the problem is reduced to finding the horizontal position of each node. But what does it mean aesthetically and beautifully? We list the rules that clearly define the beauty and aesthetics:
Example for rule 3:

Example for rule 4:
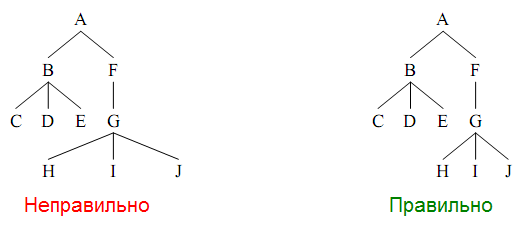
We solve the presentation problem as follows. First, we draw all the child nodes so as not to break any of the listed rules. We customize them together without changing their form (otherwise we break rule 4) so as not to break rules 1 and 3. Finally, we center the parent node relative to the child nodes and complete processing.
A critical operation is subtree fitting. Each subtree has a space — an empty zone around the tree. Since the shape of the subtrees should not change, their spaces fit as tightly as possible. Unfortunately, the final position of the subtrees in this case will depend on the order in which we make the fit. An example of two different fittings of the same spaces:

We can customize subtrees either to the left or to the right, bypassing them in the appropriate direction. In order not to violate rule 3, we will do both actions, and the result will be the arithmetic average of these two detours.
In the original, to represent the trees, the ML polymorphism is used and the data are described as follows:
This means that a node consists of a value (type 'a) and a list of child trees. In the original, the algorithm takes as input trees of the type 'a Tree and returns positioned trees of the type (' a * real) Tree. Here the second element stores the horizontal position of the node relative to the parent node . Since I don’t know anything about polymorphism in Erlang, there’s only one data type for the node, and it already contains a horizontal position:
Since we decided to use the relative position of the node, the node offset operation can be performed in constant time:
The tree space is represented by a list of pairs on ML and just a pair on Erlang:
The components of the pairs, respectively, contain the left and right borders of the space. The first pair in the list corresponds to the root of the tree. It is important to mention that, unlike the tree view, the positions of the space are absolute .
The function for horizontal space movement will look like this:
In the version on Erlang, the reader probably noticed a strange use of tuples in the function arguments. This style will be used in many of the following functions to provide easy lists: zip .
We also need to combine two non-intersecting spaces, filling the hole between them. This is done by taking the coordinates of the left position of the first space and the coordinates of the right position of the second space:
The author of the original article draws our attention to how lists of spaces of different depth are processed. On Erlang, it looks like this:
This operation can be extended to the list of spaces as follows:
From myself I ask you to pay special, close attention to the version on Erlang. Two arguments are passed to the first convolution argument, the lamba function: Elem, Acc. However, in merge_extent they are transmitted in reverse order: Acc, Elem. When I distorted the code on Erlang, I didn’t notice it because of inattention, and I made the same order. As a result, the union of spaces worked in some places incorrectly, and the conclusion was crooked in some parts of the tree.
To better understand the cause of the malfunction, consider what happens if the input to this function (the wrong version):
The following values are given:
When the arguments to merge_extent were passed in the same order as to the input of the lyamb, I observed the following debugging output:
As you can see, we got a strange space {extent, 80, -73}, where the left border is to the right of the right. The reason is easy to see if you look at the function merge_extent. However, if you don’t touch the order of the arguments, then this “wrong” version can be made correct by replacing the left convolution with the right one: replacing foldl with foldr.
Strange, but the author notes in his article below that: “We could have used the left associative convolution because the merge function is associative”. Maybe I did not understand something, but in my opinion this is a lie and a provocation. Please correct me if I missed something.
An example of using the function merge_extent_list is shown in the figure:

To begin with, we will write a function that determines how close two trees can be to each other. The function takes two spaces as input and returns the minimum possible distance between nodes:
In the original article, the minimum distance is 1.0, and I used a constant:
Now we expand this function to the list of spaces. We will calculate positions for each of them assuming that the leftmost one has a zero position. The function works by accumulating the resulting space, alternately fitting it to the next space. The result of the function is asymmetric, since the list is traversed from left to right .
The opposite effect is obtained in the following function, which calculates the position relative to the rightmost space, whose position is zero. Here rev is a reversal of the list, and ~ is a sign negation.
However, the latter function can be implemented differently. fitlistr can be defined through fitlistl using composition functions.
Finally, in order to achieve symmetry in the tree display, we calculate the positions in both ways and take the average of their results.
Now it's time to put all the components together and write a function that takes as input a tree with labels in the nodes and produces the same tree, but with coordinates for each node. The root of the tree has a zero position.
Here's how it works: first, all trees are recursively composed. The result is a list of pairs (tree, extent) to which we apply unzip and get two lists. The roots of all subtrees have a zero position. Next, we flush the space with the fillist (fit_extent_list) function, getting a list of offsets in the positions. Then we shift each subtree in trees to the corresponding offset from positions and get ptrees. Do the same for spaces and get pextents. In conclusion, we calculate the resulting space and the tree with the root in zero position.
The complexity of the presented algorithm is O (n²) in the worst case, where n is the number of nodes in the tree. Fortunately, you can rewrite the program to achieve linear complexity, but with some loss of code clarity. Inefficiency results from the representation of spaces. Moving a tree requires constant time due to the relativity of coordinates, and moving space has linear complexity due to the use of absolute coordinates. Using relative coordinates will reduce the complexity of the mergelist (merge_extent_list) from quadratic to linear. Unfortunately, the fit (fit_extent) and merge (merge_extent) functions will become less elegant.
In the original article, the graphical representation of the tree suddenly appears without any code generating it. Therefore, on my own, I will add an example of such a code on Erlang.
In this function, the connecting lines between nodes are drawn first, then the text of the labels of the nodes, and finally, the operation is repeated on each of the child nodes.
For completeness, here is the code that creates the test tree:
Here is what the author of the article did:
That's what happened with me:

I really wanted to write in the labels of nodes not one character, but a word. Fortunately, this is easily solved. In the design_tree function, it is necessary to correct the creation of spaces, taking into account the width of the text of the node label: the second argument to make_extent (0, 0) is replaced with something from the real world. Since I did not find the functions to get the width of the text in gs, it was decided to do it in a simple way: multiply the number of letters in the label by a certain factor. To do this, we introduce the function:
And we will use this function when getting the result tree. design_tree will look like:
We are testing. For input tree:
I got:

Personally, I like the ML code more than what I got. The code of the author of the article is more elegant, elegant and much more declarative, but the latter is rather related to the possibilities of the language.
I don’t have the full code of the author’s program, therefore I cite only my own (copy here ):
The original article is written in English and uses the implementation on Standart ML. Frankly, I just stole everything from the above article, translated English into Russian (something in my own words), Standart ML translated into Erlang, threw something away (more), added something (less). Code samples will be given on both the original Standart ML and Erlang so that the curious reader can see the difference.
Why do you need it
')
The article immediately interested me, and I wanted to get a ready-made program for such visualization. No, not for some useful use, but only because of the desire to get the same conclusion as in the article. Along the way, it was possible to play around with Erlang and get acquainted with the syntax of an unfamiliar Standart ML.
Problem and solution
The essence is this: having a tree with text labels of each node, assign them a position and beautifully and aesthetically draw a tree on the screen. We agree that nodes that have the same depth in the tree are drawn on the same level, so the problem is reduced to finding the horizontal position of each node. But what does it mean aesthetically and beautifully? We list the rules that clearly define the beauty and aesthetics:
- Two nodes that are on the same level should be located at least at a certain, given distance from each other.
- The parent node must be centered relative to the child nodes.
- Drawing a tree should be symmetrical and should take into account the reflection - the tree and the mirror reflection of its nodes should generate images that are reflections of each other.
- Identical trees should be drawn the same way - the positions of the nodes in the larger tree should not affect how they are drawn.
Example for rule 3:

Example for rule 4:

We solve the presentation problem as follows. First, we draw all the child nodes so as not to break any of the listed rules. We customize them together without changing their form (otherwise we break rule 4) so as not to break rules 1 and 3. Finally, we center the parent node relative to the child nodes and complete processing.
A critical operation is subtree fitting. Each subtree has a space — an empty zone around the tree. Since the shape of the subtrees should not change, their spaces fit as tightly as possible. Unfortunately, the final position of the subtrees in this case will depend on the order in which we make the fit. An example of two different fittings of the same spaces:

We can customize subtrees either to the left or to the right, bypassing them in the appropriate direction. In order not to violate rule 3, we will do both actions, and the result will be the arithmetic average of these two detours.
Tree view
In the original, to represent the trees, the ML polymorphism is used and the data are described as follows:
datatype 'a Tree = Node of' a * ('a Tree list)
This means that a node consists of a value (type 'a) and a list of child trees. In the original, the algorithm takes as input trees of the type 'a Tree and returns positioned trees of the type (' a * real) Tree. Here the second element stores the horizontal position of the node relative to the parent node . Since I don’t know anything about polymorphism in Erlang, there’s only one data type for the node, and it already contains a horizontal position:
-record (pnode, {label = "LABEL", pos = 0, children = []}).
Since we decided to use the relative position of the node, the node offset operation can be performed in constant time:
fun movetree (Node ((label, x), subtrees), x ': real) =
Node ((label, x + x '), subtrees)
move_ptree ({[], _X}) -> [];
move_ptree ({# pnode {pos = Pos} = Node, X}) ->
Node # pnode {pos = Pos + X}.
Space representation
The tree space is represented by a list of pairs on ML and just a pair on Erlang:
type Extent = (real * real) list
-record (extent, {left, right}).
The components of the pairs, respectively, contain the left and right borders of the space. The first pair in the list corresponds to the root of the tree. It is important to mention that, unlike the tree view, the positions of the space are absolute .
The function for horizontal space movement will look like this:
fun moveextent (e: Extent, x) = map (fn (p, q) => (p + x, q + x)) e
move_extent ({# extent {left = Left, right = Right} = Extent, Offset}) ->
Extent # extent {left = Left + Offset, right = Right + Offset};
move_extent ({ExtentList, Offset}) ->
lists: map (fun (Extent) -> move_extent ({Extent, Offset}) end, ExtentList).
In the version on Erlang, the reader probably noticed a strange use of tuples in the function arguments. This style will be used in many of the following functions to provide easy lists: zip .
We also need to combine two non-intersecting spaces, filling the hole between them. This is done by taking the coordinates of the left position of the first space and the coordinates of the right position of the second space:
fun merge ([], qs) = qs
| merge (ps, []) = ps
| merge ((p, _) :: ps, (_, q) :: qs) = (p, q) :: merge (ps, qs)
The author of the original article draws our attention to how lists of spaces of different depth are processed. On Erlang, it looks like this:
merge_extent ({# extent {left = Left}, #extent {right = Right}}) ->
#extent {left = Left, right = Right};
merge_extent ({[], []}) -> [];
merge_extent ({[], Extent}) -> Extent;
merge_extent ({Extent, []}) -> Extent;
merge_extent ({[Left | LeftRest], [Right | RightRest]}) ->
[merge_extent ({Left, Right}) | merge_extent ({LeftRest, RightRest})].
This operation can be extended to the list of spaces as follows:
fun mergelist es = fold merge es []
merge_extent_list (ExtentList) ->
lists: foldl (fun (Elem, Acc) -> merge_extent ({Acc, Elem}) end, [], ExtentList).
From myself I ask you to pay special, close attention to the version on Erlang. Two arguments are passed to the first convolution argument, the lamba function: Elem, Acc. However, in merge_extent they are transmitted in reverse order: Acc, Elem. When I distorted the code on Erlang, I didn’t notice it because of inattention, and I made the same order. As a result, the union of spaces worked in some places incorrectly, and the conclusion was crooked in some parts of the tree.
To better understand the cause of the malfunction, consider what happens if the input to this function (the wrong version):
merge_extent_list (ExtentList) ->
lists: foldl (fun (Elem, Acc) -> merge_extent ({Elem, Acc}) end, [], ExtentList).
The following values are given:
[[{extent, -80, -73}],
[{extent, -48, -41}],
[{extent, -16, -9}],
[{extent, 16,23}],
[{extent, 48.55}],
[{extent, 80.87}]]
When the arguments to merge_extent were passed in the same order as to the input of the lyamb, I observed the following debugging output:
merge_extent: Ex1: {extent, -48, -41}, Ex2: {extent, -80, -73}
merge_extent: Result: {extent, -48, -73}
merge_extent: Ex1: {extent, -16, -9}, Ex2: {extent, -48, -73}
merge_extent: Result: {extent, -16, -73}
merge_extent: Ex1: {extent, 16,23}, Ex2: {extent, -16, -73}
merge_extent: Result: {extent, 16, -73}
merge_extent: Ex1: {extent, 48.55}, Ex2: {extent, 16, -73}
merge_extent: Result: {extent, 48, -73}
merge_extent: Ex1: {extent, 80,87}, Ex2: {extent, 48, -73}
merge_extent: Result: {extent, 80, -73}
merge_extent_list: Result: [{extent, 80, -73}]
As you can see, we got a strange space {extent, 80, -73}, where the left border is to the right of the right. The reason is easy to see if you look at the function merge_extent. However, if you don’t touch the order of the arguments, then this “wrong” version can be made correct by replacing the left convolution with the right one: replacing foldl with foldr.
Strange, but the author notes in his article below that: “We could have used the left associative convolution because the merge function is associative”. Maybe I did not understand something, but in my opinion this is a lie and a provocation. Please correct me if I missed something.
An example of using the function merge_extent_list is shown in the figure:

Fitting spaces
To begin with, we will write a function that determines how close two trees can be to each other. The function takes two spaces as input and returns the minimum possible distance between nodes:
fun rmax (p: real, q: real) = if p> q then p else q fun fit ((_, p) :: ps) ((q, _) :: qs) = rmax (fit ps qs, p - q + 1.0) | fit _ _ = 0.0
fit_extent ({# extent {right = Right}, #extent {left = Left}}) ->
Right - Left +? EXTENT_SEPARATOR;
fit_extent ({[], []}) ->
0;
fit_extent ({[First | FirstRest], [Second | SecondRest]}) ->
erlang: max (fit_extent ({First, Second}), fit_extent ({FirstRest, SecondRest}));
fit_extent ({_ A, _B}) ->
0
In the original article, the minimum distance is 1.0, and I used a constant:
-define (EXTENT_SEPARATOR, 15).
Now we expand this function to the list of spaces. We will calculate positions for each of them assuming that the leftmost one has a zero position. The function works by accumulating the resulting space, alternately fitting it to the next space. The result of the function is asymmetric, since the list is traversed from left to right .
fun fitlistl es =
let
fun fitlistl 'acc [] = []
| fitlistl 'acc (e :: es) =
let val x = fit acc e
in
x :: fitlistl '(merge (acc, moveextent (e, x))) es
end
in
fitlistl '[] es
end
fit_extent_list_l (ExtentList) ->
fit_extent_list_l ([], ExtentList).
fit_extent_list_l (_Acc, []) -> [];
fit_extent_list_l (Acc, [Extent | Rest]) ->
X = fit_extent ({Acc, Extent}),
[X | fit_extent_list_l (merge_extent ({Acc, move_extent ({Extent, X})}), Rest)].
The opposite effect is obtained in the following function, which calculates the position relative to the rightmost space, whose position is zero. Here rev is a reversal of the list, and ~ is a sign negation.
fun fitlistr es =
let
fun fitlistr 'acc [] = []
| fitlistr 'acc (e :: es) =
let val x = ~ (fit e acc)
in
x :: fitlistr '(merge (moveextent (e, x), acc)) es
end
in
rev (fitlistr '[] (rev es))
end
fit_extent_list_r (ExtentList) ->
lists: reverse (fit_extent_list_r ([], lists: reverse (ExtentList))).
fit_extent_list_r (_Acc, []) -> [];
fit_extent_list_r (Acc, [Extent | Rest]) ->
X = - fit_extent ({Extent, Acc}),
[X | fit_extent_list_r (merge_extent ({move_extent ({Extent, X}), Acc}), Rest)].
However, the latter function can be implemented differently. fitlistr can be defined through fitlistl using composition functions.
val flipextent: Extent -> Extent = map (fn (p, q) => (~ q, ~ p)) val fitlistr = rev o map ~ o fitlistl o map flipextent o rev
flip_extent (#extent {left = Left, right = Right} = Extent) ->
Extent # extent {left = -Right, right = -Left};
flip_extent (ExtentList) ->
[flip_extent (Extent) || Extent <- ExtentList].
fit_extent_list_r (ExtentList) ->
lists: reverse (
[-X || X <- fit_extent_list_l (
lists: map (
fun flip_extent / 1,
lists: reverse (ExtentList)
)
)]
).
Finally, in order to achieve symmetry in the tree display, we calculate the positions in both ways and take the average of their results.
fun mean (x, y) = (x + y) /2.0 fun fitlist es = map mean (zip (fitlistl es, fitlistr es))
mean ({x, y}) ->
trunc ((X + Y) / 2).
fit_extent_list (ExtentList) ->
lists: map (
fun mean / 1,
lists: zip (fit_extent_list_l (ExtentList), fit_extent_list_r (ExtentList))
).
Making wood
Now it's time to put all the components together and write a function that takes as input a tree with labels in the nodes and produces the same tree, but with coordinates for each node. The root of the tree has a zero position.
fun design tree =
let
fun design '(Node (label, subtrees)) =
let
val (trees, extents) = unzip (map design 'subtrees)
val positions = fitlist extents
val ptrees = map movetree (zip (trees, positions))
val pextents = map moveextent (zip (extents, positions))
val resultextent = (0.0, 0.0) :: mergelist pextents
val resulttree = Node ((label, 0.0), ptrees)
in
(resulttree, resultextent)
end
in
fst (design 'tree)
end
design_tree (#pnode {label = Label, children = []}) ->
{make_pnode (Label, 0, []), [make_extent (0, 0)]};
design_tree (#pnode {label = Label, children = Children} = Node) ->
{Trees, Extents} = lists: unzip (lists: map (fun design_tree / 1, Children)),
Positions = fit_extent_list (Extents),
PTrees = lists: map (fun move_ptree / 1, lists: zip (Trees, Positions)),
PExtents = lists: map (fun move_extent / 1, lists: zip (Extents, Positions)),
ResultExtent = [make_extent (0, 0) | merge_extent_list (PExtents)],
ResultTree = Node # pnode {pos = 0, children = PTrees},
{ResultTree, ResultExtent}.
Here's how it works: first, all trees are recursively composed. The result is a list of pairs (tree, extent) to which we apply unzip and get two lists. The roots of all subtrees have a zero position. Next, we flush the space with the fillist (fit_extent_list) function, getting a list of offsets in the positions. Then we shift each subtree in trees to the corresponding offset from positions and get ptrees. Do the same for spaces and get pextents. In conclusion, we calculate the resulting space and the tree with the root in zero position.
Algorithmic complexity
The complexity of the presented algorithm is O (n²) in the worst case, where n is the number of nodes in the tree. Fortunately, you can rewrite the program to achieve linear complexity, but with some loss of code clarity. Inefficiency results from the representation of spaces. Moving a tree requires constant time due to the relativity of coordinates, and moving space has linear complexity due to the use of absolute coordinates. Using relative coordinates will reduce the complexity of the mergelist (merge_extent_list) from quadratic to linear. Unfortunately, the fit (fit_extent) and merge (merge_extent) functions will become less elegant.
Tree drawing
In the original article, the graphical representation of the tree suddenly appears without any code generating it. Therefore, on my own, I will add an example of such a code on Erlang.
-define (LAYER_HEIGHT, 30).
-define (LINE_Y_OFFSET, 10).
-define (LINE_X_OFFSET, 3).
-define (LINE_VERTICAL_LENGTH, 7).
draw_designed_tree (Canvas, X, Y,
#pnode {label = Label, pos = Pos, children = Children}) ->
NewX = X +? LINE_X_OFFSET,
NewY = Y -? LINE_Y_OFFSET,
gs: line (Canvas, [{{fs, [
{NewX, NewY -? LINE_VERTICAL_LENGTH},
{NewX, NewY},
{NewX + Pos, NewY},
{NewX + Pos, NewY +? LINE_VERTICAL_LENGTH}
]}])
gs: text (Canvas, [
{coords, [{X + Pos, Y}]},
{text, Label}
])
lists: map (
fun (Node) ->
draw_designed_tree (Canvas, X + Pos, Y +? LAYER_HEIGHT, Node)
end,
Children),
ok.
In this function, the connecting lines between nodes are drawn first, then the text of the labels of the nodes, and finally, the operation is repeated on each of the child nodes.
Creating a test tree
For completeness, here is the code that creates the test tree:
Tree = add_pnodes (
add_pnode (
make_pnode ("@"),
add_pnodes (
make_pnode ("B"),
[make_pnode ("C"),
add_pnodes (
make_pnode ("D"),
[make_pnode ("1"),
make_pnode ("2")]
),
make_pnode ("E"),
add_pnodes (
make_pnode ("F"),
[make_pnode ("1"),
make_pnode ("2"),
make_pnode ("3"),
make_pnode ("4"),
make_pnode ("5"),
make_pnode ("6")]
),
add_pnodes (
make_pnode ("G"),
[make_pnode ("1"),
make_pnode ("2"),
make_pnode ("3"),
make_pnode ("4"),
make_pnode ("5")]
),
make_pnode ("H"),
make_pnode ("I"),
make_pnode ("J")]
)
),
[add_pnodes (
make_pnode ("K"),
[make_pnode ("L"),
make_pnode ("M"),
make_pnode ("N"),
make_pnode ("O"),
make_pnode ("P")]
),
make_pnode ("Q"),
make_pnode ("R"),
make_pnode ("S"),
make_pnode ("T")]
),
Graphic output
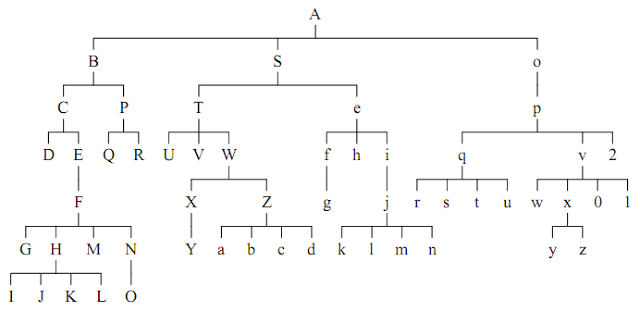
Here is what the author of the article did:

That's what happened with me:

File debugging
I really wanted to write in the labels of nodes not one character, but a word. Fortunately, this is easily solved. In the design_tree function, it is necessary to correct the creation of spaces, taking into account the width of the text of the node label: the second argument to make_extent (0, 0) is replaced with something from the real world. Since I did not find the functions to get the width of the text in gs, it was decided to do it in a simple way: multiply the number of letters in the label by a certain factor. To do this, we introduce the function:
-define (LETTER_WIDTH, 7).
label_width (Label) ->
? LETTER_WIDTH * length (Label).
And we will use this function when getting the result tree. design_tree will look like:
design_tree (#pnode {label = Label, children = []}) ->
{make_pnode (Label, 0, []), [make_extent (0, label_width (Label))]};
design_tree (#pnode {label = Label, children = Children} = Node) ->
{Trees, Extents} = lists: unzip (lists: map (fun design_tree / 1, Children)),
Positions = fit_extent_list (Extents),
PTrees = lists: map (fun move_ptree / 1, lists: zip (Trees, Positions)),
PExtents = lists: map (fun move_extent / 1, lists: zip (Extents, Positions)),
ResultExtent = [make_extent (0, label_width (Label)) | merge_extent_list (PExtents)],
ResultTree = Node # pnode {pos = 0, children = PTrees},
{ResultTree, ResultExtent}.
We are testing. For input tree:
Tree = add_pnodes (
add_pnode (
make_pnode ("@"),
add_pnodes (
make_pnode ("Beta"),
[make_pnode ("Code"),
add_pnodes (
make_pnode ("Dad"),
[make_pnode ("1st"),
make_pnode ("2dn")]
),
make_pnode ("Exit"),
add_pnodes (
make_pnode ("Fall"),
[make_pnode ("111"),
make_pnode ("222"),
make_pnode ("333"),
make_pnode ("444"),
make_pnode ("555"),
make_pnode ("666")]
),
add_pnodes (
make_pnode ("Gravity"),
[make_pnode ("1_milk"),
make_pnode ("2_apple"),
make_pnode ("3_juice"),
make_pnode ("4_banana"),
make_pnode ("5_orange")]
),
make_pnode ("Hope"),
make_pnode ("Illness"),
make_pnode ("joke")]
)
),
[add_pnodes (
make_pnode ("Kernel"),
[make_pnode ("Load"),
make_pnode ("Module"),
make_pnode ("nop"),
make_pnode ("Operator"),
make_pnode ("Point")]
),
make_pnode ("Quit"),
make_pnode ("Rest"),
make_pnode ("Set"),
make_pnode ("Terminate")]
),
I got:

findings
Personally, I like the ML code more than what I got. The code of the author of the article is more elegant, elegant and much more declarative, but the latter is rather related to the possibilities of the language.
Code
I don’t have the full code of the author’s program, therefore I cite only my own (copy here ):
-module (drawtree).
-compile (export_all).
-define (EXTENT_SEPARATOR, 15).
-define (LAYER_HEIGHT, 30).
-define (LINE_Y_OFFSET, 10).
-define (LINE_X_OFFSET, 3).
-define (LINE_VERTICAL_LENGTH, 7).
-define (LETTER_WIDTH, 7).
-define (TREE_POS_X, 350).
-define (TREE_POS_Y, 30).
-define (WINDOW_WIDTH, 1000).
-define (WINDOW_HEIGHT, 500).
-record (pnode, {label = "LABEL", pos = 0, children = []}).
-record (extent, {left, right}).
init () ->
S = gs: start ()
Win = gs: window (ui_main_window, S, [{width,? WINDOW_WIDTH}, {height,? WINDOW_HEIGHT}]),
gs: config (Win, {map, true}),
Canvas = gs: canvas (Win, [{x, 0}, {y, 0}, {width,? WINDOW_WIDTH}, {height,? WINDOW_HEIGHT}]),
do_drawings (Canvas),
loop ()
init: stop ().
move_ptree ({[], _X}) -> [];
move_ptree ({# pnode {pos = Pos} = Node, X}) ->
Node # pnode {pos = Pos + X}.
make_extent (Left, Right) ->
#extent {left = Left, right = Right}.
make_pnode (Label) ->
#pnode {label = Label}.
make_pnode (Label, Pos, Children) ->
#pnode {label = Label, pos = Pos, children = Children}.
add_pnode (#pnode {children = Children} = Tree, PNode) ->
Tree # pnode {children = [PNode | Children]}.
add_pnodes (#pnode {children = Children} = Tree, PNodes) ->
Tree # pnode {children = PNodes ++ Children}.
do_drawings (Canvas) ->
Tree = add_pnodes (
add_pnode (
make_pnode ("@"),
add_pnodes (
make_pnode ("Beta"),
[make_pnode ("Code"),
add_pnodes (
make_pnode ("Dad"),
[make_pnode ("1st"),
make_pnode ("2nd")]
),
make_pnode ("Exit"),
add_pnodes (
make_pnode ("Fall"),
[make_pnode ("111"),
make_pnode ("222"),
make_pnode ("333"),
make_pnode ("444"),
make_pnode ("555"),
make_pnode ("666")]
),
add_pnodes (
make_pnode ("Gravity"),
[make_pnode ("1_milk"),
make_pnode ("2_apple"),
make_pnode ("3_juice"),
make_pnode ("4_banana"),
make_pnode ("5_orange")]
),
make_pnode ("Hope"),
make_pnode ("Illness"),
make_pnode ("joke")]
)
),
[add_pnodes (
make_pnode ("Kernel"),
[make_pnode ("Load"),
make_pnode ("Module"),
make_pnode ("nop"),
make_pnode ("Operator"),
make_pnode ("Point")]
),
make_pnode ("Quit"),
make_pnode ("Rest"),
make_pnode ("Set"),
make_pnode ("Terminate")]
),
io: format ("Source = ~ p ~ n", [Tree]),
{DesignedTree, Extents} = design_tree (Tree),
io: format ("DesignedTree = ~ p ~ n", [DesignedTree]),
io: format ("Extents = ~ p ~ n", [Extents]),
draw_designed_tree (Canvas,? TREE_POS_X,? TREE_POS_Y, DesignedTree).
move_extent ({# extent {left = Left, right = Right} = Extent, Offset}) ->
Extent # extent {left = Left + Offset, right = Right + Offset};
move_extent ({ExtentList, Offset}) ->
lists: map (fun (Extent) -> move_extent ({Extent, Offset}) end, ExtentList).
merge_extent ({# extent {left = Left}, #extent {right = Right}}) ->
#extent {left = Left, right = Right};
merge_extent ({[], []}) -> [];
merge_extent ({[], Extent}) -> Extent;
merge_extent ({Extent, []}) -> Extent;
merge_extent ({[Left | LeftRest], [Right | RightRest]}) ->
[merge_extent ({Left, Right}) | merge_extent ({LeftRest, RightRest})].
merge_extent_list (ExtentList) ->
% IMPORTANT: Notice Elem and Acc change!
% fun (Elem, Acc) -> merge_extent ({Acc, Elem}
lists: foldl (fun (Elem, Acc) -> merge_extent ({Acc, Elem}) end, [], ExtentList).
fit_extent ({# extent {right = Right}, #extent {left = Left}}) ->
Right - Left +? EXTENT_SEPARATOR;
fit_extent ({[], []}) ->
0;
fit_extent ({[First | FirstRest], [Second | SecondRest]}) ->
erlang: max (fit_extent ({First, Second}), fit_extent ({FirstRest, SecondRest}));
fit_extent ({_ A, _B}) ->
0
fit_extent_list_l (ExtentList) ->
fit_extent_list_l ([], ExtentList).
fit_extent_list_l (_Acc, []) -> [];
fit_extent_list_l (Acc, [Extent | Rest]) ->
X = fit_extent ({Acc, Extent}),
[X | fit_extent_list_l (merge_extent ({Acc, move_extent ({Extent, X})}), Rest)].
flip_extent (#extent {left = Left, right = Right} = Extent) ->
Extent # extent {left = -Right, right = -Left};
flip_extent (ExtentList) ->
[flip_extent (Extent) || Extent <- ExtentList].
fit_extent_list_r (ExtentList) ->
lists: reverse (
[-X || X <- fit_extent_list_l (
lists: map (
fun flip_extent / 1,
lists: reverse (ExtentList)
)
)]
).
% fit_extent_list_r (ExtentList) ->
% lists: reverse (fit_extent_list_r ([], lists: reverse (ExtentList))).
% fit_extent_list_r (_Acc, []) -> [];
% fit_extent_list_r (Acc, [Extent | Rest]) ->
% X = - fit_extent ({Extent, Acc}),
% [X | fit_extent_list_r (merge_extent ({move_extent ({Extent, X}), Acc}), Rest)].
mean ({x, y}) ->
trunc ((X + Y) / 2).
fit_extent_list (ExtentList) ->
lists: map (
fun mean / 1,
lists: zip (fit_extent_list_l (ExtentList), fit_extent_list_r (ExtentList))
).
label_width (Label) ->
? LETTER_WIDTH * length (Label).
design_tree (#pnode {label = Label, children = []}) ->
{make_pnode (Label, 0, []), [make_extent (0, label_width (Label))]};
design_tree (#pnode {label = Label, children = Children} = Node) ->
{Trees, Extents} = lists: unzip (lists: map (fun design_tree / 1, Children)),
Positions = fit_extent_list (Extents),
PTrees = lists: map (fun move_ptree / 1, lists: zip (Trees, Positions)),
PExtents = lists: map (fun move_extent / 1, lists: zip (Extents, Positions)),
ResultExtent = [make_extent (0, label_width (Label)) | merge_extent_list (PExtents)],
ResultTree = Node # pnode {pos = 0, children = PTrees},
{ResultTree, ResultExtent}.
draw_designed_tree (Canvas, X, Y,
#pnode {label = Label, pos = Pos, children = Children}) ->
NewX = X +? LINE_X_OFFSET,
NewY = Y -? LINE_Y_OFFSET,
gs: line (Canvas, [{{fs, [
{NewX, NewY -? LINE_VERTICAL_LENGTH},
{NewX, NewY},
{NewX + Pos, NewY},
{NewX + Pos, NewY +? LINE_VERTICAL_LENGTH}
]}])
gs: text (Canvas, [
{coords, [{X + Pos, Y}]},
{text, Label}
])
lists: map (
fun (Node) ->
draw_designed_tree (Canvas, X + Pos, Y +? LAYER_HEIGHT, Node)
end,
Children),
ok.
loop () ->
receive
{gs, ui_main_window, destroy, _Data, _Args} ->
ok;
_Other ->
loop ()
end.
Source: https://habr.com/ru/post/91711/
All Articles