Scant him
Hello!
Today I want to make out another classical task for combinatorial games - a scanty one. Everyone knows that in the theory of games with a normal ending it occupies a central place, since all combinatorial games with a normal ending are reduced to it. Let's see how things are with the modification of the usual neem.
First, let us recall the formal definition of a neem, the strategy of the game and the theorems associated with it.
How to determine who will win in the optimal game of both rivals? This is what the Buton theorem tells us:
Let there be N heaps of neem, the number of pebbles in each of them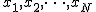
. Then the current position is losing if 
where 
- The bit modulo 2 (xor) icon. The proof of the theorem is based on the fact that from any position with a zero one-sum it is possible to go only to a position with a non-zero (except for empty piles), and from any position with a non-zero one-sum it can always go to a position with zero. After a correct sequence of moves, a player with a non-zero him-sum always wins, since after his moves he leaves zero-him sum, strictly reducing the number of stones, therefore, sooner or later it is he who will take the last stones. Let's see how this theorem works with an example, let us have three piles with the number of 3, 8, 15 stones in each. We write these numbers in a column in the binary representation and calculate xor, it is equal to zero, then the second player, let's call it Y, is in the winning position. His strategy is to leave a position with zero him-sum by any course. Consider possible moves, where Y sticks to its strategy and eventually wins:
It turns out that the strategy of the game in it is simple, it is even easier to determine the winner with the optimal strategy, now let's move on to our scanty neem task. The rules are the same with him, except for one thing: now the one who takes the last stone loses. Our task is to determine by the size of the piles who will win at the optimal strategy. This time the game is miserable, so it is not always possible to reduce it to it, we do not have clear algorithms and approaches to solve this problem, they will have to be invented from scratch. In the solution I proposed, we will try to reduce the meager one to the usual, in this case it is possible, but after some conclusions.
So, first we need to find a position that will be a winning one for a scanty neem, as well as for a normal one, for this we present the case when there are K piles of unit size and one pile on the table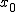
with the size of more than one stone. In the event that we play the usual him, I will take from 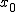the stones, leaving one or zero so that after my move the opponent got an even number of single piles, then I will win with any strategies; and if we play the meager one, then I will leave an odd number of heaps with one stone. Thus, we have found the position in which the player wins in both games. Now we divide all possible starting positions into two groups:
It is easy to see that in the first case, to give an answer, it suffices to check the parity of the number of heaps. In the case of evenness, X wins, in the case of odd Y. Now we consider the second case. You may notice that the optimal strategy here will be to reduce the game to the position indicated by us with K in single piles and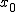 a bunch more than one size, let's call this position A. And no matter how the game passes, position A will be reached one of the players sooner or later. Whoever gets into this position will win, both in a scanty and normal, and from this it follows that we can check the starting position for winning, as if we were playing in a normal position, calculating the xor of all the piles. If xor is zero, then the second player will get to position A first, where nothing will prevent him from making a winning move in a scanty name. Otherwise, this move will get X.
Thus, breaking the game into two cases, we easily overcome our task, here is its solution written in java:
There is no general approach to scanty games, sometimes they come down to games with a normal ending, sometimes not, they just need intelligence and a little imagination)
Thanks for attention.
Today I want to make out another classical task for combinatorial games - a scanty one. Everyone knows that in the theory of games with a normal ending it occupies a central place, since all combinatorial games with a normal ending are reduced to it. Let's see how things are with the modification of the usual neem.
First, let us recall the formal definition of a neem, the strategy of the game and the theorems associated with it.
| Nim is a math game in which two players take turns taking items laid out in several piles. In one move can be taken any number of items (greater than zero) from one pile. Wins the player who took the last item. |
How to determine who will win in the optimal game of both rivals? This is what the Buton theorem tells us:
Let there be N heaps of neem, the number of pebbles in each of them
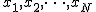. Then the current position is losing if where - The bit modulo 2 (xor) icon. The proof of the theorem is based on the fact that from any position with a zero one-sum it is possible to go only to a position with a non-zero (except for empty piles), and from any position with a non-zero one-sum it can always go to a position with zero. After a correct sequence of moves, a player with a non-zero him-sum always wins, since after his moves he leaves zero-him sum, strictly reducing the number of stones, therefore, sooner or later it is he who will take the last stones. Let's see how this theorem works with an example, let us have three piles with the number of 3, 8, 15 stones in each. We write these numbers in a column in the binary representation and calculate xor, it is equal to zero, then the second player, let's call it Y, is in the winning position. His strategy is to leave a position with zero him-sum by any course. Consider possible moves, where Y sticks to its strategy and eventually wins:It turns out that the strategy of the game in it is simple, it is even easier to determine the winner with the optimal strategy, now let's move on to our scanty neem task. The rules are the same with him, except for one thing: now the one who takes the last stone loses. Our task is to determine by the size of the piles who will win at the optimal strategy. This time the game is miserable, so it is not always possible to reduce it to it, we do not have clear algorithms and approaches to solve this problem, they will have to be invented from scratch. In the solution I proposed, we will try to reduce the meager one to the usual, in this case it is possible, but after some conclusions.
So, first we need to find a position that will be a winning one for a scanty neem, as well as for a normal one, for this we present the case when there are K piles of unit size and one pile on the table
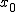with the size of more than one stone. In the event that we play the usual him, I will take from 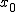the stones, leaving one or zero so that after my move the opponent got an even number of single piles, then I will win with any strategies; and if we play the meager one, then I will leave an odd number of heaps with one stone. Thus, we have found the position in which the player wins in both games. Now we divide all possible starting positions into two groups:- On the table only single handfuls
- There are heaps of two or more on the table
It is easy to see that in the first case, to give an answer, it suffices to check the parity of the number of heaps. In the case of evenness, X wins, in the case of odd Y. Now we consider the second case. You may notice that the optimal strategy here will be to reduce the game to the position indicated by us with K in single piles and
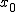a bunch more than one size, let's call this position A. And no matter how the game passes, position A will be reached one of the players sooner or later. Whoever gets into this position will win, both in a scanty and normal, and from this it follows that we can check the starting position for winning, as if we were playing in a normal position, calculating the xor of all the piles. If xor is zero, then the second player will get to position A first, where nothing will prevent him from making a winning move in a scanty name. Otherwise, this move will get X.Thus, breaking the game into two cases, we easily overcome our task, here is its solution written in java:
Copy Source | Copy HTML int n = nextInt(), K = 0 , nimSum = 0 ; for ( int i= 0 ; i<n; i++) { int size = nextInt(); if (size == 1 ) K++; nimSum ^= size; } if (n - K >= 1 ) out .println(nimSum == 0 ? 'Y' : 'X' ); else out .println((K& 1 )== 1 ? 'Y' : 'X' );
Copy Source | Copy HTML int n = nextInt(), K = 0 , nimSum = 0 ; for ( int i= 0 ; i<n; i++) { int size = nextInt(); if (size == 1 ) K++; nimSum ^= size; } if (n - K >= 1 ) out .println(nimSum == 0 ? 'Y' : 'X' ); else out .println((K& 1 )== 1 ? 'Y' : 'X' );Copy Source | Copy HTML int n = nextInt(), K = 0 , nimSum = 0 ; for ( int i= 0 ; i<n; i++) { int size = nextInt(); if (size == 1 ) K++; nimSum ^= size; } if (n - K >= 1 ) out .println(nimSum == 0 ? 'Y' : 'X' ); else out .println((K& 1 )== 1 ? 'Y' : 'X' );Copy Source | Copy HTML int n = nextInt(), K = 0 , nimSum = 0 ; for ( int i= 0 ; i<n; i++) { int size = nextInt(); if (size == 1 ) K++; nimSum ^= size; } if (n - K >= 1 ) out .println(nimSum == 0 ? 'Y' : 'X' ); else out .println((K& 1 )== 1 ? 'Y' : 'X' );Copy Source | Copy HTML int n = nextInt(), K = 0 , nimSum = 0 ; for ( int i= 0 ; i<n; i++) { int size = nextInt(); if (size == 1 ) K++; nimSum ^= size; } if (n - K >= 1 ) out .println(nimSum == 0 ? 'Y' : 'X' ); else out .println((K& 1 )== 1 ? 'Y' : 'X' );Copy Source | Copy HTML int n = nextInt(), K = 0 , nimSum = 0 ; for ( int i= 0 ; i<n; i++) { int size = nextInt(); if (size == 1 ) K++; nimSum ^= size; } if (n - K >= 1 ) out .println(nimSum == 0 ? 'Y' : 'X' ); else out .println((K& 1 )== 1 ? 'Y' : 'X' );Copy Source | Copy HTML int n = nextInt(), K = 0 , nimSum = 0 ; for ( int i= 0 ; i<n; i++) { int size = nextInt(); if (size == 1 ) K++; nimSum ^= size; } if (n - K >= 1 ) out .println(nimSum == 0 ? 'Y' : 'X' ); else out .println((K& 1 )== 1 ? 'Y' : 'X' );Copy Source | Copy HTML int n = nextInt(), K = 0 , nimSum = 0 ; for ( int i= 0 ; i<n; i++) { int size = nextInt(); if (size == 1 ) K++; nimSum ^= size; } if (n - K >= 1 ) out .println(nimSum == 0 ? 'Y' : 'X' ); else out .println((K& 1 )== 1 ? 'Y' : 'X' );Copy Source | Copy HTML int n = nextInt(), K = 0 , nimSum = 0 ; for ( int i= 0 ; i<n; i++) { int size = nextInt(); if (size == 1 ) K++; nimSum ^= size; } if (n - K >= 1 ) out .println(nimSum == 0 ? 'Y' : 'X' ); else out .println((K& 1 )== 1 ? 'Y' : 'X' );Copy Source | Copy HTML int n = nextInt(), K = 0 , nimSum = 0 ; for ( int i= 0 ; i<n; i++) { int size = nextInt(); if (size == 1 ) K++; nimSum ^= size; } if (n - K >= 1 ) out .println(nimSum == 0 ? 'Y' : 'X' ); else out .println((K& 1 )== 1 ? 'Y' : 'X' );Copy Source | Copy HTML int n = nextInt(), K = 0 , nimSum = 0 ; for ( int i= 0 ; i<n; i++) { int size = nextInt(); if (size == 1 ) K++; nimSum ^= size; } if (n - K >= 1 ) out .println(nimSum == 0 ? 'Y' : 'X' ); else out .println((K& 1 )== 1 ? 'Y' : 'X' );
There is no general approach to scanty games, sometimes they come down to games with a normal ending, sometimes not, they just need intelligence and a little imagination)
Thanks for attention.
')
Source: https://habr.com/ru/post/91272/
All Articles