Trimino
Hi,% usename%!
In this article I want to tell a little about combinatorial games and make out the decision of one of them. In life, we meet with this type of games, their formal definition is:
Today we will try to understand the essence of the approach to the simplest games, for this purpose we will consider the game “Trimino”, which consists in the following: there is a playing field of size 2 * N, N <= 800 and an infinite number of flat figures consisting of three cells (see figure ).  Two players take turns, let the first one be X, and the second Y. At each turn, the player places the figure, turning it as it pleases, to an empty seat. Overlay figures on each other can not. Loses the one who can not make a move. Our task is to determine who will win in the optimal game: X or Y.
Two players take turns, let the first one be X, and the second Y. At each turn, the player places the figure, turning it as it pleases, to an empty seat. Overlay figures on each other can not. Loses the one who can not make a move. Our task is to determine who will win in the optimal game: X or Y.
It is easy to see that our game has a normal ending (the one who cannot walk) loses and has the properties of combinatorial games, which means it can be reduced to the game “Nim”, which we will try to do. The general approach to this kind of problem is to break the big game into many typical, but smaller, for each of them, calculate nim value through the sum of the games, then find the mex (minimal exclusive) of all the partitions and compare it with zero. In case of equality, we get the P position, otherwise the N position. Everything would be trivial, but in our game there are some small difficulties that, after a little thought, you can get around. And the difficulty is this: the original field has the shape of a rectangle, but having placed the first three-player, we divide the game into two others, one of which is exactly the same, and the other is different in that one of its curve edges. Therefore, in our task nothing else remains, how to make several types of games, there will be 4 of them: I, II, III, IV. Schematically, they are depicted in the picture.
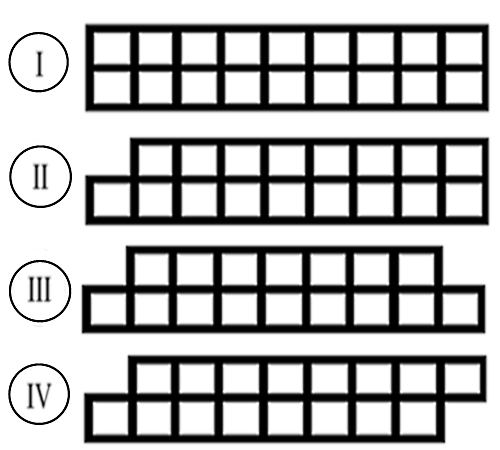
We will consider each of these types separately, placing the three-arm in any position and breaking it into the sums of other games. Now you need to follow up on which games you can break each of our types. The first type is divided into the sum of the first and second, as if we did not turn the figure, the second can be divided into two second games or the first and third. The third is divided into the second and third, the fourth also into the second and third. We consider symmetrical variants to be the same, since they are identical and will not affect mex, thus we notice that the third and fourth variants are absolutely the same, which means we can do only one of them, thereby reducing our task. The figure below shows the partitioning methods:

Taking into account the comments made and carefully arranging the triminoes, we will write three recursive functions with memorization in the java language.
Now we just have to give our answer:
In the analysis of this problem, I tried to show a common style of thinking, it is almost the same type in solving such problems. The task analyzed above is taken from the SPOJ archive and is available via the TRIOMINO link.
')
Thanks for attention.
In this article I want to tell a little about combinatorial games and make out the decision of one of them. In life, we meet with this type of games, their formal definition is:
| A combinatorial game is a set of game positions, about each of which players know how (to what other positions) each of them can go. |
 Two players take turns, let the first one be X, and the second Y. At each turn, the player places the figure, turning it as it pleases, to an empty seat. Overlay figures on each other can not. Loses the one who can not make a move. Our task is to determine who will win in the optimal game: X or Y.
Two players take turns, let the first one be X, and the second Y. At each turn, the player places the figure, turning it as it pleases, to an empty seat. Overlay figures on each other can not. Loses the one who can not make a move. Our task is to determine who will win in the optimal game: X or Y.It is easy to see that our game has a normal ending (the one who cannot walk) loses and has the properties of combinatorial games, which means it can be reduced to the game “Nim”, which we will try to do. The general approach to this kind of problem is to break the big game into many typical, but smaller, for each of them, calculate nim value through the sum of the games, then find the mex (minimal exclusive) of all the partitions and compare it with zero. In case of equality, we get the P position, otherwise the N position. Everything would be trivial, but in our game there are some small difficulties that, after a little thought, you can get around. And the difficulty is this: the original field has the shape of a rectangle, but having placed the first three-player, we divide the game into two others, one of which is exactly the same, and the other is different in that one of its curve edges. Therefore, in our task nothing else remains, how to make several types of games, there will be 4 of them: I, II, III, IV. Schematically, they are depicted in the picture.

We will consider each of these types separately, placing the three-arm in any position and breaking it into the sums of other games. Now you need to follow up on which games you can break each of our types. The first type is divided into the sum of the first and second, as if we did not turn the figure, the second can be divided into two second games or the first and third. The third is divided into the second and third, the fourth also into the second and third. We consider symmetrical variants to be the same, since they are identical and will not affect mex, thus we notice that the third and fourth variants are absolutely the same, which means we can do only one of them, thereby reducing our task. The figure below shows the partitioning methods:

Taking into account the comments made and carefully arranging the triminoes, we will write three recursive functions with memorization in the java language.
Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }
Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }Copy Source | Copy HTML private static int M = 800 ; private static int [] I = new int [M+ 1 ], II = new int [M+ 1 ],III = new int [M+ 1 ]; static { Arrays.fill(I, - 1 ); Arrays.fill(II, - 1 ); Arrays.fill(III, - 1 ); } private static int I( int n) { if (I[n] >= 0 ) return I[n]; if (n == 0 || n == 1 ) return I[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 1 ; i<n; i++) mex[I(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return I[n] = i; return I[n] = M+1 ; } private static int II( int n) { if (II[n] >= 0 ) return II[n]; if (n == 0 || n == 1 ) return II[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[II(i - 1 ) ^ II(n - i)] = true ; for ( int i= 2 ; i<=n; i++) mex[III(i - 1 ) ^ I(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return II[n] = i; return II[n] = M+1 ; } private static int III( int n) { if (III[n] >= 0 ) return III[n]; if (n == 0 || n == 1 ) return III[n] = 0 ; boolean [] mex = new boolean [M+ 1 ]; for ( int i= 2 ; i<n; i++) mex[III(i - 1 ) ^ II(n - i)] = true ; for ( int i= 0 ; i<=M; i++) if (!mex[i]) return III[n] = i; return III[n] = M+1 ; }
Now we just have to give our answer:
Copy Source | Copy HTML
- int n = nextInt ();
- out .println (I (n) == 0 ? 'Y' : 'X' );
In the analysis of this problem, I tried to show a common style of thinking, it is almost the same type in solving such problems. The task analyzed above is taken from the SPOJ archive and is available via the TRIOMINO link.
')
Thanks for attention.
Source: https://habr.com/ru/post/91242/
All Articles