Review of neural network evolution methods

The choice of topology and adjustment of the weights of artificial neural network (ANN) connections are one of the most important steps when using neural network technologies to solve practical problems. The quality (adequacy) of the obtained neural network model, control system, etc. directly depends on these stages.

The construction of an artificial neural network by the traditional method is performed, in fact, by trial and error. The researcher sets the number of layers, neurons, as well as the structure of connections between them (presence / absence of recurrent connections), and then looks at what happened - the network is trained using some method, and then tested on a test sample. If the results of the work meet the specified criteria, the task of building the INS is considered completed successfully; otherwise, the process is repeated with different values ​​of the original parameters.
')
Naturally, the rapid development of the theory and practice of using genetic algorithms made researchers (laziness - the engine of progress) look for ways to apply them to the task of finding the optimal structure of an ANN (evolution of neural networks or neuroevolution), especially since, so to speak, proof-of-concept there was, or, more precisely, in the head - nature clearly demonstrated the solvability of a similar problem on the example of the evolution of the nervous system with the subsequent formation and development of the brain.


UPD: Thanks for the karma :) Moved to Artificial Intelligence.
UPD2: Redid end links

First a couple of words about authorship. Most of the descriptive text is taken from the article by Anton Konushin [1]. Additionally, the materials listed at the end of the article were used (the relevant references are provided during the presentation), as well as the results of my own research.

Next, I will proceed from the assumption that the reader is familiar with the concepts of ANNs and genetic algorithms, and omit their description. Those who want to know - yes, google or refer to the list of sources at the end of the article. So let's go.

Coding Schemes

As most researchers note, the central point of any method for the evolution of neural networks is the choice of a genetic representation (i.e., a coding scheme and appropriate decoding). The choice of representation determines the class of networks that can be built using this method. In addition, the effectiveness of the method in all parameters depends on them.

The general properties of genetic representations, by which one can evaluate and compare various methods, have been distinguished by many authors. Balakrishnan and Honavan [2] suggest using the following set of properties: completeness, isolation, compactness, scalability, multiplicity, ontogenetic adaptability, modularity, redundancy complexity.
In this article I will not dwell on this list in more detail. A brief description of these properties can be found in [1], and a more detailed - in [2]

At present, there are usually two large classes of encoding methods: direct encoding and indirect encoding.

The use of the terms “parametric” and “indirect” coding to refer to this class of methods is also found in the Russian-language literature. Personally, such a translation seems to me not very good, so here and further I will use the term “indirect”

Direct coding operates on chromosomes representing a linear representation of the ANN, in which all neurons, ANN weights and connections are explicitly indicated. Thus, it is always possible to build a one-to-one correspondence between the structural elements of the ANN (neurons, connections, weights, etc.), i.e. phenotype, and the corresponding parts of the chromosome, i.e. genotype.

This way of presenting the neural network is the most simple and intuitive, and also allows you to apply to the chromosomes already existing apparatus of genetic search (for example, crossing-over and mutation operators). Among the most obvious drawbacks of such a coding scheme, the “swelling” of the genotype with increasing number of neurons and ANN connections can be noted and, as a result, low efficiency due to a significant increase in search space.

For the sake of fairness, it is worth saying that techniques have been proposed for direct coding, the purpose of which is to alleviate the drawbacks described above (for example, NEAT — described below)

Indirect coding (some sources also use the term weak - weak, meaning loosely coupled) professes a more “biological” principle - the genotype does not encode the phenotype itself, but the rules for constructing it (conditionally speaking, a certain program). When decoding a genotype, these rules are applied in a certain sequence (often, recursively and, often, the applicability of the rules depends on the current context), as a result of which the neural network is built.

When using indirect coding methods, the genetic representation (and, accordingly, the search space for genetic algorithms) is more compact, and the genotype itself allows for the coding of modular structures, which, under certain conditions, gives advantages in the adaptability of the results obtained. Instead, we get the practical impossibility to trace the changes in the genotype that led to the given changes in the phenotype, as well as many difficulties with the selection of genetic operators, convergence and performance.

Historically, direct coding has been investigated earlier and deeper, but a number of drawbacks of this approach (see, for example, [4]) force researchers to look more closely at indirect coding methods. However, inherently indirect methods are very difficult to analyze. For example, the same mutation of the rule located at the beginning of the “program” has a tremendous effect, and applied to the “terminal” rules does not have any effect at all, and as a result the genetic search has a strong tendency to premature convergence. The selection of crossover operators is also not a trivial task, since The use of standard binary operators, as a rule, leads to the frequent appearance of non-viable solutions.

From the good news it can be noted that the work in the field of developing indirect coding techniques is now in full swing, and there is room for maneuver and new discoveries - so readers eager for scientific glory have a chance to try themselves in this area.

Direct encoding

Miller, Todd and Hedge

In 1989, Miller proposed to encode the structure of a neural network using an adjacency matrix (similar to an adjacency matrix for graphs). He used it to write only multilayer neural networks without feedback. Each possible direct connection of neuron i and non-input neuron j corresponds to an element of the matrix with coordinates (i, j). If the value of this element is 1, there is a connection; if 0 - no connection. For the displacement of each neuron a separate column is allocated. Thus, a neural network of N neurons corresponds to a matrix of dimensionality N * (N + 1).

The genome of a neural network using the direct encoding method is compiled by concatenating the binary rows of the neural network adjacency matrix.

When decoding the resulting genome back into the neural network, all feedbacks (which can be recorded in the adjacency matrix) are ignored. That is why only neural networks without feedback were recorded in this form. All neurons to which no connection leads, or from which no connection exits, are deleted.

Such a representation is poorly scaled because the length of the resulting genome is proportional to the square of the number of neurons in the network. Therefore, it can be effectively used only for building sufficiently small neural networks.

This representation can also be used to build other classes of neural networks, for example, with feedback. To do this, you only need to make changes in the process of decoding the genotype.

The analysis of this direct encoding method is a non-trivial task. There are two main questions:

• What is the probability that the network will be "dead", i.e. are the inputs and outputs of the network not connected at all?
• The coding of the same network structure can be performed in a variety of ways. How to find out exactly how many of these methods exist, and how does this affect adaptation in the process of genetic search?

To answer both of these questions, it is necessary to solve complex combinatorial problems, and, as far as is known, research in this area has not been carried out [5].

Stanley, Miikkulainen

One of the most potentially successful attempts to get rid of the disadvantages of direct coding while preserving all its advantages is the method proposed in 2002 called NEAT - Neural Evolution through Augmenting Topologies [6].

In their studies, the authors identified a number of key problems inherent in direct coding in particular, and neuroevolution in general. These problems are:

• Competing Conventions - the same phenotype (topologically) ANN can be differently represented in the genotype even within the same coding method. For example - in the course of evolution between the two previously created genes (for example, A and B) the C gene was inserted, which (as is often the case with mutations) at the initial stage does not carry any useful information. As a result, we have an individual with two genes (A, B) and an individual with three genes (A, C, B). When crossing these two individuals, the crossover operator will be applied to the genes in the corresponding positions (ie, A <-> A, C <-> B), which is not very good, because we begin to cross pig (C) with oranges (B).
  
• Unprotected innovations — with neuroevolution, innovations (i.e., changes in the structure of the Ann) are made by adding or removing neurons and / or groups of neurons. And often, the addition of a new structure in the ANN leads to a decrease in the value of its fitness function. For example, adding a new neuron introduces non-linearity in a linear process, which leads to a decrease in the value of the fitness function until the weight of the added neuron is optimized.
  
• Initial size and topological innovations — in many neuroevolution techniques, the initial population is a collection of random topologies. In addition to having to spend some time sifting out initially non-viable networks (for example, those that have no input connected to any output), such populations tend to converge prematurely to solutions that are not optimal great). This is due to the fact that the initially generated random topology already has a set of links that are extremely reluctant to be reduced during the genetic search. As experiments have shown, the most effective is the search with a consistent increase in the size of the neural network - in this case, the search space is greatly narrowed. One way to solve this problem is to introduce a penalty function, which reduces the value of the fitness function depending on the size of the network. However, it remains to solve the problem of the optimal form of this function, as well as the selection of the optimal values ​​of its coefficients.
  

The solution proposed by the authors is based on the biological concept of homologous genes (alleles), as well as on the existence of a synapsis process in nature - alignment of homologous genes before the crossover.

Alleles (from the Greek. Allēlōn - each other, mutually), hereditary advances ( genes ) located in the same areas of homologous (paired) chromosomes and determine the direction of development of the same trait.

The method assumes that two genes (in two different individuals) are homologous, if they arose as a result of the same mutation in the past. In other words, for each structural mutation (gene addition), a new gene is assigned a unique number (innovation number), which then does not change in the process of evolution.

The use of historical markers (historical markings) is the basis for solving all three of the problems described above, due to:

1. Crossover runs only between homologous genes
   
2. Protection of innovation through the introduction of "niche" - individuals with similar topological structures are eliminated, thus leaving room for "beginners".
   
3. Minimization of dimensions due to consistent growth from the minimum size
   

A more detailed and complete description of the methodology, as well as its comparison with other methods, is given in [6].

Indirect coding

Kitano

In real biological organisms, the genotype is not a true complete drawing of the whole individual. It contains information about proteins, i.e. about the elements that are used both as building blocks from which an organism is created, and as mechanisms with a built-in program for building other elements of the organism. This process of development is called ontogenesis, and it was he who inspired researchers to move to the fractal descriptions of neural networks. The genotype does not record the description of the structure of the neural network, but the program and the rules for constructing this structure.

The most famous approach to the implementation of this idea is based on Lindemeir Systems, or L-systems. This formalism was originally a grammatical approach to modeling plant morphogenesis. The grammar of the L-system consists of a set of rules used to generate a string describing the structure. The process of applying the rules is called string-rewriting. Rule rewriting rules are consistently applied to the initial character S, until we get a line only from terminal characters.

In 1990, Kitano developed a graph generation grammar (Graph Generation Grammar -GGG). All rules are:



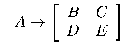
The alphabet of this grammar contains three types of characters: non-terminal N = {A, B,:, Z}, pre-terminal P = {a, b,:, p} and terminal T = {0,1}. A grammar consists of two parts: a variable and a constant. The variable part is recorded in the genome and consists of a sequence of descriptions of the rules of grammar. All characters from the left part of the rules must be non-terminal, and from the right part - from the set N? P. The constant part of the grammar contains 16 rules for each pre-terminal character on the left, and 2 * 2 matrices from {0,1} on the right. Grammar rules are also set for terminal symbols. Zero expands into a 2 * 2 matrix of zeros, and one - into the matrix and ones.

When working with such representations of genomes, situations may occur when the variable part does not specify rules for a non-terminal symbol, which, however, was used on the right-hand side of one of the described rules. Such characters are declared <dead>, and are rewritten in the same way as zeros.

The decoding process consists of sequential application of rules from the genome to the initial symbol S. The number of applications of the rules is specified at the beginning. The resulting matrix is ​​interpreted as follows: if the element (i, i) = 1 on the diagonal, then it corresponds to a neuron. All elements (i, j) denote the connection of neuron i with neuron j, if they both exist. All feedbacks are deleted.

Nolfi, Parisi

Nolfi and Parisi offered to encode neurons with their coordinates in two-dimensional space. Each pair of coordinates in the genotype corresponds to one neuron. But links are not specified exactly in the genotype, but <grown> in the decoding process. The outermost neurons on the left are considered input, and the extreme ones on the right are output.

At the beginning of the decoding process, all neurons are placed on the plane at the points specified by their coordinates. Then they are indexed. The index of hidden neurons is determined by their x coordinate. If the two x-derived coordinates of the two neurons coincide, the neuron that was read from the genome later receives a larger number (it is encoded further than the other). The indices of all input and output neurons are calculated differently. Each neuron in the genotype also corresponds to the parameter type. For input neurons, the index is I = type mod N (input), and for output neurons it is calculated using the formula j = N - N (output) + type mod N (output). Where N (input) is the number of inputs to the neural network, N (output) is the number of outputs from the neural network. Obviously, some input and output neurons will have the same index. Therefore, when decoding, N (input) input and N (output) output real neurons are added to the neural network, to which the inputs and outputs of the network are connected. Each such additional neuron is associated with all neurons with the corresponding index.

After decoding all the neurons and placing them in space, a connection tree begins to be built from each neuron. It is usually calculated as a fractal, but the specific method of its calculation is not important. The length of the segments of the branches of the tree, and the angle between the branches is set when describing each neuron in the genome. The connection between neurons is established if one of the branches of the graph approaches the other neuron less than the pre-set threshold value.

Initially, the training of networks recorded in this way was not carried out separately; they evolved along with weights, which were also recorded in the genome. But such a view can be used only to build the network structure, and weights can be calculated using standard algorithms.

Canglossi, Parisi and Nolfi

On the one hand, this method is a development of the previous one, and on the other hand, it uses a fractal generating process similar to a grammatical representation.

This approach was developed by Kangelosi, Parisi and Nolfi. Instead of encoding each neuron directly, they write a set of rules for the separation and displacement of neurons. Therefore, the method is named Generating cell space GCS.

The process of ontogenesis begins with a single cell - a special type of <egg>. This cell is then divided (<rewritten>) into two daughter cells, and the separation parameters are specified in the rule. Each of the progeny cells can be placed in one of the 8 adjacent cells. The process is repeated a specified number of times, after which all the cells constructed are <mature> and turn into neurons. They are divided into input, output and hidden by the same principle as in the previous method.

Kangelossi and Elman

This method is a more biological development of the previous one. He uses the so-called. genetic regulation network (GRN) to control the network building process. Their GRN consists of 26 regulatory elements (genes), built by analogy with biological operons. Each operon is divided into two parts - regulatory (regulatory) and expressive (expression). The regulatory part consists of two regions: an inductor and an inhibitor. The expressive part also consists of two regions: the regulatory and structural. If the regulatory region of a gene coincides with the inducer of another gene, the latter is expressed (ie, the commands specified in its structural part are executed). Expression occurs if it was not prohibited by an inhibitor of another gene. The amount of the gene expressed (“the amount of chemical elements produced”) depends on the inducer part of the regulatory element.

O'Neill and Brabazon

The method proposed by the authors is based on the formal grammar method. However, the formal grammar used to construct a sequence of commands, in turn, is described by some meta-grammar.
For example, the following universal or meta-grammar allows you to generate an arbitrary 8-bit sequence:

 <g> :: =
 "<bitstring> :: =" <reps>
 "<bbk4> :: =" <bbk4t>
 "<bbk2> :: =" <bbk2t>

 "<bbk1> :: =" <bbk1t>
 "<bit> :: =" <val>
 <bbk4t> :: = <bit> <bit> <bit> <bit>

 <bbk2t> :: = <bit> <bit>
 <bbk1t> :: = <bit>
 <reps> :: = <rept>
 |  <rept> "|"  <reps>

 <rept> :: = "<bbk4> <bbk4>"
 |  "<bbk2> <bbk2> <bbk2> <bbk2>"
 |  "<bbk1> <bbk1> <bbk1> <bbk1> <bbk1> <bbk1> <bbk1> <bbk1>"

 <bit> :: = "<bit>"
 |  one
 |  0
 <val> :: = <valt>
 |  <valt> "|"  <val>

 <valt> :: = 1 |  0

For grammar translation, an input bit string is used that indicates a sequence of rule numbers selected in cases where the non-terminal contains more than one output method.

For example, the meta grammar described above may produce the following grammar:

 <bitstring> :: = <bit> 11 <bit> 00 <bit> <bit>

 |  <bbk2> <bbk2> <bbk2> <bbk2>
 |  11011101
 |  <bbk4> <bbk4>
 |  <bbk4> <bbk4>
 <bbk4> :: = <bit> 11 <bit>

 <bbk2> :: = 11
 <bbk1> :: = 1
 <bit> :: = 1 |  0 |  0 |  one

Thus, an individual's genotype consists of two binary strings - one is designed to generate grammar based on meta-grammar, and the other is to generate, in fact, the ANN based on the resulting grammar.

For a more detailed description of the method, see [7], [8]

Other methods

There are many other methods of neuroevolution (some of which are in [5]). here I will give only brief descriptions of each of them:

• Boers and Kuiper - use context-sensitive L-systems
  
• Dilaert and Beer (Dellaert and Beer) - an approach similar to Kangelossi and Elman, but using random boolean neural networks (random boolean networks)
  
• Harp, Samad and Guha (Harp, Samad, and Guha) - Poson direct coding of structure
  
• Gruau - using a grammatical tree to specify instructions for cell division (somewhat similar to Kangelossi, Paris and Nolfi)
  
• Vaario (Vaario) - cell growth is given by L-systems
  

Comparison of different approaches to neuroevolution

Unfortunately, to unequivocally say which of the above approaches is the most optimal, is currently quite difficult. This is due to the fact that the unambiguous criterion of the "universal assessment" has not been worked out. As a rule, both the authors and third-party researchers evaluate the effectiveness on the basis of certain test problems within certain problem areas, and at the same time interpret the results very differently. Moreover, in almost all the comparative papers I have met, reservations are made about the fact that the results obtained may change when the test conditions change, and that additional research is needed (which I also make a reservation).

For reference purposes only, I present brief results of comparisons made in [5] (a number of algorithms are compared with each other) and in [6] (the NEAT method is compared with some other methods).

The following methods were compared in [5].

• Miller (direct encoding)
  
• Kitano (coding on L-systems)
  
• Nolfi (cell space)
  
• Kangelosi (generating cell space)
  

For comparison, a number of artificial and life problems were used on which the comparison was made.
Detailed results are given in [5], but in general it can be noted that:

• Kitano Evolved Nets Produce Better Results
  
• Miller's nets are not much worse than Kitano
  
• Networks built by the Nolfi method are noticeably worse than Kitano and Miller
  
• Networks built by the Kangelossi method are even worse than Nolfe.
  

However, it is noted that the best networks built using two “bad” methods (Nolfi and Kangelossi) demonstrate a significantly greater potential for learning when they are trained several times with different random weights.

In [6], NEAT is compared with some other techniques (evolutionary programming [7], conventional neuroevolution [8], Sane [9], and ESP [10]). The results of the comparison on one of the tasks (balancing with two poles — see details in [11]) are listed in the table.

Method	Evaluations	Generations	No. Nets
Ev. Programming 307,200 150 2048	307,200	150	2048
Conventional NE	80,000	800	100
SANE	12,600	63	200
Esp	3,800	nineteen	200
NEAT	3,600	24	150

As you can see, NEAT behaves much better than most of the compared methods (not surprising, given that the data were published by the authors of the methodology), however, again, these data need to be checked in other problem areas.

Instead of conclusion [3]

The combined use of evolutionary algorithms and ANNs allows solving the tasks of tuning and learning of the ANN both individually and simultaneously. One of the advantages of such a synthesized approach is in many respects a unified approach to solving various problems of classification, approximation, control, and modeling.Using a qualitative assessment of the functioning of the ANN allows you to apply neuroevolutionary algorithms to solve the problems of studying the adaptive behavior of intelligent agents, searching for game strategies, and signal processing. Despite the fact that the number of problems and open questions concerning the development and application of NE algorithms (coding methods, genetic operators, analysis methods, etc.) is large, it is often enough to successfully solve a problem using the NE algorithm to adequately understand the problem and the NE approach, evidence What is a large number of interesting and successful work in this direction.

[1] - Evolutionary neural network models with an unspecified number of connections
[2] - Properties of genetic representations of neural architectures (1995, Karthik Balakrishnan, Vasant Honavar)
[3] - An evolutionary approach to setting up and training artificial neural networks (2006, Tsoi Yu.R., Spitsyn VG)
[4 ] - Evolving Neural Networks (2009, Risto Miikkulainen and Kenneth O. Stanley)
[5] - Evolutionary Design of Neural Networks (1998, Marko A. Gronroos)
[6] - Evolving Neural Networks through Augmenting Topologies (2002, KO Stanley and R Miikkulainen)
[7] - Evolving neural control systems (1995, Saravanan, N. and Fogel, DB)
[8] - Evolving neural network control systems for unstable systems (1991, Wieland, A.)
[9] - SANE
[10] — Learning robust nonlinear control with neuroevolution (2002, Gomez, F. and Miikkulainen, R.)
[11] — Pole Balance Tutorial