Fibonacci numbers (etude on C #)
Probably many students had to study recursion using the example of calculating Fibonacci numbers. The problem is unconditionally academic, and it illustrates the recursion is clearly worse than the calculation of, say, factorials, but it is interesting because it has many solutions of different degrees of perversion. In this post - a small sketch on this topic.
I think that the default solution for calculating the N-th Fibonacci number will not surprise anyone:
Also, there is a rather “fashionable” form of the record of this solution which uses the Y-combinator:
')
Where
For large N, this approach is unproductive. How to calculate the number N faster? First, let's remember why, for example,
Why am I doing this? To the fact that the Fibonacci number can be calculated using the following formula:
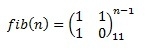
Now I understand why we integer exponentiation? For matrices, you can do the same, but first you need to understand how this is generally done. On the Internet, I found a possibly perfect algorithm that optimizes integer exponentiation. Please note that in the example below, the degree is of type
Now it remains to determine the 2 × 2 matrix. Here one could use some kind of library, but I decided to write the simplest possible structure:
After that, it was necessary to determine two constants that will be useful to us - the matrix that we will raise to the power and the identity matrix:
Now we can rewrite the
And define a new method to calculate the Fibonacci number:
That's all. I think that comparing the performance is meaningless - I have
I think that the default solution for calculating the N-th Fibonacci number will not surprise anyone:
static int fib(int n) { return n > 1 ? fib(n - 1) + fib(n - 2) : n; } Also, there is a rather “fashionable” form of the record of this solution which uses the Y-combinator:
')
Func<int, int> fib = Y<int,int>(f => n => n > 1 ? f(n - 1) + f(n - 2) : n); Where
Y defined, for example, like this: static Func<A, R> Y<A, R>(Func<Func<A, R>, Func<A, R>> f) { Func<A, R> g = null; g = f(a=>g(a)); return g; } For large N, this approach is unproductive. How to calculate the number N faster? First, let's remember why, for example,
x*x is considered faster than Math.Pow(x,2) ? Because for the integer degree, you can not only do without the Taylor series, but also optimize the calculation for large degrees by creating temporary variables. For example, x 4 can be considered as int y = x * x; return y * y; int y = x * x; return y * y; - and the greater the degree, the greater the savings.Why am I doing this? To the fact that the Fibonacci number can be calculated using the following formula:
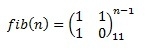
Now I understand why we integer exponentiation? For matrices, you can do the same, but first you need to understand how this is generally done. On the Internet, I found a possibly perfect algorithm that optimizes integer exponentiation. Please note that in the example below, the degree is of type
short . public static long IntPower(int x, short power) { if (power == 0) return 1; if (power == 1) return x; int n = 15; while ((power <<= 1) >= 0) n--; long tmp = x; while (--n > 0) tmp = tmp * tmp * (((power <<= 1) < 0) ? x : 1); return tmp; } Now it remains to determine the 2 × 2 matrix. Here one could use some kind of library, but I decided to write the simplest possible structure:
struct mtx2x2 { public int _11, _12, _21, _22; public static mtx2x2 operator*(mtx2x2 lhs, mtx2x2 rhs) { return new mtx2x2 { _11 = lhs._11*rhs._11 + lhs._12*rhs._21, _12 = lhs._11*rhs._12 + lhs._12*rhs._22, _21 = lhs._21*rhs._11 + lhs._22*rhs._21, _22 = lhs._21*rhs._12 + lhs._22*rhs._22 }; } } After that, it was necessary to determine two constants that will be useful to us - the matrix that we will raise to the power and the identity matrix:
private static readonly mtx2x2 fibMtx = new mtx2x2 {_11 = 1, _12 = 1, _21 = 1}; private static readonly mtx2x2 identity = new mtx2x2 {_11 = 1, _22 = 1}; Now we can rewrite the
IntPower() method for 2 × 2 matrices: public static mtx2x2 IntPower(mtx2x2 x, short power) { if (power == 0) return identity; if (power == 1) return x; int n = 15; while ((power <<= 1) >= 0) n--; mtx2x2 tmp = x; while (--n > 0) tmp = (tmp * tmp) * (((power <<= 1) < 0) ? x : identity); return tmp; } And define a new method to calculate the Fibonacci number:
static int fibm(short n) { return IntPower(fibMtx, (short)(n-1))._11; } That's all. I think that comparing the performance is meaningless - I have
fib(40) considered 4 seconds, and fibm(40) is displayed immediately. ■Source: https://habr.com/ru/post/83303/
All Articles