The theory and practice of the game "Battleship" - to be honest
Reading Habr once again, I became interested in the article “Sea battle with artificial intelligence - to be honest” and the program “Intellectual sea battle”.
Having tried to play with it, I found that the program’s strategy leaves much to be desired, because the score was 9: 1 in my favor.
I decided to share my thoughts with everyone, and in particular with the author ( michurin ) of the program, since the project is very interesting.
Attention!
After reading this article, the outcome of the game “Sea Battle” will cease to be an accident for you.
The article was written in simple language without the use of formulas.
"Any formula included in the book reduces the number of its customers by half" Stephen Hawking.
')
I would like to state in an easy and accessible manner an algorithm that I read a long time ago in the book by E.Ya. Geek " Entertaining math games ."
(When writing the article, the algorithm was supplemented)
The whole strategy will be described for the "Classic" sea battle
(a field of 10x10 each player has one chetyrehtrubnik, two trekhbrubnika, three dvuhtrubnika and four one-pipers).
Ships cannot bend.
Ships cannot touch.
The player makes 1 shot, if he misses, then the move goes to the opponent,
if it hits, it still shoots before the first slip).
Of course the success of the game, to some extent depends on luck. You can randomly strike at enemy territory and destroy all of its ships without a miss.
This strategy will not give you 100% victory, but will increase the probability of your victory to the maximum.
We had a girl in the class, so she didn’t expose a single-tube ship to the last, but an honest strategy will be described here.
The strategy consists of 2 parts.
1) Proper placement of ships.
2) Correct shooting at the enemy.
The correct placement of the ships.
This idea has already been mentioned in the above article , I will repeat it and sign it in detail for those who do not know.
The essence of the idea to arrange the ships so as to reduce the likelihood of hitting them.
The hardest thing is to get into the one-pipe; our task is to arrange the rest of the ships on the minimum area, in order to leave as much space as possible for one-pipe.
This arrangement is the arrangement "at the edges" or "around the perimeter."
Thus, when all the “big” ships are sunk, it will be very difficult to search for single-pipe ones.
I will show by example:
I tried to keep the color scheme, as in the above game.
Yellow = ships
Blue = Superstructure (a place around the ship where the adjacent ship cannot be located)
Sea wave (cyan) = the remaining area for the arrangement of monotrans.

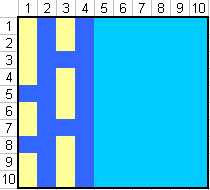
When writing an article, an arrangement was accidentally found, which was not in the considered in the book.
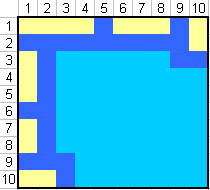
Layouts can also turn out to be mirror reflections both vertically and horizontally, as well as turning the field 90, 180, 270 degrees.
The area remaining for the placement of 4 single-tube ships, it turns out 60 cells. Consequently, the probability of hitting a one-pipe ship is 4 out of 60 or 6.67%. With other arrangements, the probability of hitting is higher.
Consider an arbitrary arrangement that was proposed by the program.
(I removed the monotubes for the purity of the experiment).

33 cells for placement of 4 single-tube ships, it is almost 2 times smaller
those. my probability of winning was almost 2! times higher (not taking into account the optimal shooting).
Correct shooting at the enemy
The idea of correct shooting is as follows.
First you need to try to get into the largest ship (for the classics it’s 4 pipe), since it is probabilistically easier to get into it than in a monotube.
We divide the field into 4x4 areas (arbitrarily). It should turn out 4 full squares and all that remains.

To do this, there are 7 combinations that can also be expanded by means of mirror reflections and turns. With such a space, it is impossible to inscribe a four-pipe in a 4x4 square.

The whole field is shot through in any sequence, observing the combination.

If we get into a ship, then we must finish it to the end.
After the ship has been hit, a superstructure is drawn around it in a single cell,
so there is no reason to not shoot.
Further, when the 4th pipe has been sunk, we are looking for 3 pipe manufacturers, we are clearing sparingly fields so that it will not be possible to install the 3 pipe manufacturers.
We divide the field into 3x3 squares. We shoot so that it was impossible to put 3 pipe.

And so on. We reach the monotonous, then how lucky.
Well, in principle, that's all.
After everyone in the class knew this strategy, we moved on to the game “Sea Battle” (4 single-columnists are on the 5x5 field).
After that, the game began to be more psychological in nature (who repeats or does not repeat when placing) than the mathematical one.
Conclusion:
I propose to the author ( michurin ) of the “Sea battle with intellect” to adopt this strategy and use it in parts, depending on the set intellect level of the program.
PS When writing this article, no ship of the Navy was hurt =).
PS2 My games with the program:



UPD Fixed pictures (transferred from pict.com to imagehack), but they are still not visible.
UPD2 I put everything on habrastorage.org like everything is visible.
Having tried to play with it, I found that the program’s strategy leaves much to be desired, because the score was 9: 1 in my favor.
I decided to share my thoughts with everyone, and in particular with the author ( michurin ) of the program, since the project is very interesting.
Attention!
After reading this article, the outcome of the game “Sea Battle” will cease to be an accident for you.
The article was written in simple language without the use of formulas.
"Any formula included in the book reduces the number of its customers by half" Stephen Hawking.
')
I would like to state in an easy and accessible manner an algorithm that I read a long time ago in the book by E.Ya. Geek " Entertaining math games ."
(When writing the article, the algorithm was supplemented)
The whole strategy will be described for the "Classic" sea battle
(a field of 10x10 each player has one chetyrehtrubnik, two trekhbrubnika, three dvuhtrubnika and four one-pipers).
Ships cannot bend.
Ships cannot touch.
The player makes 1 shot, if he misses, then the move goes to the opponent,
if it hits, it still shoots before the first slip).
Of course the success of the game, to some extent depends on luck. You can randomly strike at enemy territory and destroy all of its ships without a miss.
This strategy will not give you 100% victory, but will increase the probability of your victory to the maximum.
We had a girl in the class, so she didn’t expose a single-tube ship to the last, but an honest strategy will be described here.
The strategy consists of 2 parts.
1) Proper placement of ships.
2) Correct shooting at the enemy.
The correct placement of the ships.
This idea has already been mentioned in the above article , I will repeat it and sign it in detail for those who do not know.
The essence of the idea to arrange the ships so as to reduce the likelihood of hitting them.
The hardest thing is to get into the one-pipe; our task is to arrange the rest of the ships on the minimum area, in order to leave as much space as possible for one-pipe.
This arrangement is the arrangement "at the edges" or "around the perimeter."
Thus, when all the “big” ships are sunk, it will be very difficult to search for single-pipe ones.
I will show by example:
I tried to keep the color scheme, as in the above game.
Yellow = ships
Blue = Superstructure (a place around the ship where the adjacent ship cannot be located)
Sea wave (cyan) = the remaining area for the arrangement of monotrans.


When writing an article, an arrangement was accidentally found, which was not in the considered in the book.

Layouts can also turn out to be mirror reflections both vertically and horizontally, as well as turning the field 90, 180, 270 degrees.
The area remaining for the placement of 4 single-tube ships, it turns out 60 cells. Consequently, the probability of hitting a one-pipe ship is 4 out of 60 or 6.67%. With other arrangements, the probability of hitting is higher.
Consider an arbitrary arrangement that was proposed by the program.
(I removed the monotubes for the purity of the experiment).

33 cells for placement of 4 single-tube ships, it is almost 2 times smaller
those. my probability of winning was almost 2! times higher (not taking into account the optimal shooting).
Correct shooting at the enemy
The idea of correct shooting is as follows.
First you need to try to get into the largest ship (for the classics it’s 4 pipe), since it is probabilistically easier to get into it than in a monotube.
We divide the field into 4x4 areas (arbitrarily). It should turn out 4 full squares and all that remains.

To do this, there are 7 combinations that can also be expanded by means of mirror reflections and turns. With such a space, it is impossible to inscribe a four-pipe in a 4x4 square.

The whole field is shot through in any sequence, observing the combination.

If we get into a ship, then we must finish it to the end.
After the ship has been hit, a superstructure is drawn around it in a single cell,
so there is no reason to not shoot.
Further, when the 4th pipe has been sunk, we are looking for 3 pipe manufacturers, we are clearing sparingly fields so that it will not be possible to install the 3 pipe manufacturers.
We divide the field into 3x3 squares. We shoot so that it was impossible to put 3 pipe.

And so on. We reach the monotonous, then how lucky.
Well, in principle, that's all.
After everyone in the class knew this strategy, we moved on to the game “Sea Battle” (4 single-columnists are on the 5x5 field).
After that, the game began to be more psychological in nature (who repeats or does not repeat when placing) than the mathematical one.
Conclusion:
I propose to the author ( michurin ) of the “Sea battle with intellect” to adopt this strategy and use it in parts, depending on the set intellect level of the program.
PS When writing this article, no ship of the Navy was hurt =).
PS2 My games with the program:







UPD Fixed pictures (transferred from pict.com to imagehack), but they are still not visible.
UPD2 I put everything on habrastorage.org like everything is visible.
Source: https://habr.com/ru/post/82221/
All Articles