Adaptive boosting
Hello, on Habré was already an article Indalo , dedicated to AdaBoost, more precisely, some of its application. I want to dwell in more detail on the algorithm itself, to look into its implementation and demonstrate its work using the example of my program.
So what is the essence of the Adaboost methodology?
The bottom line is that if we have a set of reference objects (points on a plane), i.e. there are values and a class to which they belong (for example, -1 is a red dot, +1 is a blue dot), in addition there are a lot of simple classifiers (a set of vertical or horizontal lines that divide the plane into two parts with the smallest error), we can make one best classifier. At the same time, in the process of drawing up or training the final classifier, emphasis is placed on standards that are recognized “worse”, this is the adaptability of the algorithm, and in the process of training it adapts to the most “complex” objects.
The pseudocode of the algorithm is well described on the wiki . We give it here.
Given: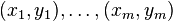 where
where 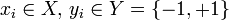 .
.
')
We initialize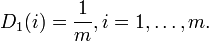
For each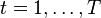 :
:
* Find a classifier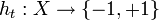 which minimizes the weighted classification error:
which minimizes the weighted classification error:
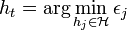 where
where 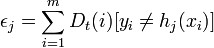
* If value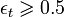 then stop.
then stop.
* Choose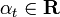 usually
usually 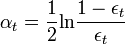 where? t is a weighted classifier error ht.
where? t is a weighted classifier error ht.
* Update:
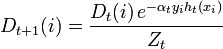 ,
,
where Zt is the normalizing parameter (selected so that Dt + 1 is the probability distribution, i.e.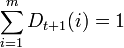 ).
).
Build the resulting classifier:
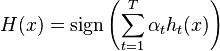 .
.
Further we will adhere to it in our explanations.
So, a simple classifier. As I said, this is a vertical or horizontal line that divides the plane into two parts, minimizing the classification error: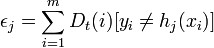 (brackets from a boolean expression are 1, ate true, and 0 if false). In C #, the procedure for such training can be written as follows:
(brackets from a boolean expression are 1, ate true, and 0 if false). In C #, the procedure for such training can be written as follows:
// Learning simple classifier
If you have noticed, the learning procedure of a simple classifier is written in such a way that if you transfer the weights that are obtained during the operation of the AdaBoost algorithm, then that classifier that minimizes the weighted classification error of claim 1 will be searched. Then the C # algorithm itself will look like this:
// Learning with AdaBoost
Thus, after choosing the optimal classifier h_ {t} \, for the distribution of D_i, the objects x_ {i} \ ,, which the classifier h_ {t} \ identifies correctly, have weights less than those that are identified incorrectly. Therefore, when an algorithm tests classifiers on the D_ {t + 1} distribution, it will select a classifier that better identifies objects that are incorrectly recognized by the previous classifier.
In the case of the classification of such data:

AdaBoost classified image will look like this:

For comparison, we can give a simple algorithm, which for each point determines its nearest neighbor, whose class is known. (It is clear that the cost of such an algorithm is very high.)

As you can see, an algorithm built using AdaBoost classifies much better than one classifier, but it also has errors. But the simplicity and elegance of the algorithm allowed him to enter the Top 10 algorithms in data mining . I hope the code in the article helped you to deal with this algorithm.
The full source code of the program and the program itself can be downloaded here .
PS As a continuation of the article, we can consider the case when the general classifier is not constructed as a linear function of weak classifiers, but, for example, a quadratic one. The authors of the article claim that they have found a way to effectively teach the quadratic function in this case. Or, in the continuation of the article, we can consider the case when there are more than two classes of objects.
So what is the essence of the Adaboost methodology?
The bottom line is that if we have a set of reference objects (points on a plane), i.e. there are values and a class to which they belong (for example, -1 is a red dot, +1 is a blue dot), in addition there are a lot of simple classifiers (a set of vertical or horizontal lines that divide the plane into two parts with the smallest error), we can make one best classifier. At the same time, in the process of drawing up or training the final classifier, emphasis is placed on standards that are recognized “worse”, this is the adaptability of the algorithm, and in the process of training it adapts to the most “complex” objects.
The pseudocode of the algorithm is well described on the wiki . We give it here.
Pseudocode
Given:
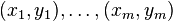 where
where 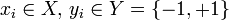 .
.')
We initialize
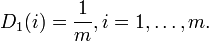
For each
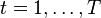 :
:* Find a classifier
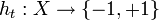 which minimizes the weighted classification error:
which minimizes the weighted classification error: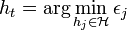 where
where 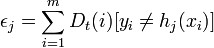
* If value
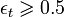 then stop.
then stop.* Choose
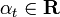 usually
usually 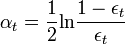 where? t is a weighted classifier error ht.
where? t is a weighted classifier error ht.* Update:
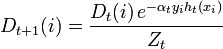 ,
,where Zt is the normalizing parameter (selected so that Dt + 1 is the probability distribution, i.e.
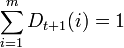 ).
).Build the resulting classifier:
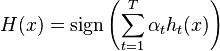 .
.Further we will adhere to it in our explanations.
Simple classifier
So, a simple classifier. As I said, this is a vertical or horizontal line that divides the plane into two parts, minimizing the classification error:
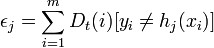 (brackets from a boolean expression are 1, ate true, and 0 if false). In C #, the procedure for such training can be written as follows:
(brackets from a boolean expression are 1, ate true, and 0 if false). In C #, the procedure for such training can be written as follows:// Learning simple classifier
public override void Train(LabeledDataSet< double > trainingSet)
{
// D_i
if (_weights == null )
{
_weights = new double [trainingSet.Count];
for ( int i = 0; i < trainingSet.Count; i++)
_weights[i] = 1.0 / trainingSet.Count;
}
Random rnd = new Random();
double minimumError = double .PositiveInfinity;
_d = -1;
_threshold = double .NaN;
_sign = 0;
//
for ( int d = 0; d < trainingSet.Dimensionality; d++)
{
// ,
if (rnd.NextDouble() < _randomize)
continue ;
// x_d = threshold
double [] data = new double [trainingSet.Count];
int [] indices = new int [trainingSet.Count];
for ( int i = 0; i < trainingSet.Count; i++)
{
data[i] = trainingSet.Data[i][d];
indices[i] = i;
}
Array.Sort(data, indices);
//
double totalError = 0.0;
for ( int i = 0; i < trainingSet.Count; i++)
totalError += _weights[i];
//
double currentError = 0.0;
for ( int i = 0; i < trainingSet.Count; i++)
currentError += trainingSet.Labels[i] == -1 ? _weights[i] : 0.0;
// threshold,
//,
for ( int i = 0; i < trainingSet.Count - 1; i++)
{
//
int index = indices[i];
if (trainingSet.Labels[index] == +1)
currentError += _weights[index];
else
currentError -= _weights[index];
// ,
if (data[i] == data[i + 1])
continue ;
// threshold
double testThreshold = (data[i] + data[i + 1]) / 2.0;
// threshold, ,
if (currentError < minimumError) // _sign = +1
{
minimumError = currentError;
_d = d;
_threshold = testThreshold;
_sign = +1;
}
if ((totalError - currentError) < minimumError) // _sign = -1
{
minimumError = (totalError - currentError);
_d = d;
_threshold = testThreshold;
_sign = -1;
}
}
}
}If you have noticed, the learning procedure of a simple classifier is written in such a way that if you transfer the weights that are obtained during the operation of the AdaBoost algorithm, then that classifier that minimizes the weighted classification error of claim 1 will be searched. Then the C # algorithm itself will look like this:
"Difficult" classifier
// Learning with AdaBoost
public override void Train(LabeledDataSet< double > trainingSet)
{
// D_i
if (_weights == null )
{
_weights = new double [trainingSet.Count];
for ( int i = 0; i < trainingSet.Count; i++)
_weights[i] = 1.0 / trainingSet.Count;
}
//
for ( int t = _h.Count; t < _numberOfRounds; t++)
{
//
WeakLearner h = _factory();
h.Weights = _weights;
h.Train(trainingSet);
//
int [] hClassification = new int [trainingSet.Count];
double epsilon = 0.0;
for ( int i = 0; i < trainingSet.Count; i++)
{
hClassification[i] = h.Classify(trainingSet.Data[i]);
epsilon += hClassification[i] != trainingSet.Labels[i] ? _weights[i] : 0.0;
}
// epsilon >= 0.5,
if (epsilon >= 0.5)
break ;
// \alpha_{t}
double alpha = 0.5 * Math.Log((1 - epsilon) / epsilon);
// D_i
double weightsSum = 0.0;
for ( int i = 0; i < trainingSet.Count; i++)
{
_weights[i] *= Math.Exp(-alpha * trainingSet.Labels[i] * hClassification[i]);
weightsSum += _weights[i];
}
//
for ( int i = 0; i < trainingSet.Count; i++)
_weights[i] /= weightsSum;
//
_h.Add(h);
_alpha.Add(alpha);
// ,
if (epsilon == 0.0)
break ;
}
}Thus, after choosing the optimal classifier h_ {t} \, for the distribution of D_i, the objects x_ {i} \ ,, which the classifier h_ {t} \ identifies correctly, have weights less than those that are identified incorrectly. Therefore, when an algorithm tests classifiers on the D_ {t + 1} distribution, it will select a classifier that better identifies objects that are incorrectly recognized by the previous classifier.
Example
In the case of the classification of such data:

AdaBoost classified image will look like this:

For comparison, we can give a simple algorithm, which for each point determines its nearest neighbor, whose class is known. (It is clear that the cost of such an algorithm is very high.)

Conclusion
As you can see, an algorithm built using AdaBoost classifies much better than one classifier, but it also has errors. But the simplicity and elegance of the algorithm allowed him to enter the Top 10 algorithms in data mining . I hope the code in the article helped you to deal with this algorithm.
The full source code of the program and the program itself can be downloaded here .
PS As a continuation of the article, we can consider the case when the general classifier is not constructed as a linear function of weak classifiers, but, for example, a quadratic one. The authors of the article claim that they have found a way to effectively teach the quadratic function in this case. Or, in the continuation of the article, we can consider the case when there are more than two classes of objects.
Source: https://habr.com/ru/post/80323/
All Articles