Map / Reduce: solving real problems - TF-IDF - 2
Continuing the article “ Using Hadoop to solve real problems ”, I want to remind you that in the last article we stopped at what we considered such a characteristic as tf (t, d) , and said that in the next post we will consider idf (t) and complete the process of calculating the TF-IDF value for this document and term. Therefore, I suggest not to postpone for a long time and move on to this task.
It is important to note that idf (t) does not depend on the document, because it is considered on the whole body. It is easy to see, looking at the formula:
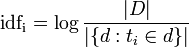
')
She probably needs some explanation. So, | D | This is the power of the body of documents - in other words, just the number of documents. We know him, so nothing should be considered. The denominator of the logarithm is the number of such documents d that contain the token of interest to us t_i .
How can this be calculated? There are many ways, but I suggest the following. As input, we will use the result of the task, which calculated unnormalized tf (t, d) values for us, reminding you that they looked like this:
What will be our task? We want to understand: how many, for example, documents contain the word
By doing this for all documents, we get the data in the following format:
Then everything is more or less obvious: reduce-task receives this data (it receives the term and the list of units), counts the number of these very units and gives us:
Q.E.D. Now the task to calculate directly idf (t) becomes trivial (however, it can also be done on the grid, simply because the list of words can be very large).
In the last step, we consider directly TF-IDF. This is where the trouble begins! The thing is that we have two files - one with TF values, the other with IDF values. In general, neither one nor the other will get into the memory. What to do? Dead end!
Dead end, but not quite. Here helps such a strange, but very popular in Map / Reduce solution as data pass- through (passthrough). I will explain my idea with an example. If processing our file with TF values (see above), instead of one in the output of the map task we will write the combination
We can still count the number of documents that includes one or another word - and indeed, we did not summarize the units but simply counted their number! At the same time, we have some additional data, which means we can modify the output of the reduce task as follows:
We have the following funny situation - the reducer didn’t actually reduce the amount of data, but added some new characteristics to them! What can we do now? Yes, almost anything! Assuming that we know the values of N and | D | (that is, the number of tokens and the number of documents in the package), we can implement the simplest Map / Reduce program (which Reduce will not be needed). For each incoming line, it will represent the data as follows
I hope you understand that pseudocode is very, very conditional (as well as conditional use of the underscore character to separate values) - but the essence, it seems to me, is clear. Now we can do the following:
What have we got? We got the value of TF-IDF.
In this article, we have completed an example of calculating the TF-IDF value for text boxes. It is important to note that increasing the capacity of the case will not lead to possible problems with a lack of memory, but will only increase the computation time (which can be solved by adding new nodes to the cluster). We looked at one of the popular data passthrough techniques, often used to solve complex problems in Map / Reduce. We have learned some of the design principles for Map / Reduce applications in general. In future articles we will look at solving this and other problems for real data, with examples of working code.
PS as always, questions, comments, clarifications and feedback are welcome! I tried to make it all as clear as possible, but maybe not quite succeeded - write me about it!
For home reading, I recommend viewing the slides posted by comrades from Cloudera on Scribd:
For those interested, I also remind you that the English version of the article (in its entirety) is available here: romankirillov.info/hadoop.html - you can also download a PDF version there.
It is important to note that idf (t) does not depend on the document, because it is considered on the whole body. It is easy to see, looking at the formula:
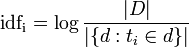
')
She probably needs some explanation. So, | D | This is the power of the body of documents - in other words, just the number of documents. We know him, so nothing should be considered. The denominator of the logarithm is the number of such documents d that contain the token of interest to us t_i .
How can this be calculated? There are many ways, but I suggest the following. As input, we will use the result of the task, which calculated unnormalized tf (t, d) values for us, reminding you that they looked like this:
1_the 3 1_to 1 ... 2_the 2 2_from 1 ... 37_london 1
What will be our task? We want to understand: how many, for example, documents contain the word
the ? The solution, in general, is intuitive: we take each value, such as 2_the , divide it by a pair ( 2 , the ) and write to the output of the map-task that we have at least one document that contains the word the :the 1
By doing this for all documents, we get the data in the following format:
the 1 to 1 the 1 from 1 london 1
Then everything is more or less obvious: reduce-task receives this data (it receives the term and the list of units), counts the number of these very units and gives us:
the 2 to 1 from 1 london 1
Q.E.D. Now the task to calculate directly idf (t) becomes trivial (however, it can also be done on the grid, simply because the list of words can be very large).
In the last step, we consider directly TF-IDF. This is where the trouble begins! The thing is that we have two files - one with TF values, the other with IDF values. In general, neither one nor the other will get into the memory. What to do? Dead end!
Dead end, but not quite. Here helps such a strange, but very popular in Map / Reduce solution as data pass- through (passthrough). I will explain my idea with an example. If processing our file with TF values (see above), instead of one in the output of the map task we will write the combination
docID_tfValue ? Something will turn out like:the 1_3 to 1_3 the 2_2 from 2_1 ... london 37_1
We can still count the number of documents that includes one or another word - and indeed, we did not summarize the units but simply counted their number! At the same time, we have some additional data, which means we can modify the output of the reduce task as follows:
the 2_1_3 # number of documents with the - document identifier - the number in this doc the 2_2_2 to 1_1_3 from 1_2_1 ... london 1_37_1
We have the following funny situation - the reducer didn’t actually reduce the amount of data, but added some new characteristics to them! What can we do now? Yes, almost anything! Assuming that we know the values of N and | D | (that is, the number of tokens and the number of documents in the package), we can implement the simplest Map / Reduce program (which Reduce will not be needed). For each incoming line, it will represent the data as follows
term = key
(docCount, docId, countInDoc) = value.split ("_") I hope you understand that pseudocode is very, very conditional (as well as conditional use of the underscore character to separate values) - but the essence, it seems to me, is clear. Now we can do the following:
tf = countInDoc / TOTAL_TOKEN_COUNT idf = log (TOTAL_DOC_COUNT / docCount) result = tf * idf output (key = docId + "_" + term, value = result)
What have we got? We got the value of TF-IDF.
In this article, we have completed an example of calculating the TF-IDF value for text boxes. It is important to note that increasing the capacity of the case will not lead to possible problems with a lack of memory, but will only increase the computation time (which can be solved by adding new nodes to the cluster). We looked at one of the popular data passthrough techniques, often used to solve complex problems in Map / Reduce. We have learned some of the design principles for Map / Reduce applications in general. In future articles we will look at solving this and other problems for real data, with examples of working code.
PS as always, questions, comments, clarifications and feedback are welcome! I tried to make it all as clear as possible, but maybe not quite succeeded - write me about it!
For home reading, I recommend viewing the slides posted by comrades from Cloudera on Scribd:
- Hadoop Training # 1: Thinking at Scale
- Hadoop Training # 2: MapReduce & HDFS
- ... and the rest of the presentations from this series.
For those interested, I also remind you that the English version of the article (in its entirety) is available here: romankirillov.info/hadoop.html - you can also download a PDF version there.
Source: https://habr.com/ru/post/74934/
All Articles