The use of neural networks in image recognition
Quite a lot has already been said about neural networks as one of the tools for solving difficult-to-formalize tasks. And here, in Habré, it was shown how to use these networks for image recognition as applied to the captcha hacking task. However, there are quite a few types of neural networks. And is the classical fully connected neural network (PNS) good for image recognition (classification) problems?
So, we are going to solve the problem of image recognition. This may be face recognition, objects, symbols, etc. I propose to begin to consider the problem of recognizing handwritten numbers. This task is good for several reasons:
It is proposed to use the MNIST database as input data. This database contains 60,000 training pairs (image - label) and 10,000 test pairs (images without labels). Images are normalized in size and centered. The size of each digit is no more than 20x20, but they are inscribed in a square measuring 28x28. An example of the first 12 digits from the MNIST training set is shown in the figure:

Thus, the task is formulated as follows: create and train a neural network to recognize handwritten characters, taking their images at the input and activating one of the 10 outputs . By activation we mean the value 1 at the output. The values of the remaining outputs in this case should (ideally) be equal to -1. Why it does not use the scale [0,1] I will explain later.
Most people by “normal” or “classical” neural networks understand fully connected neural networks of direct propagation with back propagation of an error:

As the name implies, in such a network, each neuron is connected to each, the signal goes only in the direction from the input layer to the output, there are no recursions. We will call such a network abbreviated PNS.
First you need to decide how to input data. The simplest and almost no alternative solution for PNS is to express a two-dimensional image matrix in the form of a one-dimensional vector. Those. for the image of a handwritten digit of 28x28, we will have 784 entries, which is no small. What happens next is what many conservative scientists don’t like for neural networkers and their methods - the choice of architecture. They do not like it, since the choice of architecture is pure shamanism. So far, there are no methods to unambiguously determine the structure and composition of a neural network based on the task description. In defense, I will say that for hardly-formalized tasks such a method will hardly ever be created. In addition, there are many different methods of network reduction (for example, OBD [1]), as well as various heuristics and rules of thumb. One of these rules says that the number of neurons in the hidden layer must be at least an order of magnitude greater than the number of inputs. If we take into account that the transformation from the image to the class indicator itself is quite complex and essentially nonlinear, you cannot do with a single layer. Based on the foregoing, we roughly estimate that the number of neurons in the hidden layers will be about 15,000 (10,000 in the 2nd layer and 5,000 in the third). At the same time, for a configuration with two hidden layers, the number of configured and trained links will be 10 million between the inputs and the first hidden layer + 50 million between the first and second + 50 thousand between the second and the output, if we assume that we have 10 outputs, each of which denotes a number from 0 to 9. Total roughly 60 million links . I knowingly mentioned that they are customizable - this means that when training for each of them it will be necessary to calculate the error gradient.
Well, it's okay, what can you do here, thebeauty of artificial intelligence requires sacrifice. But if you think about it, it comes to mind that when we convert an image into a linear chain of bytes, we are irretrievably losing something. Moreover, with each layer, this loss is only aggravated. So it is - we lose the image topology, i.e. the relationship between its individual parts. In addition, the task of mapping implies the ability of a neural network to be resistant to small shifts, rotations and zooming, i.e. it must extract from the data some invariants that do not depend on the handwriting of this or that person. So what should a neural network be to be not very computationally complex and, at the same time, more invariant to various image distortions?
')
A solution to this problem was found by American scientist of French origin, Jan LeCoun , inspired by the works of Nobel laureates in the field of medicine Torsten Nils Wiesel and David H. Hubel . These scientists investigated the cat's visual cortex and found that there are so-called simple cells that are particularly responsive to straight lines from different angles and complex cells that react to the movement of lines in one direction. Jan LeKun proposed the use of so-called convolutional neural networks [2].
The idea of convolutional neural networks is the alternation of convolutional layers (C-layers), subsampling layers (S-layers) and the presence of fully connected (F-layers) layers at the output.
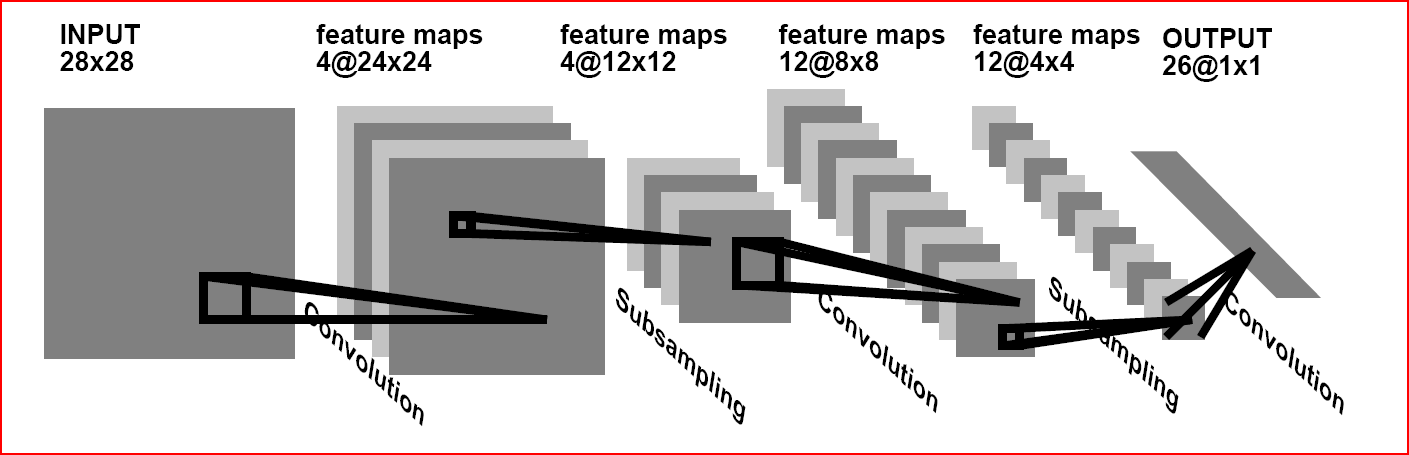
This architecture has 3 main paradigms:
Local perception implies that not all of the image (or outputs of the previous layer) is fed to the input of one neuron, but only some of its area. This approach allowed us to maintain the topology of the image from layer to layer.
The concept of shared weights suggests that for a large number of links a very small set of weights is used. Those. if we have an image with the size of 32x32 pixels at the input, then each of the neurons of the next layer will receive only a small section of this image, for example, 5x5, and each of the fragments will be processed with the same set. It is important to understand that the sets of scales themselves can be many, but each of them will be applied to the entire image. Such kits are often called kernels. It is easy to calculate that even for 10 cores 5x5 in size for an input image 32x32 in size, the number of links will be approximately 256,000 (compare with 10 million), and the number of adjustable parameters is only 250!
And what, you ask, will this affect the quality of recognition? Oddly, for the better. The fact is that such an artificially imposed weight limit improves the generalizing properties of the network (generalization), which ultimately has a positive effect on the network's ability to find invariants in the image and react mainly to them, without paying attention to other noise. You can look at this approach a bit from the other side. Those who are engaged in image recognition classics and know how it works in practice (for example, in military technology) know that most of such systems are built on the basis of two-dimensional filters. The filter is a matrix of coefficients, usually manually defined. This matrix is applied to the image using a mathematical operation called convolution . The essence of this operation is that each image fragment is multiplied by the convolution matrix (core) element by element and the result is summed up and written to the similar position of the output image. The main property of such filters is that the value of their output is the greater, the more a fragment of the image is similar to the filter itself. Thus, the image is minimized with a certain core and it will give us a different image, each pixel of which will mean the degree of similarity of a fragment of the image to the filter. In other words, it will be a feature map.
The process of propagation of the signal in the C-layer, I tried to depict in the figure:
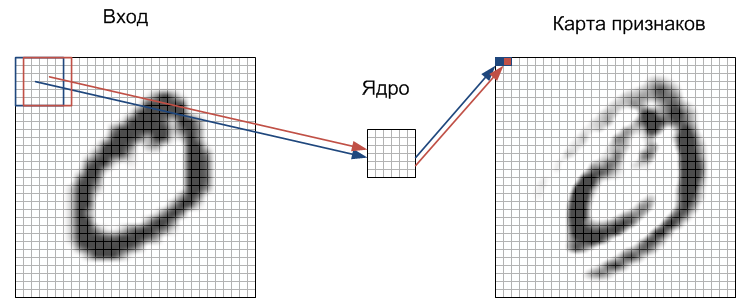
Each fragment of the image is multiplied element by element by a small matrix of weights (the core), the result is summed up. This sum is the pixel of the output image, which is called the attribute map. Here I omitted the fact that the weighted sum of inputs is still passed through the activation function (as in any other neural network). In fact, this can happen in the S-layer, there is no fundamental difference. It should be said that, ideally, not different fragments pass sequentially through the core, and in parallel the entire image passes through identical nuclei. In addition, the number of cores (sets of weights) is determined by the developer and depends on how many signs you need to select. Another feature of the convolutional layer is that it slightly reduces the image due to edge effects.
The essence of subsampling and S-layers is to reduce the spatial dimension of the image. Those. the input image is roughly (averaged) reduced by a specified number of times. Most often, 2 times, although there may be a non-uniform change, for example, 2 vertically and 3 horizontally. Subsampling is necessary to ensure scale invariance.
The alternation of layers allows mapping of features from feature maps, which in practice means the ability to recognize complex feature hierarchies.
Usually, after passing through several layers, the feature map degenerates into a vector or even a scalar, but there are hundreds of such feature maps. In this form, they are fed to one or two layers of a fully connected network. The output layer of such a network can have various activation functions. In the simplest case, this may be a tangential function, and radial basis functions are also successfully used.
In order to start learning our network, you need to decide how to measure the quality of recognition. In our case, for this we will use the most common in the theory of neural networks the function of mean square error (MSE) [3]:
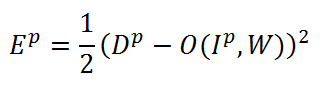
In this formula, Ep is a recognition error for the p-th training pair, Dp is the desired network output, O (Ip, W) is the network output, depending on the p-th input and weighting factors W, which include convolution kernels, displacements, weighting coefficients of S- and F-layers. The task of training is to adjust the weights W so that they give the minimal error Ep for any training pair (Ip, Dp). To calculate the error for the entire training sample, simply take the arithmetic average for errors for all training pairs. This average error is denoted by E.
To minimize the error function Ep, gradient methods are most effective. Consider the essence of gradient methods on the example of the simplest one-dimensional case (that is, when we have only one weight). If we decompose the error function Ep into the Taylor series, we get the following expression:
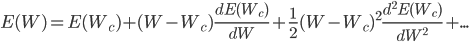
Here E is the same error function, Wc is some initial value of the weight. From school mathematics we remember that in order to find the extremum of a function, it is necessary to take its derivative and equate to zero. So let's do it, take the derivative of the error function with respect to weights, rejecting terms higher than 2nd order:
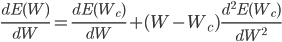
it follows from this expression that the weight at which the value of the error function will be minimal can be calculated from the following expression:
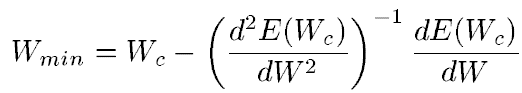
Those. the optimal weight is calculated as the current minus the derivative of the error function by weight divided by the second derivative of the error function. For the multidimensional case (i.e., for the weights matrix), everything is exactly the same, only the first derivative turns into a gradient (the vector of partial derivatives), and the second derivative turns into a Hessian (the matrix of the second partial derivatives). And here there are two options. If we omit the second derivative, we obtain an algorithm for the fastest gradient descent. If we still want to take into account the second derivative, we will be stunned by how many computing resources we need to calculate the full Hessian, and then also draw it. Therefore, usually the Hessian is replaced by something more simple. For example, one of the most well-known and successful methods, the Levenberg-Marquardt (LM) method, replaces the Hessian with its approximation using the Jacobian quadratic. Details here will not tell.
But what is important for us to know about these two methods is that the LM algorithm requires processing the entire training sample, whereas the gradient descent algorithm can work with each individual training sample. In the latter case, the algorithm is called a stochastic gradient. Given that our database contains 60,000 training samples, the stochastic gradient is more suitable for us. Another advantage of the stochastic gradient is that it is less susceptible to falling into a local minimum compared to LM.
There is also a stochastic modification of the LM algorithm, which I may mention later.
The presented formulas make it easy to calculate the error derivative with respect to weights located in the output layer. The error in hidden layers can be calculated using the widely known method of back propagation of errors in AI.
Personally, I use to implement various algorithms, from which Matlab does not require real-time operation. This is a very convenient package whose M-language allows you to focus on the algorithm itself without worrying about memory allocation, I / O operations, etc. In addition, many different toolboxes allow you to create truly interdisciplinary applications in the shortest possible time. For example, using the Image Acquisition Toolbox, you can connect a webcam, use the Image Processing Toolbox to process the image from it, use the Neural Network Toolbox to form the robot's trajectory, and use the Virtual Reality Toolbox and Control Systems Toolbox to simulate the robot's movement. Speaking of the Neural Network Toolbox, this is a fairly flexible set of tools that allows you to create many neural networks of various types and architectures, but, unfortunately, not convolutional NA. It's all about shared scales. In the NN toolbox, the ability to specify shared weights is missing.
To eliminate this drawback, I wrote a class that allows you to implement the SNA of an arbitrary architecture and apply them to various tasks. Download the class here . The class itself was written so that the one who uses it has the maximum visible network structure. Everything is very abundantly commented, did not save on the name of variables. Network simulation speed is not bad and is a fraction of a second. The learning rate is not yet high (> 10 hours), but stay tuned, in the near future we plan to accelerate by orders of magnitude.
Who is interested in the implementation of SNS in C ++, can find it here and here .
In the program on matlabcentral, a file of an already trained neural network is attached, as well as a GUI for demonstrating the results of work. The following are examples of recognition:

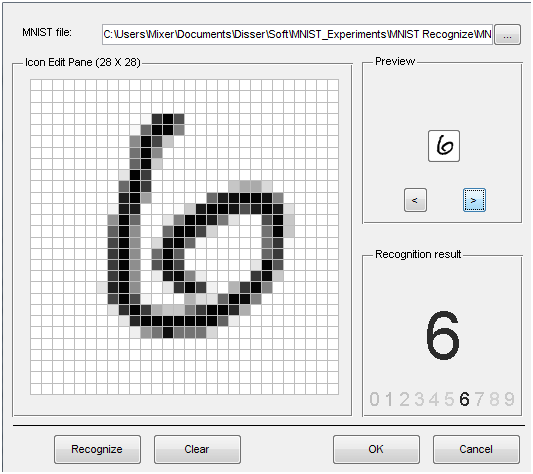
The link has a table of comparison of recognition methods based on MNIST. The first place is behind convolutional neural networks with the result of 0.39% recognition errors [4]. Most of these images are mistakenly recognized not every person correctly recognizes. In addition, elastic distortions of the input images were used in [4], as well as preliminary training without a teacher. But about these methods as in some other article.
PS Thank you all for the comments and feedback. This is my first article on Habré, so I will be happy to see suggestions, comments, additions.
1. Task
So, we are going to solve the problem of image recognition. This may be face recognition, objects, symbols, etc. I propose to begin to consider the problem of recognizing handwritten numbers. This task is good for several reasons:
- To recognize a handwritten symbol, it is rather difficult to compose a formalized (non-intelligent) algorithm, and this becomes clear, just look at the same number written by different people.
- The task is quite relevant and is related to OCR (optical character recognition)
- There is a freely distributable base of handwritten characters available for download and experimentation.
- There are quite a few articles on this topic and you can very easily compare the various approaches.
It is proposed to use the MNIST database as input data. This database contains 60,000 training pairs (image - label) and 10,000 test pairs (images without labels). Images are normalized in size and centered. The size of each digit is no more than 20x20, but they are inscribed in a square measuring 28x28. An example of the first 12 digits from the MNIST training set is shown in the figure:

Thus, the task is formulated as follows: create and train a neural network to recognize handwritten characters, taking their images at the input and activating one of the 10 outputs . By activation we mean the value 1 at the output. The values of the remaining outputs in this case should (ideally) be equal to -1. Why it does not use the scale [0,1] I will explain later.
2. “Normal” neural networks.
Most people by “normal” or “classical” neural networks understand fully connected neural networks of direct propagation with back propagation of an error:

As the name implies, in such a network, each neuron is connected to each, the signal goes only in the direction from the input layer to the output, there are no recursions. We will call such a network abbreviated PNS.
First you need to decide how to input data. The simplest and almost no alternative solution for PNS is to express a two-dimensional image matrix in the form of a one-dimensional vector. Those. for the image of a handwritten digit of 28x28, we will have 784 entries, which is no small. What happens next is what many conservative scientists don’t like for neural networkers and their methods - the choice of architecture. They do not like it, since the choice of architecture is pure shamanism. So far, there are no methods to unambiguously determine the structure and composition of a neural network based on the task description. In defense, I will say that for hardly-formalized tasks such a method will hardly ever be created. In addition, there are many different methods of network reduction (for example, OBD [1]), as well as various heuristics and rules of thumb. One of these rules says that the number of neurons in the hidden layer must be at least an order of magnitude greater than the number of inputs. If we take into account that the transformation from the image to the class indicator itself is quite complex and essentially nonlinear, you cannot do with a single layer. Based on the foregoing, we roughly estimate that the number of neurons in the hidden layers will be about 15,000 (10,000 in the 2nd layer and 5,000 in the third). At the same time, for a configuration with two hidden layers, the number of configured and trained links will be 10 million between the inputs and the first hidden layer + 50 million between the first and second + 50 thousand between the second and the output, if we assume that we have 10 outputs, each of which denotes a number from 0 to 9. Total roughly 60 million links . I knowingly mentioned that they are customizable - this means that when training for each of them it will be necessary to calculate the error gradient.
Well, it's okay, what can you do here, the
')
3. Convolutional neural networks
A solution to this problem was found by American scientist of French origin, Jan LeCoun , inspired by the works of Nobel laureates in the field of medicine Torsten Nils Wiesel and David H. Hubel . These scientists investigated the cat's visual cortex and found that there are so-called simple cells that are particularly responsive to straight lines from different angles and complex cells that react to the movement of lines in one direction. Jan LeKun proposed the use of so-called convolutional neural networks [2].
The idea of convolutional neural networks is the alternation of convolutional layers (C-layers), subsampling layers (S-layers) and the presence of fully connected (F-layers) layers at the output.

This architecture has 3 main paradigms:
- Local perception.
- Shared weight.
- Subsampling.
Local perception implies that not all of the image (or outputs of the previous layer) is fed to the input of one neuron, but only some of its area. This approach allowed us to maintain the topology of the image from layer to layer.
The concept of shared weights suggests that for a large number of links a very small set of weights is used. Those. if we have an image with the size of 32x32 pixels at the input, then each of the neurons of the next layer will receive only a small section of this image, for example, 5x5, and each of the fragments will be processed with the same set. It is important to understand that the sets of scales themselves can be many, but each of them will be applied to the entire image. Such kits are often called kernels. It is easy to calculate that even for 10 cores 5x5 in size for an input image 32x32 in size, the number of links will be approximately 256,000 (compare with 10 million), and the number of adjustable parameters is only 250!
And what, you ask, will this affect the quality of recognition? Oddly, for the better. The fact is that such an artificially imposed weight limit improves the generalizing properties of the network (generalization), which ultimately has a positive effect on the network's ability to find invariants in the image and react mainly to them, without paying attention to other noise. You can look at this approach a bit from the other side. Those who are engaged in image recognition classics and know how it works in practice (for example, in military technology) know that most of such systems are built on the basis of two-dimensional filters. The filter is a matrix of coefficients, usually manually defined. This matrix is applied to the image using a mathematical operation called convolution . The essence of this operation is that each image fragment is multiplied by the convolution matrix (core) element by element and the result is summed up and written to the similar position of the output image. The main property of such filters is that the value of their output is the greater, the more a fragment of the image is similar to the filter itself. Thus, the image is minimized with a certain core and it will give us a different image, each pixel of which will mean the degree of similarity of a fragment of the image to the filter. In other words, it will be a feature map.
The process of propagation of the signal in the C-layer, I tried to depict in the figure:

Each fragment of the image is multiplied element by element by a small matrix of weights (the core), the result is summed up. This sum is the pixel of the output image, which is called the attribute map. Here I omitted the fact that the weighted sum of inputs is still passed through the activation function (as in any other neural network). In fact, this can happen in the S-layer, there is no fundamental difference. It should be said that, ideally, not different fragments pass sequentially through the core, and in parallel the entire image passes through identical nuclei. In addition, the number of cores (sets of weights) is determined by the developer and depends on how many signs you need to select. Another feature of the convolutional layer is that it slightly reduces the image due to edge effects.
The essence of subsampling and S-layers is to reduce the spatial dimension of the image. Those. the input image is roughly (averaged) reduced by a specified number of times. Most often, 2 times, although there may be a non-uniform change, for example, 2 vertically and 3 horizontally. Subsampling is necessary to ensure scale invariance.
The alternation of layers allows mapping of features from feature maps, which in practice means the ability to recognize complex feature hierarchies.
Usually, after passing through several layers, the feature map degenerates into a vector or even a scalar, but there are hundreds of such feature maps. In this form, they are fed to one or two layers of a fully connected network. The output layer of such a network can have various activation functions. In the simplest case, this may be a tangential function, and radial basis functions are also successfully used.
4. Training
In order to start learning our network, you need to decide how to measure the quality of recognition. In our case, for this we will use the most common in the theory of neural networks the function of mean square error (MSE) [3]:
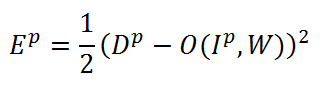
In this formula, Ep is a recognition error for the p-th training pair, Dp is the desired network output, O (Ip, W) is the network output, depending on the p-th input and weighting factors W, which include convolution kernels, displacements, weighting coefficients of S- and F-layers. The task of training is to adjust the weights W so that they give the minimal error Ep for any training pair (Ip, Dp). To calculate the error for the entire training sample, simply take the arithmetic average for errors for all training pairs. This average error is denoted by E.
To minimize the error function Ep, gradient methods are most effective. Consider the essence of gradient methods on the example of the simplest one-dimensional case (that is, when we have only one weight). If we decompose the error function Ep into the Taylor series, we get the following expression:
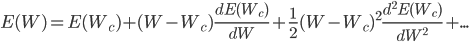
Here E is the same error function, Wc is some initial value of the weight. From school mathematics we remember that in order to find the extremum of a function, it is necessary to take its derivative and equate to zero. So let's do it, take the derivative of the error function with respect to weights, rejecting terms higher than 2nd order:
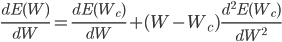
it follows from this expression that the weight at which the value of the error function will be minimal can be calculated from the following expression:
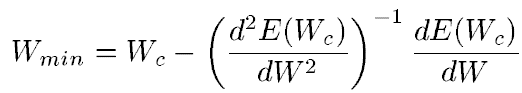
Those. the optimal weight is calculated as the current minus the derivative of the error function by weight divided by the second derivative of the error function. For the multidimensional case (i.e., for the weights matrix), everything is exactly the same, only the first derivative turns into a gradient (the vector of partial derivatives), and the second derivative turns into a Hessian (the matrix of the second partial derivatives). And here there are two options. If we omit the second derivative, we obtain an algorithm for the fastest gradient descent. If we still want to take into account the second derivative, we will be stunned by how many computing resources we need to calculate the full Hessian, and then also draw it. Therefore, usually the Hessian is replaced by something more simple. For example, one of the most well-known and successful methods, the Levenberg-Marquardt (LM) method, replaces the Hessian with its approximation using the Jacobian quadratic. Details here will not tell.
But what is important for us to know about these two methods is that the LM algorithm requires processing the entire training sample, whereas the gradient descent algorithm can work with each individual training sample. In the latter case, the algorithm is called a stochastic gradient. Given that our database contains 60,000 training samples, the stochastic gradient is more suitable for us. Another advantage of the stochastic gradient is that it is less susceptible to falling into a local minimum compared to LM.
There is also a stochastic modification of the LM algorithm, which I may mention later.
The presented formulas make it easy to calculate the error derivative with respect to weights located in the output layer. The error in hidden layers can be calculated using the widely known method of back propagation of errors in AI.
5. Implementation
Personally, I use to implement various algorithms, from which Matlab does not require real-time operation. This is a very convenient package whose M-language allows you to focus on the algorithm itself without worrying about memory allocation, I / O operations, etc. In addition, many different toolboxes allow you to create truly interdisciplinary applications in the shortest possible time. For example, using the Image Acquisition Toolbox, you can connect a webcam, use the Image Processing Toolbox to process the image from it, use the Neural Network Toolbox to form the robot's trajectory, and use the Virtual Reality Toolbox and Control Systems Toolbox to simulate the robot's movement. Speaking of the Neural Network Toolbox, this is a fairly flexible set of tools that allows you to create many neural networks of various types and architectures, but, unfortunately, not convolutional NA. It's all about shared scales. In the NN toolbox, the ability to specify shared weights is missing.
To eliminate this drawback, I wrote a class that allows you to implement the SNA of an arbitrary architecture and apply them to various tasks. Download the class here . The class itself was written so that the one who uses it has the maximum visible network structure. Everything is very abundantly commented, did not save on the name of variables. Network simulation speed is not bad and is a fraction of a second. The learning rate is not yet high (> 10 hours), but stay tuned, in the near future we plan to accelerate by orders of magnitude.
Who is interested in the implementation of SNS in C ++, can find it here and here .
6. Results
In the program on matlabcentral, a file of an already trained neural network is attached, as well as a GUI for demonstrating the results of work. The following are examples of recognition:


The link has a table of comparison of recognition methods based on MNIST. The first place is behind convolutional neural networks with the result of 0.39% recognition errors [4]. Most of these images are mistakenly recognized not every person correctly recognizes. In addition, elastic distortions of the input images were used in [4], as well as preliminary training without a teacher. But about these methods as in some other article.
References
- Yann LeCun, JS Denker, S. Solla, RL Howard and LD Jackel: Optimal Brain Damage, in Touretzky, David (Eds), Advance in Neural Information Processing Systems 2 (NIPS * 89), Morgan Kaufman, Denver, CO, 1990
- Y. LeCun and Y. Bengio: Convolutional Networks for Images, Speech, and Time-Series, in Arbib, MA (Eds), The Handbook of Brain Theory and Neural Networks, MIT Press, 1995
- Y. LeCun, L. Bottou, G. Orr and K. Muller: Efficient BackProp, in Orr, G. and Muller K. (Eds), Neural Networks: Tricks of the Trade, Springer, 1998
- Ranzato Marc'Aurelio, Christopher Poultney, Sumit Chopra and Yann LeCun: An Efficient Learning of Sparse Representations with an Energy-Based Model in J. Platt et al. (Eds), Advances in Neural Information Processing Systems (NIPS 2006), MIT Press, 2006
PS Thank you all for the comments and feedback. This is my first article on Habré, so I will be happy to see suggestions, comments, additions.
Source: https://habr.com/ru/post/74326/
All Articles