(Evil) use of C # 4.0 Dynamic - Typeless Lambda Calculus, Church Numerals, and all-all-all ... (part 1)

Introduction

Sunday morning, time for another episode in the Mad Resurrection series. Once again in the same category with the risk of brain rupture , but that’s just what we like, isn't it? This time we will look at typeless lambda calculus in C #. But hey, isn't C # a typed language? Really. But does this mean that everything you do in C # should be statically typed? Not necessarily: typing is present in the language as a tool that you can either not touch or use. In this topic, we will look at how the new dynamic keyword from C # 4.0 is at a somewhat strange angle ...

Sometimes types become obstacles on the way: maybe something is initially untyped (like XML documents without a schema, web services without a WSDL contract, etc.) or it is implied that this is something dynamically typed (like objects coming from dynamic languages). like Ruby or Python). And finally, the notorious APIs that do not adhere to their types: at some point you have static typing, but in the end you come to the fact that you have System.Object wherever possible (as an interaction between COM libraries of MS Office). For all these cases, dynamic C # 4.0 is exactly what is supposed to be. A classic example is to illustrate this feature, to tell about the IronPython object from C #. First definition in Python:

class Calc:
def Add(self, a, b):
return a + b
def GetCalc():
return Calc()

* This source code was highlighted with Source Code Highlighter .

The most beautiful thing about this Python calculator is its ability to work with everything that the addition operator supports. In other words, we can feed him two integer objects or two strings, or even a DateTime and TimeSpan. To make these calls, we use the dynamic keyword in C #:

var py = Python.CreateEngine();
dynamic script = py.ImportModule( "Calc" );
dynamic calc = script.GetCalc();
int three = calc.Add(1, 2);

* This source code was highlighted with Source Code Highlighter .

Ignore a few technical lines for downloading a python file; here the most important is the fact that the type of the variable calc is described as dynamic, which means all operations called from it will be allowed at runtime:
')


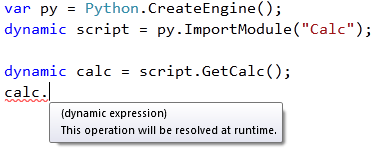
I will not go into details of how this works, maybe another time (outside the subject of insane Sunday topics), but this is the essence of this opportunity. Instead, we will do something in the style of “do not try to repeat it at home”: we will introduce a typeless lambda calculus .

Typeless lambda calculus as it is

The typeless lambda calculus, developed by Alonzo Church around 1930, is a theory about the computational aspects of functions. She considers functions as rules and defines two friendly operations to work with them: abstraction and application. In essence, this is all, but nevertheless, the theory has created a huge space for research. To convince you of this, I suggest you look at the number of pages in this book in your favorite online bookstore:



( comment of the translator: not so much: 621, see books.google.com.ua/books?id=ZdydJZVue50C&dq=the+lambda+calculus+its+syntax+and+semantics&hl=ru&source=gbs_navlinks_s )

So let me summarize the main things, quoting / paraphrasing the book above. First, we must define the concept of the λ -term:



As a typical exercise, bring out the fourth lambda term in the examples from its fully bracketed and bloated form.

Wherever there are lambda terms, they can be designated by functions, just as it is done in C # using lambda expressions. For example, the second example above is a function with argument “x”, which returns “x”. In other words, it is the identity function. However, she has no type: she can operate with anything (in particular, other lambda terms). In C #, we can write it like this:

Func <T, T> I = x => x;

where T stands for generic parameter. Obviously, this function can operate on values, but it can also operate on functions well: by taking a function, it will return exactly the same function:

I (5) // produces 5
I (I) // produces I

In fact, the next three examples above are closed terms, in the sense that all the symbols used in their “function body” (the part after the point) are in the “scope of action” by abstraction (s) above them. We call them combinators:



The last term in the previous example is not closed: it returns an “x” that was not abstracted out. This reflects the concept of a closure that we have in C #:

R x = ...;
Func <T, R> f = z => x;

Now we will no longer go into this, but suffice it to say that such beautiful words as “closure” are deeply rooted in the theoretical foundations. Consider yourself lucky that you happened to work with a language that lies on such solid theoretical grounds :-).

Next, we need the concept of free variables . In short, it will allow us to identify those variables that are not introduced by abstraction in this term. This definition is extremely simple:



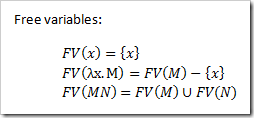
For combinators, the set of free variables will be empty. In contrast, for our last example (one result in a closure), the set will contain only one “x”. Nothing unimaginable, right?

And finally, now we can determine how the application is curried, based on the substitution :



To avoid name intersections (which can formally be prevented by using the variable naming convention by applying FV (free variables) above), we will be as careful as possible in naming variables. We all know this from C # and this is just a theoretical basis for visibility zones:

Func <T, T> I1 = x => x;

and

Func <T, T> I2 = y => y;

in fact, they are "the same." It’s a dangerous business to use such big words in the context of the entire runtime environment (CLR) and language (C #).

I do not claim that I1 and I2 refer to the same delegate: there is no identification between delegates who say that "x => x" and "y => y" are the same. Rather, I point out here that the I1 and I2 environments will be the same when applied to the same object. In lambda calculus, this refers to alpha transformations.

So far, ignoring the important problem of name conflicts, let's take a closer look at the above “beta-conversion” rule. The idea is simple: “the application of abstraction with another term results in a substitution”. This is almost the same as calling delegates in C #, but still with some differences: in the world of lambda calculus, substitution is nothing more than a mechanical rewriting of terms. In languages ​​like C #, the code is compiled as is and the delegate’s call does not magically rewrite the delegate’s body on the fly. But even more importantly, in C # we are directly interested in the semantics of call by value: before the call, the arguments must be brought to the “value” that can be passed to the call (via the delegates call mechanism).

Untyped or universally typed? (Untyped or uni-typed?)

And now the question of today: can we typify (in the sense of the CLR / C # type system) all lambda terms? It seems like we did it with the combinator I, expressing it as Func <T, T> using generalizations (generics): passing the value of a particular type T, the result is the same value and exactly the same type. In fact, how about inferring such signatures? C # does not do this, but F # can (Höndley – Milner type deduction, as is usually done in ML-shaped languages):



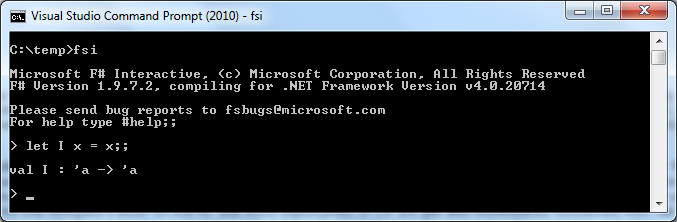
Okay, "I" is derived to the type to be the type that goes from 'a to' a, where 'a is the notation for a generic parameter. What about K, a combinator that takes two arguments and always returns the first one (the parent of the "constant" value):



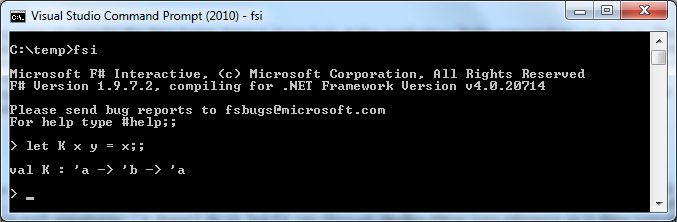
It seems that we are still making good progress. F # brought out the type that should be "'a to' b to 'a". Wow, what's going on here? In C #, it would look like Func <T1, Func <T2, T1 >>: a function that takes an argument of type T1 returns a function that takes an argument of type T2 and returns a value of type T1. Do you get it? What happened here is called “currying, when a function with n arguments turns into nested functions that serve one argument at a time. This means that we can write, for example, “K 5”, to create a new function that eats the remaining “y” argument (of any type) and always returns 5.
Even for such a (relatively) complex beast as S, the type can be inferred:



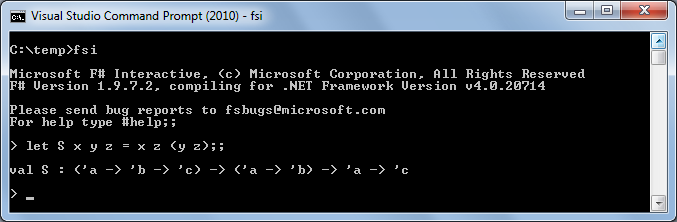
Impressive? Actually not so difficult. Now see how we ourselves derive the type from the function body. First of all, we see x in front of two terms: „z“ and “(yz)“. This means “x” is a function with two arguments and it is assumed that it returns something. Assign the type names for these things: the first argument "z" takes type 'a and the result from "(yz)" is type' b. The result we write as' c. In other words, the type "x" is inferred as' a -> 'b ->' c. Next, we need to output the type "y", based on our initial type identification for "(yz)", as' b. We see that “y” is a function with one argument, “z”. We have already defined the type “z” as' a, so that the type “y“ takes the form 'a ->' b. Finally, our function “S” also takes “z” as the third argument, which is typed as' a. Now, if this is all combined with the returned type "x", then we get the signature shown above.

Well, it looks like we can type all lambda terms, right? Unfortunately not. Here is the proof:



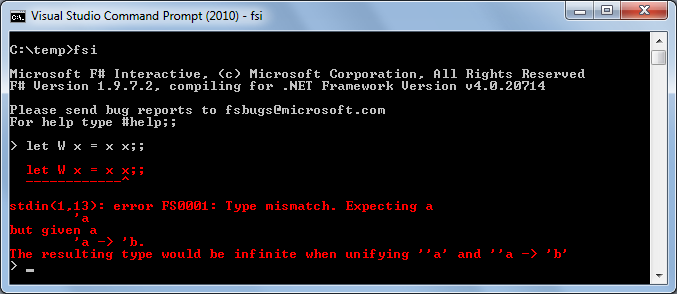
Here I wrote a function W, which the resulting argument x applies to itself. Such a simple lambda term and you can not find a type for it. Join me in this exercise for the brain: W takes one argument x, say, type 'a. Now, x applies to x. From here it seems that x is a function with one argument. This argument is x, which we have already typed as' a. How about a return type? Let's call it 'b, so now we have come to the conclusion that x should be of the type' a -> 'b, which is not the same as' a, as we had before: unification failed.

This is where the difference between typeless lambda calculus and type variants (like typed lambda calculus and generalizations and something else called “System F”). C #, being a typed language, does not allow us to get rid of types in general, so that we are not able to get something "untyped." But what about “universally typed” (thanks to Robert Harper): replace all types with one single type. Can we do this? Answer: with „dynamic“ we can do it!
dynamic W = new Func <dynamic, dynamic> (x => x (x));

Unfortunately, we actually need a partly ugly call to the delegate constructor, but notice how we assign the type “dynamic -> dynamic” to “dynamic” on the left. In other words, we interpret all (non-functional values ​​and functional "objects") as dynamic. The code above compiles just fine, but how does the x (x) work in the body of the lambda? Well, at runtime, the system will figure out what type x is and will check that it can be called as a unary function. For example:

dynamic W = new Func<dynamic, dynamic>(x => x(x));
W(1);

* This source code was highlighted with Source Code Highlighter .

This is clearly a bad decision. It corresponds to the “function call integer 1” with the argument “integer 1”. It is clear that the integer value cannot be used as a function (this is good!) So the runtime will return:

Unhandled Exception: Microsoft.CSharp.RuntimeBinder.RuntimeBinderException: Cannot invoke a non-delegate type
at CallSite.Target(Closure , CallSite , Object , Object )
at System.Dynamic.UpdateDelegates.UpdateAndExecute2[T0,T1,TRet](CallSite site, T0 arg0, T1 arg1)
at UntypedLambda.Program.b__46(Object x)
at CallSite.Target(Closure , CallSite , Object , Int32 )
at System.Dynamic.UpdateDelegates.UpdateAndExecuteVoid2[T0,T1](CallSite site, T0 arg0, T1 arg1)
at UntypedLambda.Program.Main()

, , DLR , .
?

var I = new Func<dynamic, dynamic>(x => x);
dynamic W = new Func<dynamic, dynamic>(x => x(x));
Console .WriteLine(W(I)(42));

* This source code was highlighted with Source Code Highlighter .

. I W, I(I), ( -) I. 42, 42.

… , dynamic
. - Scheme? , :-).

:
, :
SKI combinators
Church Booleans
Church Numerals
Going nuts - recursive functions

Unhandled Exception: Microsoft.CSharp.RuntimeBinder.RuntimeBinderException: Cannot invoke a non-delegate type
at CallSite.Target(Closure , CallSite , Object , Object )
at System.Dynamic.UpdateDelegates.UpdateAndExecute2[T0,T1,TRet](CallSite site, T0 arg0, T1 arg1)
at UntypedLambda.Program.b__46(Object x)
at CallSite.Target(Closure , CallSite , Object , Int32 )
at System.Dynamic.UpdateDelegates.UpdateAndExecuteVoid2[T0,T1](CallSite site, T0 arg0, T1 arg1)
at UntypedLambda.Program.Main()

, , DLR , .
?

var I = new Func<dynamic, dynamic>(x => x);
dynamic W = new Func<dynamic, dynamic>(x => x(x));
Console .WriteLine(W(I)(42));

* This source code was highlighted with Source Code Highlighter .

. I W, I(I), ( -) I. 42, 42.

… , dynamic
. - Scheme? , :-).

:
, :
SKI combinators
Church Booleans
Church Numerals
Going nuts - recursive functions

Unhandled Exception: Microsoft.CSharp.RuntimeBinder.RuntimeBinderException: Cannot invoke a non-delegate type
at CallSite.Target(Closure , CallSite , Object , Object )
at System.Dynamic.UpdateDelegates.UpdateAndExecute2[T0,T1,TRet](CallSite site, T0 arg0, T1 arg1)
at UntypedLambda.Program.b__46(Object x)
at CallSite.Target(Closure , CallSite , Object , Int32 )
at System.Dynamic.UpdateDelegates.UpdateAndExecuteVoid2[T0,T1](CallSite site, T0 arg0, T1 arg1)
at UntypedLambda.Program.Main()

, , DLR , .
?

var I = new Func<dynamic, dynamic>(x => x);
dynamic W = new Func<dynamic, dynamic>(x => x(x));
Console .WriteLine(W(I)(42));

* This source code was highlighted with Source Code Highlighter .

. I W, I(I), ( -) I. 42, 42.

… , dynamic
. - Scheme? , :-).

:
, :
SKI combinators
Church Booleans
Church Numerals
Going nuts - recursive functions