L-Systems - the mathematical beauty of plants
The beauty of plants has attracted the attention of mathematicians for centuries. Interesting geometric properties of plants, such as the symmetry of the leaves relative to the central axis, the radial symmetry of flowers, and the spiral arrangement of the seeds in the cones, were most actively studied. “Beauty is associated with symmetry” (H. Weyl. Symmetry). During the growth of living organisms, especially plants, one can clearly see regularly repeated multicellular structures. In the case of compound leaves, for example, small leaves, which are part of a large adult leaf, have the same shape that the whole leaf had at an early stage of formation.
In 1968 Hungarian biologist and botanist Aristid Lindenmayer (Aristid Lindenmayer) proposed a mathematical model to study the development of simple multicellular organisms, which was later expanded and used to model complex branching structures - various trees and flowers. This model is called the Lindenmayer System, or simply the L-System.
For those who are in the subject and do not want to read everything in their entirety, check down, there is a question.
I will shorten the L-System to L in the text.
')
The main idea of L is the constant rewriting (rewriting) of line elements. What is it about? In short, rewriting is a way to get complex objects by replacing parts of a simple initial object according to some rules. A classic example is a snowflake. In the figure, initiator is the initial object whose faces are replaced by the generator. Next, the same thing is done with the new object. In this case, the usual fractal.

Returning to L and drawing an analogy with fractals, we can say that L operates on a string of characters according to special rules, starting with the original simple axiom. People familiar with the concept of grammar will immediately notice that in essence L is. But the fundamental difference between L and formal grammars is that the rules apply simultaneously to the whole line, to each character, plus, there are no concepts of terminal and non-terminal characters. That is, the "conclusion" of this grammar can continue indefinitely. The simultaneous application of the rules very quickly becomes clear when you consider where this model came from. In biology, each cell grows, divides and develops in parallel in time. The following picture shows the relationship between context-free (OL), context-dependent (IL) L and other formal grammars in the Chomsky hierarchy .

As in Chomsky’s classification, L have their own classification from simple to complex and powerful.
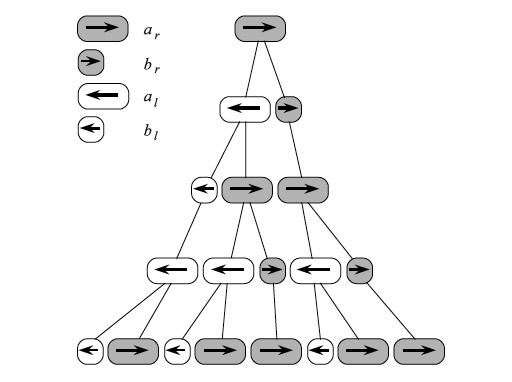
The simplest example is deterministic context-free L, or abbreviated DOL. I don’t like formal grammar definitions, so I’ll just say it in my own words. There is a set of symbols - the alphabet. This alphabet records the string with which L is working. There is an axiom — the original string of one or more letters and a set of rules of the form a → ab. During each iteration of the algorithm, applying a rule to a letter from the current line, it (the letter) is replaced with a set of letters to the right of the arrow. It is easier to consider a specific example of the development of the multicellular organism Anabaena catenula, which Lindenmeier studied when he proposed the model L.
Let our alphabet consist of the following symbols, each of which denotes a certain cell: a a a r b l b r .
Axiom consists of one symbol.
ω: a r
And 4 rules.
p1: a r → a l b r
p2: a l → b l a r
p3: b r → a r
p4: b l → a l
The rules tell which symbols change to which ones during the growth of the organism. The picture shows how applying the rules we observe the "division" of cells and development.
So far we have seen how to draw a one-dimensional bacterium, but with the help of the well-known children's programming language LOGO , in which it is proposed to control the turtle and draw shapes on the screen, one can already draw two-dimensional and three-dimensional fractals and repeating structures. How? It's simple. Take the alphabet, in which each character means a certain command for a two-dimensional or three-dimensional bug:
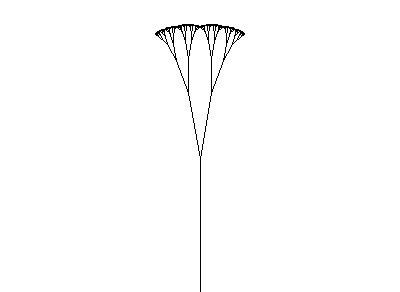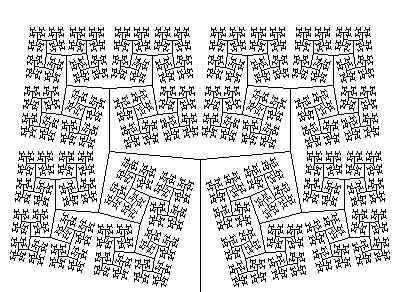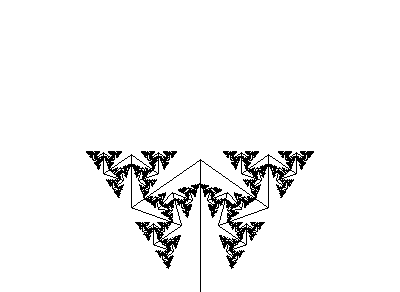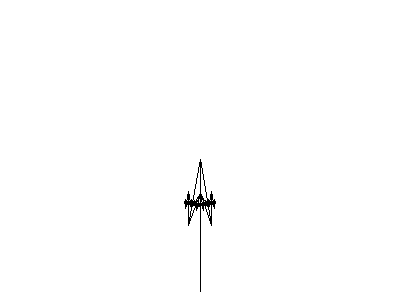
These commands use the default values of the rotation angle δ, the step length and the basis vectors of two-dimensional and three-dimensional space. Examples of two-dimensional fractals and L generating them can be seen in the following picture.

Everything that was before is, in general, continuous curves. Of course, it is thus very difficult to model plants with their branching topology. To do this, the symbols [and] were added to the alphabet, which indicate the beginning and end of branching, respectively. When the turtle encounters the symbol [, its current state is written to the stack and pulled out when the symbol is encountered].
Already such a simple grammar can generate quite interesting two-dimensional and three-dimensional objects similar to trees.

Of course, science did not stand still, and now we have a solid hierarchy of L starting from the simple DOL considered earlier.
Stochastic L.
Stochastic L add the ability to specify the probability of the fulfillment of a rule, and in the general case are not deterministic, because different rules may have the same symbol to the left. This introduces some element of randomness into the resulting structures.
Context-dependent L.
As well as context dependence in formal grammars, in L the syntax of the rules is complicated and takes into account the environment of the replaced character.
Parametric L.
A variable parameter (possibly more than one) is added to each symbol, which allows, for example, specifying the rotation angle for + and -, the stride length and line thickness, checking the conditions for applying the rule, counting the number of iterations and transmitting the “signals” back and forth. An example of a parametric L.
Parametric context-dependent L models allow the growth of multicellular organisms and plants, taking into account biochemical processes and the environment. For example, our old friend Anabaena catenula in a more complex form. An example from the book [1].
As written in the book, this bacterium consists of two types of cells: vegetative cells and heterocysts . Usually, vegetative cells are divided into two similar vegetative cells. However, in some cases, vegetative cells are converted to heterocyst. Their distribution follows a well-observable pattern, in which neighboring heterocysts are separated by approximately the same number of vegetative cells. But how does the body maintain a constant distance between the heterocysts during growth? The proposed model describes this phenomenon in terms of biology. It is assumed that the location of the heterocysts is regulated by nitrogen compounds produced by these cells, which are transferred to other cells of the body and consumed in vegetative cells. If the content of these compounds in the young vegetative cell falls below a certain level, this cell turns into a heterocyst.
The L-System below simulates the growth of a bacterium with this in mind.
#define assigns values to the constants used in L.
#include loads a heterocyst form, in this case a circle.
The cells are represented by the F (s, t, c) module, where s is the cell length, t is the cell type (0 is heterocyst, 1 and 2 are vegetative cells), and c is the nitrogen concentration.

For example, the recent hypno-lab that conquered the Internet is essentially a combination of the simplest L.
This is just a superficial description of the theory and small examples of practical application. What awaits the curious researcher next?
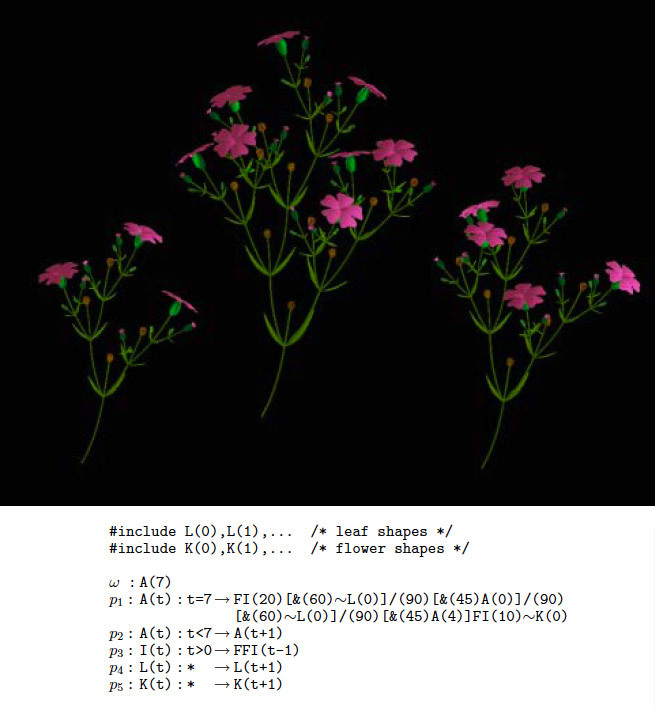


Back in the late 80s, L was used to visualize plant models. Now the possibilities of computers are far ahead. Many games and 3d modeling tools use procedural content generation, including L-Systems. As you can see, from a set of simple rules you can get a huge number of different plants and plant whole fields with them.
From the editors I use L myself in Houdini , I heard that there are plugins for other packages. The so-called Virtual Lab allows you to experiment and animate L.
Methods of using grammars are also used in the so-called Shape Grammars , but more on that later.
Some posts on the Internet.
http://avalter.blogspot.com/2009/08/2d-l.html
Generally speaking, the only available book is The Algorithmic Beauty of Plants . Also, on the Internet are scattered old random articles. More or less new can be found on springerlink.com for a lot of money or in the institute library for free.
What can I say, the material is quite small.
I myself have exactly nothing to do with biology, but I am a Master of Mathematics with a few innocent hobbies. But I really like the idea of L-Systems. Simplicity with great features. Once upon a time I wondered how DNA contains complete information about me. How can you shove all the information about all the cells into each cell? But in any way, one might say, the theory L opened my eyes! It is not written in my DNA how I look, but how to collect me (in general terms). Something similar to the set of rules in L, only related to protein synthesis.
A simple model so clearly describes our life with you.
Further more, we transform the rules into “DNA” and grow virtual multicellular by genetic algorithm.
I would like to find people who are also interested in the scientific component of L, to share materials and articles. It so happened that I am currently working on the upgraded concept of L-Systems, but I have not had the opportunity to see what has been written on this topic over the past five years. I do not want to reinvent the wheel.
Contact the author of the BOOK failed, the answering machine says that he left for the Sabbath until January (8
Also, I am looking for information on Shape Grammars for 3d modeling. There is a task to generate from the parameters of the spacecraft, well, you know such huge things with a bunch of small details - ideal candidates for SG. Do you have to write a plugin for Houdini in Python?
In 1968 Hungarian biologist and botanist Aristid Lindenmayer (Aristid Lindenmayer) proposed a mathematical model to study the development of simple multicellular organisms, which was later expanded and used to model complex branching structures - various trees and flowers. This model is called the Lindenmayer System, or simply the L-System.
For those who are in the subject and do not want to read everything in their entirety, check down, there is a question.
I will shorten the L-System to L in the text.
')
Rewriting.
The main idea of L is the constant rewriting (rewriting) of line elements. What is it about? In short, rewriting is a way to get complex objects by replacing parts of a simple initial object according to some rules. A classic example is a snowflake. In the figure, initiator is the initial object whose faces are replaced by the generator. Next, the same thing is done with the new object. In this case, the usual fractal.

Returning to L and drawing an analogy with fractals, we can say that L operates on a string of characters according to special rules, starting with the original simple axiom. People familiar with the concept of grammar will immediately notice that in essence L is. But the fundamental difference between L and formal grammars is that the rules apply simultaneously to the whole line, to each character, plus, there are no concepts of terminal and non-terminal characters. That is, the "conclusion" of this grammar can continue indefinitely. The simultaneous application of the rules very quickly becomes clear when you consider where this model came from. In biology, each cell grows, divides and develops in parallel in time. The following picture shows the relationship between context-free (OL), context-dependent (IL) L and other formal grammars in the Chomsky hierarchy .

The most simple L-Systems.
As in Chomsky’s classification, L have their own classification from simple to complex and powerful.
The simplest example is deterministic context-free L, or abbreviated DOL. I don’t like formal grammar definitions, so I’ll just say it in my own words. There is a set of symbols - the alphabet. This alphabet records the string with which L is working. There is an axiom — the original string of one or more letters and a set of rules of the form a → ab. During each iteration of the algorithm, applying a rule to a letter from the current line, it (the letter) is replaced with a set of letters to the right of the arrow. It is easier to consider a specific example of the development of the multicellular organism Anabaena catenula, which Lindenmeier studied when he proposed the model L.
Let our alphabet consist of the following symbols, each of which denotes a certain cell: a a a r b l b r .
Axiom consists of one symbol.
ω: a r
And 4 rules.
p1: a r → a l b r
p2: a l → b l a r
p3: b r → a r
p4: b l → a l
The rules tell which symbols change to which ones during the growth of the organism. The picture shows how applying the rules we observe the "division" of cells and development.

Turtle interpretation of strings.
So far we have seen how to draw a one-dimensional bacterium, but with the help of the well-known children's programming language LOGO , in which it is proposed to control the turtle and draw shapes on the screen, one can already draw two-dimensional and three-dimensional fractals and repeating structures. How? It's simple. Take the alphabet, in which each character means a certain command for a two-dimensional or three-dimensional bug:
- F - move forward and draw a line
- f - go ahead without drawing anything
- + - turn left
- - - turn right
- & - turn down
- ^ - turn up
- \ - lean to the left
- / - lean to the right
- | - turn 180 degrees
These commands use the default values of the rotation angle δ, the step length and the basis vectors of two-dimensional and three-dimensional space. Examples of two-dimensional fractals and L generating them can be seen in the following picture.

Plants and branching structures.
Everything that was before is, in general, continuous curves. Of course, it is thus very difficult to model plants with their branching topology. To do this, the symbols [and] were added to the alphabet, which indicate the beginning and end of branching, respectively. When the turtle encounters the symbol [, its current state is written to the stack and pulled out when the symbol is encountered].
Already such a simple grammar can generate quite interesting two-dimensional and three-dimensional objects similar to trees.

More sophisticated grammar.
Of course, science did not stand still, and now we have a solid hierarchy of L starting from the simple DOL considered earlier.
Stochastic L.
Stochastic L add the ability to specify the probability of the fulfillment of a rule, and in the general case are not deterministic, because different rules may have the same symbol to the left. This introduces some element of randomness into the resulting structures.
Context-dependent L.
As well as context dependence in formal grammars, in L the syntax of the rules is complicated and takes into account the environment of the replaced character.
Parametric L.
A variable parameter (possibly more than one) is added to each symbol, which allows, for example, specifying the rotation angle for + and -, the stride length and line thickness, checking the conditions for applying the rule, counting the number of iterations and transmitting the “signals” back and forth. An example of a parametric L.
ω : B(2)A(4, 4)
p1 : A(x, y) :y <= 3 → A(x ∗ 2, x + y)
p2 : A(x, y) :y > 3 → B(x)A(x/y, 0)
p3 : B(x) :x < 1 → C
p4 : B(x) :x >= 1 → B(x − 1)Parametric context-dependent L models allow the growth of multicellular organisms and plants, taking into account biochemical processes and the environment. For example, our old friend Anabaena catenula in a more complex form. An example from the book [1].
As written in the book, this bacterium consists of two types of cells: vegetative cells and heterocysts . Usually, vegetative cells are divided into two similar vegetative cells. However, in some cases, vegetative cells are converted to heterocyst. Their distribution follows a well-observable pattern, in which neighboring heterocysts are separated by approximately the same number of vegetative cells. But how does the body maintain a constant distance between the heterocysts during growth? The proposed model describes this phenomenon in terms of biology. It is assumed that the location of the heterocysts is regulated by nitrogen compounds produced by these cells, which are transferred to other cells of the body and consumed in vegetative cells. If the content of these compounds in the young vegetative cell falls below a certain level, this cell turns into a heterocyst.
The L-System below simulates the growth of a bacterium with this in mind.
#define assigns values to the constants used in L.
#include loads a heterocyst form, in this case a circle.
The cells are represented by the F (s, t, c) module, where s is the cell length, t is the cell type (0 is heterocyst, 1 and 2 are vegetative cells), and c is the nitrogen concentration.
#define CH 900 /* high concentration */
#define CT 0.4 /* concentration threshold */
#define ST 3.9 /* segment size threshold */
#include H /* heterocyst shape specification */
#ignore f ∼ H
ω : -(90)F(0,0,CH)F(4,1,CH)F(0,0,CH)
p1 : F(s,t,c) : t=1 & s>=6 → F(s/3*2,2,c)f(1)F(s/3,1,c)
p2 : F(s,t,c) : t=2 & s>=6 → F(s/3,2,c)f(1)F(s/3*2,1,c)
p3 : F(h,i,k) < F(s,t,c) > F(o,p,r) : s>ST|c>CT → F(s+.1,t,c+0.25*(k+r-3*c))
p4 : F(h,i,k) < F(s,t,c) > F(o,p,r) : !(s>ST|c>CT) → F(0,0,CH) ∼ H(1)
p5 : H(s) : s<3 → H(s*1.1)
Hypnoqab
For example, the recent hypno-lab that conquered the Internet is essentially a combination of the simplest L.

#define R 1.456
ω : A(1)
p1 : A(s) → F(s)[+A(s/R)][−A(s/R)]More advanced.
This is just a superficial description of the theory and small examples of practical application. What awaits the curious researcher next?
- Modeling the growth of two-dimensional and three-dimensional multicellular organisms
- Tree Growth Animation
- Environmental Modeling
- Chemistry and biological processes modeling and growth functions
- L application to generate surfaces
- Other diverse uses, including for real estate and city modeling.
Examples




Using.
Back in the late 80s, L was used to visualize plant models. Now the possibilities of computers are far ahead. Many games and 3d modeling tools use procedural content generation, including L-Systems. As you can see, from a set of simple rules you can get a huge number of different plants and plant whole fields with them.
From the editors I use L myself in Houdini , I heard that there are plugins for other packages. The so-called Virtual Lab allows you to experiment and animate L.
Methods of using grammars are also used in the so-called Shape Grammars , but more on that later.
Some posts on the Internet.
http://avalter.blogspot.com/2009/08/2d-l.html
Books and additional material.
Generally speaking, the only available book is The Algorithmic Beauty of Plants . Also, on the Internet are scattered old random articles. More or less new can be found on springerlink.com for a lot of money or in the institute library for free.
What can I say, the material is quite small.
Okolobiologichesky thoughts.
I myself have exactly nothing to do with biology, but I am a Master of Mathematics with a few innocent hobbies. But I really like the idea of L-Systems. Simplicity with great features. Once upon a time I wondered how DNA contains complete information about me. How can you shove all the information about all the cells into each cell? But in any way, one might say, the theory L opened my eyes! It is not written in my DNA how I look, but how to collect me (in general terms). Something similar to the set of rules in L, only related to protein synthesis.
A simple model so clearly describes our life with you.
Further more, we transform the rules into “DNA” and grow virtual multicellular by genetic algorithm.
Scientific thoughts.
I would like to find people who are also interested in the scientific component of L, to share materials and articles. It so happened that I am currently working on the upgraded concept of L-Systems, but I have not had the opportunity to see what has been written on this topic over the past five years. I do not want to reinvent the wheel.
Contact the author of the BOOK failed, the answering machine says that he left for the Sabbath until January (8
Also, I am looking for information on Shape Grammars for 3d modeling. There is a task to generate from the parameters of the spacecraft, well, you know such huge things with a bunch of small details - ideal candidates for SG. Do you have to write a plugin for Houdini in Python?
Source: https://habr.com/ru/post/69989/
All Articles