Mixed AI in the game DROD - man + computer =?
DROD is a very unusual logic game. Its main features:
The heads are to kill all the monsters in the room 38x32 cells. The player controls a character who occupies 1 cage, who holds a sword that occupies another of the 8 neighboring cells. Each turn, you can either go to one of the 8 adjacent cells, or turn the sword, or wait. After which the surviving monsters take turns. If they can occupy the cage on which the player is standing, he loses and returns to the top of the room.
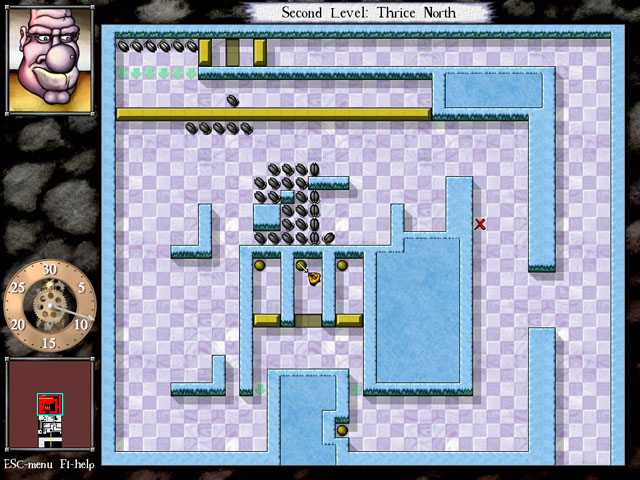
Additional interest in the game gives the table of records of speed (by the number of moves) of the passage of rooms. It is our goal. But how can you apply a computer to the game, with conceptually different puzzles and an astronomical number of options (at each moment we have 11 options for the move, and the total number of possible room states is much more than in chess) ?! There is only one way out - to shift the intellectual part of the task to the person, and the calculated part (optimization of the decision on the number of moves) to the computer.
')
When I started the task I did not hope for any success. In the end, rooms in DROD are so complex that you have to think about them for a month. But still I decided to take a chance.
The first thing that had to be done was to simplify the model of the game to increase the speed of the simulation of moves. Because of this simplification, many elements have to be replaced either with equivalent ones in this situation, or with similar ones, or only the solution of the puzzle part can be optimized. Secondly, we had to come up with a compact storage scheme for the state of the room and use an archiver plus it, otherwise the hard disk space disappears very quickly, and the IO speed noticeably affects the performance. After which the following simple search was written:
As the first evaluation function for the first room, the number of monsters in the room was chosen — the player's coordinate along the y axis (this is due to the specifics of the room). Imagine my surprise when after launching with only N = 100000 variants (I remind you that this corresponds to the number of variants somewhere after 5 moves, with a typical solution length of 300 moves) the program after several hours of work did not only manage to get through the room (more precisely its main part, after which to finish off the remaining monsters is easy), over which I unsuccessfully fought not the first day, but I did it almost 2 times faster than the best human solution for this room! As a result, the tandem "evaluation function, invented by me" + chooser could pass a very significant percentage of rooms. Only unsupported elements could stop it, rooms in which it is not possible to invent any reasonable evaluation function and trapdors (there is still “dirt” with which there is a similar problem) ...
Trapdor is a cell that you can stand on only once. As soon as you leave it, the trapdor falls down and emptiness is formed. Each trapdor increases the number of options in two, and if we consider that they usually fill in whole areas, then neither 10 ^ 5 nor 10 ^ 8 options help. The program begins to count many essentially the same options, among which, at one fine moment, the correct one does not turn out. It would seem a hopeless situation. So I thought, until I desperately needed to find a solution to such a room. It turned out that a simple modification of the algorithm solves the problem. In place of choosing the N best options in terms of the evaluation function f, you need to choose N best options in terms of random * exp (-const * f) (thanks to the annealing method for this idea), where const is determined by a person through a close look at the ceiling . Actually when const tends to infinity, we get the usual scheme of choice. However, as a board, the new method requires a more accurate selection of the evaluation function (previously, it was only the ordering on the state sets that the evaluation function f set was important, and now the values themselves are important). In the room I needed, this approach allowed me to find a good solution. Although it should be recognized that the general problem of the trapors remains unresolved, because often the topology of the remaining trapors is not important, which cannot be expressed as an evaluation function, and the use of randomness hurts the solution variants in which the degree of reasonable ramifications is not great.
- Stepping. Unlike supaplex, the reaction doesn't matter.
- Determination. There is no element of chance, any position can be calculated in the mind, although usually this is not very easy to do.
- Great conceptual variety of puzzles. Because of this, the game bothers much more slowly than, for example, Sudoku.
- Adventure entourage, giving meaning to the process (in the main mission, we make the virtual world DROD a little cleaner).
The heads are to kill all the monsters in the room 38x32 cells. The player controls a character who occupies 1 cage, who holds a sword that occupies another of the 8 neighboring cells. Each turn, you can either go to one of the 8 adjacent cells, or turn the sword, or wait. After which the surviving monsters take turns. If they can occupy the cage on which the player is standing, he loses and returns to the top of the room.

Additional interest in the game gives the table of records of speed (by the number of moves) of the passage of rooms. It is our goal. But how can you apply a computer to the game, with conceptually different puzzles and an astronomical number of options (at each moment we have 11 options for the move, and the total number of possible room states is much more than in chess) ?! There is only one way out - to shift the intellectual part of the task to the person, and the calculated part (optimization of the decision on the number of moves) to the computer.
')
When I started the task I did not hope for any success. In the end, rooms in DROD are so complex that you have to think about them for a month. But still I decided to take a chance.
The first thing that had to be done was to simplify the model of the game to increase the speed of the simulation of moves. Because of this simplification, many elements have to be replaced either with equivalent ones in this situation, or with similar ones, or only the solution of the puzzle part can be optimized. Secondly, we had to come up with a compact storage scheme for the state of the room and use an archiver plus it, otherwise the hard disk space disappears very quickly, and the IO speed noticeably affects the performance. After which the following simple search was written:
- We make all possible moves from the current set of positions. In this case, the same positions are removed using a hash table.
- Choose N best options for some evaluation function. (due to the discreteness of the values of the evaluation function, they may turn out to be slightly less than N)
- We print the best option and go back to the first step.
As the first evaluation function for the first room, the number of monsters in the room was chosen — the player's coordinate along the y axis (this is due to the specifics of the room). Imagine my surprise when after launching with only N = 100000 variants (I remind you that this corresponds to the number of variants somewhere after 5 moves, with a typical solution length of 300 moves) the program after several hours of work did not only manage to get through the room (more precisely its main part, after which to finish off the remaining monsters is easy), over which I unsuccessfully fought not the first day, but I did it almost 2 times faster than the best human solution for this room! As a result, the tandem "evaluation function, invented by me" + chooser could pass a very significant percentage of rooms. Only unsupported elements could stop it, rooms in which it is not possible to invent any reasonable evaluation function and trapdors (there is still “dirt” with which there is a similar problem) ...
Trapdor is a cell that you can stand on only once. As soon as you leave it, the trapdor falls down and emptiness is formed. Each trapdor increases the number of options in two, and if we consider that they usually fill in whole areas, then neither 10 ^ 5 nor 10 ^ 8 options help. The program begins to count many essentially the same options, among which, at one fine moment, the correct one does not turn out. It would seem a hopeless situation. So I thought, until I desperately needed to find a solution to such a room. It turned out that a simple modification of the algorithm solves the problem. In place of choosing the N best options in terms of the evaluation function f, you need to choose N best options in terms of random * exp (-const * f) (thanks to the annealing method for this idea), where const is determined by a person through a close look at the ceiling . Actually when const tends to infinity, we get the usual scheme of choice. However, as a board, the new method requires a more accurate selection of the evaluation function (previously, it was only the ordering on the state sets that the evaluation function f set was important, and now the values themselves are important). In the room I needed, this approach allowed me to find a good solution. Although it should be recognized that the general problem of the trapors remains unresolved, because often the topology of the remaining trapors is not important, which cannot be expressed as an evaluation function, and the use of randomness hurts the solution variants in which the degree of reasonable ramifications is not great.
Source: https://habr.com/ru/post/67913/
All Articles