Prologue

In continuation of the published article.

Compilers are probably one of the most interesting topics in system programming.
This article does not tell how to write an ideal, or at least working compiler, but it will help clarify a couple of aspects of its work, using the network topological sorting method.

What is a network?

The network is an infinite directed graph (The previous article dealt with the question of contours and methods for finding them).
For the algorithm, we need some properties, some of them were discussed in more detail in the very first article.


')
As can be seen from the picture, each vertex can be characterized by the number of arcs entering it ( half-degree of approach ), and the number of arcs emanating from it to other vertices ( half-degree of outcome ).
If a vertex has no incoming arc, the vertex is called a network source .
If the vertex has no outgoing arc, the vertex is called the network sink .



Consider the network on the example of the assembly application.
Files are denoted by vertices.
The role of arcs in the network is easier to understand from the picture:



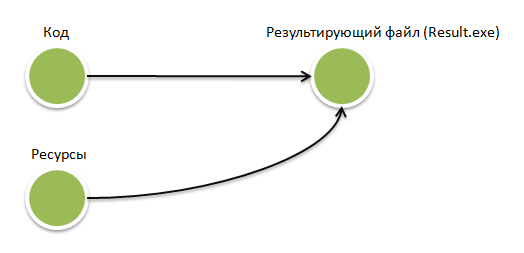
The arc going from the vertex “Code” to the vertex “Resulting file” means that the “Code” must be processed before Result.exe is received
Before a vertex can be processed, all vertices that reference it should be processed.

Everything seems simple when we see a drawn network of small size.
Let's move closer to reality and consider building a small program.

Example 1:


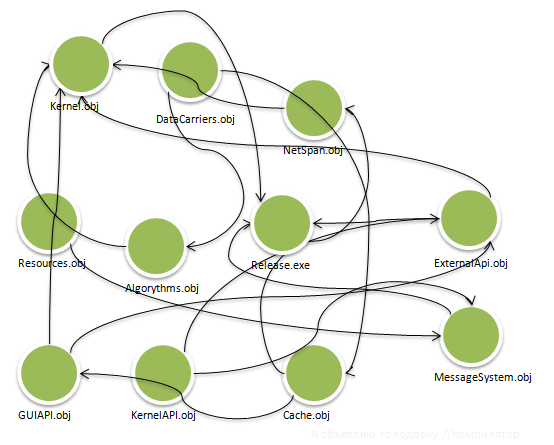
Unfortunately, even modern compilers are not so big-eyed in order to see here the correct build sequence.

Algorithm

How, then, does the compiler understand what to do first, and then what?
First, we describe what we want from our algorithm, and then we give the code.
So, our goal is to create a network consisting of several levels.



It can be seen from the figure that tasks within one level depend only on tasks at lower levels, and are independent of each other.
In this case, to achieve the goal, we first need to complete all tasks of level 0 in any order, then, in any order, tasks of level 1, etc., to level 3 (the last).

To solve the problem, we need the representation of the graph as a matrix (ij element = 1 if there is an arc from vertex i to vertex j, and is equal to 0 if there is no arc).

Consider another example.

Example 2:


In the row under the table, the semi-degrees of approach are given for all the vertices. Each number represents the sum of the units in the corresponding column of the matrix.

In the first step of the algorithm, we select all the vertices with a zero degree of approach, bring them to the zero level and, mentally, throw them out of the graph.



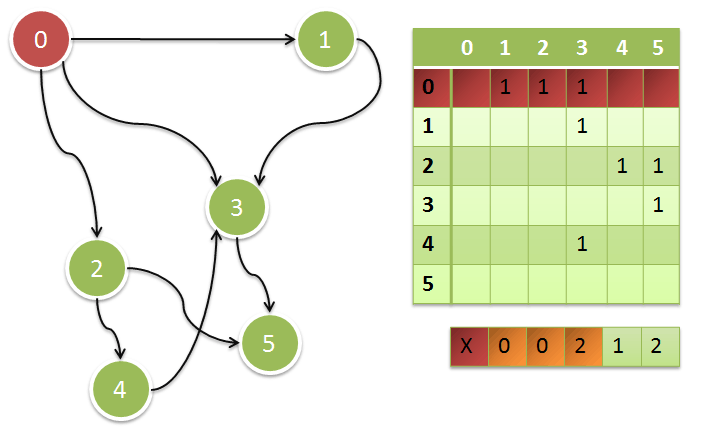
As a result, (we no longer take into account the rows of the matrix corresponding to the processed vertices), the half-degrees of the approach of the remaining vertices will decrease.

Next, we do the same with the remaining vertices with zero half degree of entry and place them in the first level:



Subsequent steps are similar.



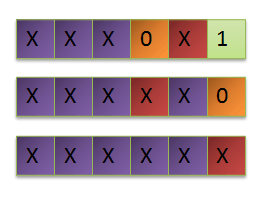
At the very beginning, we demanded that our graph be non-contour, thanks to this requirement, at each step we will have new peaks with a zero degree of approach.

Apply the algorithm to our network from example 1:

Implementation example

The basic framework that we need:

public class GraphNode
{
public List <GraphNode> LinkedNodes;
}

public class Graph
{
public List <GraphNode> nodes;

public void TopologicSort( out List < string > algResult, bool animated)
}

* This source code was highlighted with Source Code Highlighter .

An auxiliary function that returns an array of approach half-degrees for all vertices of the network.

int ?[] GetInputNodesArray()
{
int ?[] array = new int ?[ this .nodes.Count];
for ( int i = 0; i < this .nodes.Count; i++)
{
array[i] = this .nodes[i].LinkedDownNodes.Count;
}
return array;
}

* This source code was highlighted with Source Code Highlighter .

And finally, the algorithm:

public void TopologicSort()
{
List < List <GraphNode>> levels = new List < List <GraphNode>>();
int ?[] workArray = GetInputNodesArray();

int completedCounter = 0;
int currentLevel = 0;

bool pathFound;
while (completedCounter != this .nodes.Count)
{
levels.Add( new List <GraphNode>());

// ,
// , ,
// .
for ( int i = 0; i < this .nodes.Count; i++)
{
if (workArray[i] == 0)
{
workArray[i] = null ;
}
}

for ( int i = 0; i < this .nodes.Count; i++)
{
if (workArray[i] == null )
{
// ,
//
//
levels[currentLevel].Add( this .nodes[i]);
this .nodes[i].Tag = currentLevel; //

foreach (GraphNode node in this .nodes[i].LinkedNodes)
{
int linkedNode = this .nodes.IndexOf(node);
workArray[linkedNode]--;
}

workArray[i] = -1; //

completedCounter++;
}
}

currentLevel++;
}
}

* This source code was highlighted with Source Code Highlighter .

Epilogue

Compilers do not limit the use of this algorithm; it can also be used, for example, when programming neural networks, or planning large projects.
Next time there will be a story about the shortest path search algorithms on a graph (Dijkstra's algorithm and Wave Front algorithm).

Sources

Program and Sources in C #: Download
This link is much more functional program and a few examples of networks for sorting.
Presentation with omitted steps of the algorithm: Download