Algorithms on graphs - Part 1: Search in depth and the problem of deadlocks
Recently on Habré there was an article devoted to algorithms on graphs. With the permission of the author, my first habratopic will continue the cycle.
I would like to highlight the issues of using some algorithms for solving programming problems.
Quite a vital example that not one developer has encountered is deadlock . In essence, deadlock is a deadlock, as a result of which the system, or some separate processes, begin to compete for one resource.
In life, such situations occur, for example, when two people want to miss each other at the entrance, suppose, to the audience. However, after 3-4 phrases “only after you!”, Someone will pass first.
At the software level, it is becoming more and more difficult until programs are able to think that the computer equivalent of the phrase “only after you!” Will repeat until the reboot.
How can the execution system affect this process? This is where algorithms on graphs come to our rescue.
To begin with, we will define what will be the elements of our graph, and how to compose it.
Take a more “machine-based” example: a single-threaded java application with Internet access. Imagine that our code and message output system will be executed in one thread, in this case, before opening the connection, a request is initiated by the user whether he really trusts this application to use the Internet. A block occurs, the code will not complete until the user clicks OK, but the message will be displayed only after the code is completed. Let's try to build a graph for this example.

')
The vertices denote the functional units of the program, arcs - external requests necessary to continue the work node.
We define the contour as the path from any vertex to itself. In this case, on our graph each contour will illustrate the deadlock that has arisen.
Now everything is ready for the formal description of the algorithm itself.
1. Number all vertices of the graph
2. Mark all vertices of the graph as new
3. Mark all arcs of the graph as new
4. Put an arbitrary vertex of the graph on the stack
5. While the stack is not empty, read (without pushing) the last vertex from the stack and apply the Find (Node V) procedure to it.
6. If the stack is empty, but new peaks remain, put any of the new ones in the stack and go to step 5
Procedure Find (Node V)
For vertex V, remove the sign of novelty;
For all new arcs D, from the adjacency list of V
Remove from D a sign of novelty;
If arc D leads to a new vertex
Push D.LinkNode to the stack;
Run Find (Node D.LinkNode);
End (If);
If the top is not new and is on the stack
Read the stack from the current vertex to D.LinkNode and put the data into the storage of detected contours
End (If);
End (for all new arcs D);
Push V out of the stack;
End (Find procedure);
Where D.LinkNode is the vertex pointed to by the arc.
An example implementation of the algorithm:
First we need to declare the data type for the graph and its vertices
Now we are implementing a class that searches for contours.
And, actually, our main functions:
The stack was intentionally implemented by the list, since we will need to read the contours found from it without pushing the elements
Graphically, the algorithm can be considered as follows:
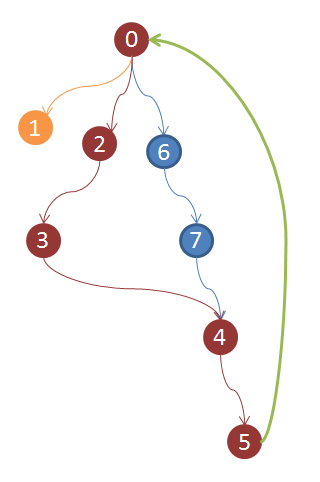
From vertex “0”, which is the beginning of the path, we move downward, if at the next step the algorithm finds an arc pointing to a vertex in the stack (in this case, the arc starts from vertex “4”), a contour is formed from the vertices of the stack ( example: 0-2-3-4-5-0), respectively, if the arc points to a no longer new vertex, but already pushed out of the stack (for example, to the vertex “1”), a contour does not occur.
This algorithm is known as a depth search in a directed graph.
Thus, the runtime can only track all method calls and, periodically, check for locks.
How to deal with blockages found? Sometimes deadlock is so confusing that it is much easier to restart interlocked code, in any case, this should be decided individually for a particular system.
The next time (for my part) is the topological sorting algorithm, which, among other things, can be applied when compiling and analyzing the chain of neuron activations in a neural network.
UPD : Added sample code
UPD2 : Transferred to algorithms, thanks
I would like to highlight the issues of using some algorithms for solving programming problems.
Quite a vital example that not one developer has encountered is deadlock . In essence, deadlock is a deadlock, as a result of which the system, or some separate processes, begin to compete for one resource.
In life, such situations occur, for example, when two people want to miss each other at the entrance, suppose, to the audience. However, after 3-4 phrases “only after you!”, Someone will pass first.
At the software level, it is becoming more and more difficult until programs are able to think that the computer equivalent of the phrase “only after you!” Will repeat until the reboot.
How can the execution system affect this process? This is where algorithms on graphs come to our rescue.
To begin with, we will define what will be the elements of our graph, and how to compose it.
Take a more “machine-based” example: a single-threaded java application with Internet access. Imagine that our code and message output system will be executed in one thread, in this case, before opening the connection, a request is initiated by the user whether he really trusts this application to use the Internet. A block occurs, the code will not complete until the user clicks OK, but the message will be displayed only after the code is completed. Let's try to build a graph for this example.

')
The vertices denote the functional units of the program, arcs - external requests necessary to continue the work node.
We define the contour as the path from any vertex to itself. In this case, on our graph each contour will illustrate the deadlock that has arisen.
Now everything is ready for the formal description of the algorithm itself.
1. Number all vertices of the graph
2. Mark all vertices of the graph as new
3. Mark all arcs of the graph as new
4. Put an arbitrary vertex of the graph on the stack
5. While the stack is not empty, read (without pushing) the last vertex from the stack and apply the Find (Node V) procedure to it.
6. If the stack is empty, but new peaks remain, put any of the new ones in the stack and go to step 5
Procedure Find (Node V)
For vertex V, remove the sign of novelty;
For all new arcs D, from the adjacency list of V
Remove from D a sign of novelty;
If arc D leads to a new vertex
Push D.LinkNode to the stack;
Run Find (Node D.LinkNode);
End (If);
If the top is not new and is on the stack
Read the stack from the current vertex to D.LinkNode and put the data into the storage of detected contours
End (If);
End (for all new arcs D);
Push V out of the stack;
End (Find procedure);
Where D.LinkNode is the vertex pointed to by the arc.
An example implementation of the algorithm:
First we need to declare the data type for the graph and its vertices
public class GraphNode
{
public bool New;
public List <GraphNode> Links;
}
* This source code was highlighted with Source Code Highlighter .public class Graph
{
public List <GraphNode> Nodes;
}
* This source code was highlighted with Source Code Highlighter .Now we are implementing a class that searches for contours.
public static class PathFinder
{
static List <GraphNode> list;
static List < List <GraphNode>> paths;
public static List < List <GraphNode>> Find(Graph graph)
static void InternalFind(GraphNode node)
}
* This source code was highlighted with Source Code Highlighter .And, actually, our main functions:
static List < List <GraphNode>> Find(Graph graph)
{
list = new List <GraphNode>(); //
paths = new List < List <GraphNode>>(); //
foreach (GraphNode node in graph.Nodes)
{
node.New = true ;
}
list.Add(graph.Nodes[0]); //
bool done = false ;
while (!done)
{
while (list.Count > 0)
{
InternalFind(list[list.Count - 1]);
}
//
done = true ;
foreach (GraphNode node in graph.Nodes)
{
if (node.New)
{
list.Add(node);
done = false ;
break ;
}
}
}
return paths;
}
* This source code was highlighted with Source Code Highlighter .The stack was intentionally implemented by the list, since we will need to read the contours found from it without pushing the elements
static void InternalFind(GraphNode node)
{
node.New = false ;
foreach (GraphNode nextNode in node.Links) //
{
if (nextNode.New)
{
list.Add(nextNode);
InternalFind(nextNode);
}
else if (list.IndexOf(nextNode) != -1) // ,
{
List <GraphNode> newPath= new List <GraphNode>();
int firstElement = list.IndexOf(nextNode);
for ( int i = firstElement; i < list.Count; i++)
{
newPath.Add(list[i]);
}
paths.Add(newPath);
}
}
list.Remove(node);
}
* This source code was highlighted with Source Code Highlighter .Graphically, the algorithm can be considered as follows:

From vertex “0”, which is the beginning of the path, we move downward, if at the next step the algorithm finds an arc pointing to a vertex in the stack (in this case, the arc starts from vertex “4”), a contour is formed from the vertices of the stack ( example: 0-2-3-4-5-0), respectively, if the arc points to a no longer new vertex, but already pushed out of the stack (for example, to the vertex “1”), a contour does not occur.
This algorithm is known as a depth search in a directed graph.
Thus, the runtime can only track all method calls and, periodically, check for locks.
How to deal with blockages found? Sometimes deadlock is so confusing that it is much easier to restart interlocked code, in any case, this should be decided individually for a particular system.
The next time (for my part) is the topological sorting algorithm, which, among other things, can be applied when compiling and analyzing the chain of neuron activations in a neural network.
UPD : Added sample code
UPD2 : Transferred to algorithms, thanks
Source: https://habr.com/ru/post/66586/
All Articles