Let's play in life
Imagine a piece of paper in a cage. I suspect that already at this stage, some habraedy guessed what was going to be discussed. Well, my respect to them. The rest continue to imagine a piece of paper in the cell. In all details. In the smallest detail.
Now imagine that on this simple piece of paper we will create a simple, but therefore equally impressive life simulator. No more, no less. Of course, it will be very simplified, but in order to understand something difficult, you must start with a simple one, right? This simulator can be applied to a variety of sciences and with each of them it will have many interesting points of contact. From sociology to astronomy, from biology to electrical engineering.
Okay, enough zavlekalok. It's time to hit the math.
')

Once upon a time, in the 1940s, the notorious John von Neumann set out to design a machine that can reproduce itself. Oddly enough, but he succeeded. True, the rules of this car were so complex that it was not widely used.
After 30 years, another scientist named John Conway (yes, John is a very popular name) became interested in this machine and decided to simplify it. It is strange again, but he succeeded. Talented scientists, to be sure.
So. Again we quickly draw a paper with cells in my head. The rules are very simple:
A simple example of the evolution of five variants of triplets (figures of three cells):

Nothing complicated, is it? By and large, only the initial arrangement of living cells depends on the player, after which they will live on their own, and the creator will only follow them. But then there is the very reason why this game has been interested in for almost 40 years.
Just imagine the number of cell placement options in a minimal field, even if at least 10 * 10 cells. This is 2 100 . And each of these options will evolve. Some - only a few dozen moves, and some can get stuck. What can we say then about large fields of type 100 * 100 or even more so about those closed according to the torus principle.
During field trials of this game, first on paper, and then using computer simulation, many figures were identified, which can be sorted out according to their behavior into several classes.
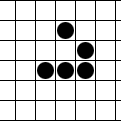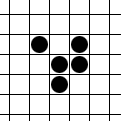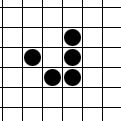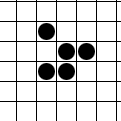
The simplest example of a moving figure is the glider (glider):
Not interested?
Then take a look at the gun:
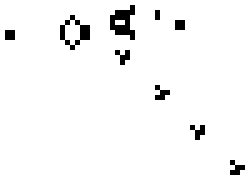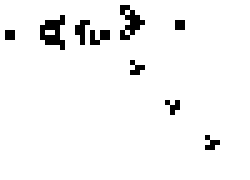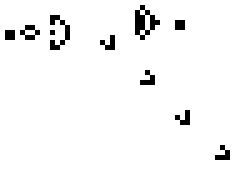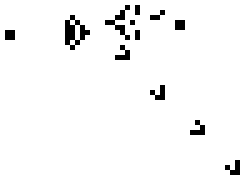
In this form, with a small distance, when the boundaries between the cells are smeared, this animation already resembles something biological, doesn’t it? By the way, the gun "shoots" those same gliders.
Before I give you the opportunity to try to make figures yourself, let me say a few words about the benefits of all this stuff for science.
Generally speaking, in scientific terms, this game is a discrete dynamic system whose behavior is completely defined in terms of local dependencies , and in short, a cellular automaton. That is, the lattice, in which each cell has a finite number of states, and this state itself is determined through rigidly defined transition rules.
This game is almost the simplest cellular automaton. And imagine that each cell has not two, but about a dozen different states, and their changes depend not only on the neighboring 8 cells, but also on 16 on the “second perimeter”.
Such cellular automata are one of the simplest examples of what are sometimes called "self-organized systems." This subject area attracted the attention of scientists and mathematicians from various fields. It studies the construction of complex structures and behaviors based on very simple rules. For example, the appearance of rose petals or stripes on a zebra from growing near cells. Therefore, the study of finite automata can lead to completely unexpected results in completely different sciences. For example, the evolution of some complex colonies miraculously schematically repeat the stages of development of spiral galaxies. As well as they largely coincide with the laws of the behavior of populations of primitive organisms.
Well, now it is time to try it yourself.
Forward to the test. And yes be with you random))
Now imagine that on this simple piece of paper we will create a simple, but therefore equally impressive life simulator. No more, no less. Of course, it will be very simplified, but in order to understand something difficult, you must start with a simple one, right? This simulator can be applied to a variety of sciences and with each of them it will have many interesting points of contact. From sociology to astronomy, from biology to electrical engineering.
Okay, enough zavlekalok. It's time to hit the math.
')

Once upon a time, in the 1940s, the notorious John von Neumann set out to design a machine that can reproduce itself. Oddly enough, but he succeeded. True, the rules of this car were so complex that it was not widely used.
After 30 years, another scientist named John Conway (yes, John is a very popular name) became interested in this machine and decided to simplify it. It is strange again, but he succeeded. Talented scientists, to be sure.
rules
So. Again we quickly draw a paper with cells in my head. The rules are very simple:
- Each cell can be in one of two states: live (filled) or dead (empty).
- Each turn of each cell is determined by its state and the state of all its 8 neighbors.
- If it is an empty cell and there are exactly 3 neighbors, then this cell comes to life. In all other cases, the empty cell remains empty.
- If it is a living cell, then the number of living neighbors is calculated.
- If the neighbors are 0 or 1, then the cell dies of loneliness.
- If there are 2 or 3 neighbors, then the cell continues to live.
- If there are 4 neighbors or more, then the cell dies from overcrowding.
A simple example of the evolution of five variants of triplets (figures of three cells):

Nothing complicated, is it? By and large, only the initial arrangement of living cells depends on the player, after which they will live on their own, and the creator will only follow them. But then there is the very reason why this game has been interested in for almost 40 years.
Just imagine the number of cell placement options in a minimal field, even if at least 10 * 10 cells. This is 2 100 . And each of these options will evolve. Some - only a few dozen moves, and some can get stuck. What can we say then about large fields of type 100 * 100 or even more so about those closed according to the torus principle.

Figures
During field trials of this game, first on paper, and then using computer simulation, many figures were identified, which can be sorted out according to their behavior into several classes.
- Stable figures: figures that remain unchanged
- Periodic figures: figures whose state is repeated after a certain number of generations
- Moving figures: figures in which the state is repeated, but with some displacement
- Guns: figures in which the state is repeated, but additionally, there is a moving figure
- Locomotives: moving figures that leave traces in the form of stable or periodic figures
- Devourers: steady figures that can survive collisions with some moving figures
The simplest example of a moving figure is the glider (glider):

Not interested?
Then take a look at the gun:
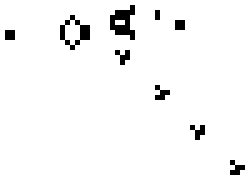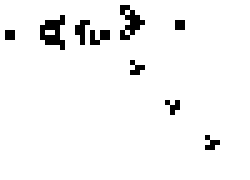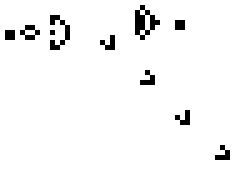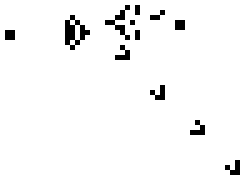
In this form, with a small distance, when the boundaries between the cells are smeared, this animation already resembles something biological, doesn’t it? By the way, the gun "shoots" those same gliders.
Interest for science
Before I give you the opportunity to try to make figures yourself, let me say a few words about the benefits of all this stuff for science.
Generally speaking, in scientific terms, this game is a discrete dynamic system whose behavior is completely defined in terms of local dependencies , and in short, a cellular automaton. That is, the lattice, in which each cell has a finite number of states, and this state itself is determined through rigidly defined transition rules.
This game is almost the simplest cellular automaton. And imagine that each cell has not two, but about a dozen different states, and their changes depend not only on the neighboring 8 cells, but also on 16 on the “second perimeter”.
Such cellular automata are one of the simplest examples of what are sometimes called "self-organized systems." This subject area attracted the attention of scientists and mathematicians from various fields. It studies the construction of complex structures and behaviors based on very simple rules. For example, the appearance of rose petals or stripes on a zebra from growing near cells. Therefore, the study of finite automata can lead to completely unexpected results in completely different sciences. For example, the evolution of some complex colonies miraculously schematically repeat the stages of development of spiral galaxies. As well as they largely coincide with the laws of the behavior of populations of primitive organisms.
Practice
Well, now it is time to try it yourself.
- Here you can and should read about "life" in more detail. It describes the many shapes and principles. And indeed a lot of useful things.
- Here you can play "life" on the flash. There are no settings. Everything is simplified to a minimum. Pure for your reference.
- Here you can download the program emulator with advanced features. Adjust the speed of time. Ability to save and load initial configurations. Resizable field. In general, complete freedom of action. For hardcore. Unfortunately, only under Windows.
- Well, here lies a similar emulator for all platforms (Windows (2000+), Mac OS X (10.3.9+) and Linux (GTK +)). I did not launch it myself, but judging by the description, it has no less possibilities than the previous program.
Forward to the test. And yes be with you random))
Source: https://habr.com/ru/post/63848/
All Articles