Mini-report on participation in ICFPC 2009
ICFPC is an annual competition of programmers. Here is my participation report.
The task is described a hundred times, you can see here habrahabr.ru/blogs/icfpc/63279
In a nutshell:
Several satellites revolve around the earth, we control one of them. We must complete the job by writing a series of engine starts. Tasks were checked on a virtual simulator machine, programs for which were provided by the organizers.
')
Because I did not know in advance whether I would have time to participate, I found myself without a team, this seriously affected the decision-making process. It was clear that it was very difficult for one to win, so I decided not to chase after the points, but to make a “beautiful” decision even if it would be clear that I don’t have time. Also along the way, I was periodically distracted by interesting, but not very important things for getting points, which I will write about.
I will remind the list of tasks (in each of 4 scenarios)
Friday 26, Evening. Leaving work, I glanced over the shoulder of a colleague reading the assignment, and managed to catch only a couple of keywords “virtual machine” and “satellite”. On the way home on the train, I wondered what the task might be and decided that most likely I would have to write a compiler into the language of some VM. When I got home and finally read the assignment, I realized that writing the compiler was canceled - the VM was just trivial. It was possible to write a compiler, but in the opposite direction - from the VM language to the machine code.
The language was chosen Python. For visualization, I planned to use Mathematica. Because a working laptop with licensed Mathematics was forgotten at work, it was urgently downloaded from torrents and installed.
I decided not to fool at first and dashed off the Orbital Machine on Python in less than an hour. After that, I spent an hour searching for the elusive bug that was found in the end ... in the text of the assignment. By that time, the organizers posted a new version of the specification, in which the comparison parameter was defined differently. After fixing the "bug" everything worked and later never buggy. In the meantime, debugging the VM, I pulled the values of physical constants from the organizers code (they differed from the specifications in a pair of bits). So Friday night went by and I went to bed.
Saturday:
The task was clearly divided into two parts. Firstly, we have the physics of satellite motion, which would not be bad to implement. Secondly, the VM works with finite precision, so even exact solutions need to be customized, plus in the fourth task, the need for global optimization of the SCORE (Fuel, Time) function is clearly seen, which can only be done numerically. Thinking I decided that there are three strategies that I cite in order of increasing complexity:
1. Purely numerical brute force method
2. Purely analytical option
3. Combined
Method number 1, no physics: Just simulate the trajectory with some initial parameters taken from the ceiling, which we improve using numerical optimization methods (gradient descent, Monte Carlo, etc.). You need a very fast VM and a bit of heuristics. Ideal for singles who want to get "maximum points at any cost." He 100% solves the first three tasks, but in the fourth he will be already strained, because the parameter space for optimization is huge and the algorithms will converge very slowly.
Method number 2, only physics + some heuristics: All the problems in the form in which they were formulated in the first version of the condition are solved exactly (then they added the Moon to the fourth problem, which made things a bit more complicated). Therefore, you can sit down at the formula and make a "smart" decision. The disadvantage is that, as I wrote above, the exact solutions do not fit; they need to be corrected.
Method number 3 takes the best from the first two. We use exact solutions (which are corrected numerically). Having a good initial approximation will significantly accelerate global time-to-fuel optimization. The disadvantage is too much work for one person.
I decided to start from Point 2 and, if possible, move towards the optimal solution 3.
First of all, it was logical to implement the so-called one described in Wikipedia. Goman's transition. The bottom line is that we make two control impulses: the first translates into an intermediate orbit, the second to the final one.
In the picture: the moment of transition to the target orbit, the place where the engines were turned on is bold.
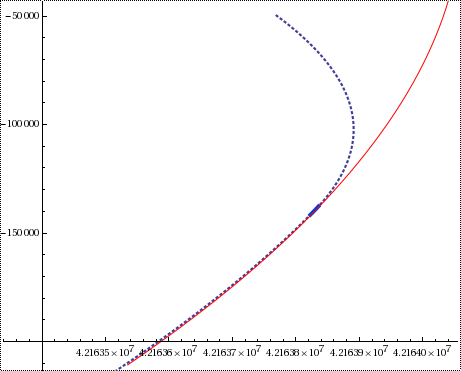
The task was solved with an eye to the future, and I immediately wrote a fairly advanced class Orbit, which subsequently expanded many times. It is interesting that many people found the book Orbital Mechanics and considered trajectories by three points. But in our task, besides the position, the speed is also known, therefore we can count the trajectories by TWO points. In addition to the standard parameters of the orbit, a bunch of useful things were immediately considered: semi-axes, eccentricity, energy, angular momentum, orbital period.
Looking ahead, I’ll say that the intelligent integrator never got around to writing. All calculations were based on the last two points of the VM simulation and the third (next) predicted magic function getNextXY (you can say that it is an integrator-predictor embryo, if you run it in a cycle, you get a full-fledged predictor, but slow))))
As the coordinates I chose, polar with the Earth in the center. In these coordinates, all possible free orbits are described by one equation with three parameters:
where a is the semi-major axis, e is the eccentricity, delta is the angle of rotation of the orbit.
Along the way, I derived formulas for tangents to an ellipse at an arbitrary point and a formula for ellipses touching each other at a given point (in fact, there are infinitely many such ellipses). For the third task, I wanted to derive a formula that finds a third tangent to them in two given orbits. But the end of the Lightning Round was coming and I decided to add at least something, but I did not have time to write the serialization of the solution to a file.

It is interesting that in the first problem in all scenarios, exact solutions were earned without a file. It was quite impressive: two simulation steps were taken, the trajectories and impulses of the engine were calculated, which were then simply performed to the end without any feedback.
After the end of the Lightning Round, the organizers posted a new version of the task, which added difficulties in the form of the moon in the fourth task. This excluded her from the class of exactly solvable. But since The moon is lighter than Earth, it is possible to calculate approximate trajectories that will be fairly accurate several turns and take them as the initial for optimization. In fact, this is the same ellipse, the axis of which slowly changes with time (much shorter than the orbital period).
By Saturday evening, everything worked and solved the first 4 scenarios “at two points”, the solutions were checked and uploaded to the server. At the end, I derived a formula for finding the points of intersection of elliptical orbits, in the morning to add flights along non-touching paths and go to sleep.

On Sunday morning, rereading the next revision of the condition, I was interested in the fact that in the first task it turns out to give more points if you burn the maximum fuel. This proved fatal to further progress.
First, I wrote the simplest algorithm for “burning” the fuel, counting how much is needed for the transition, then spend the excess, pulling the pull back and forth with small impulses and correcting the orbit if it deviates by more than 0.1%. This gave almost one and a half times more points than on Saturday.
And then I thought “what is the best way? probably a hyperbolic orbit! ” And I was stuck (and there was no one to expose). All Sunday I spent on the synthesis of my almost finished code. I wanted to add hyperbolas and parabolas to the working ellipses (which later were broken more than once during the course of the case). And by Sunday evening, my code was already solving the first task “in the optimal way, using two points”, flying right from the third time step to the desired orbit and braking there.

The most difficult was not the calculation of the intersection point of two orbits (both arbitrary curves of the second order), but the prediction of flight time. Time is proportional to the area of the sector, it was not possible to find a ready-made formula for an elliptical / hyperbolic sector on the Internet and it was necessary to derive it. When I saw this horror (which Mathematics helpfully spit out to me) - a hyperbolic arctangent from a complex argument, I almost fell off my chair. But in the end, we managed to unravel and we got the usual arctangent for the ellipse and the logarithm for the hyperbola (from generous fractions, well and good)). It is worth noting that it was almost a waste of time (albeit entertaining). Flight time was needed to know when we cross the target orbit, but you can just stupidly check every step of the simulation (even with an analytical answer, I had to “fly the last meters” step by step, because the error in hyperbolic orbits is big because of the high speed )
Along the way, I messed up the signs, but everything worked. But when I did draw a trajectory, I almost burst out laughing. The satellite flew to the desired trajectory and there abruptly turned and flew in the opposite direction. The green line is the calculated trajectory, the red line is like flying.
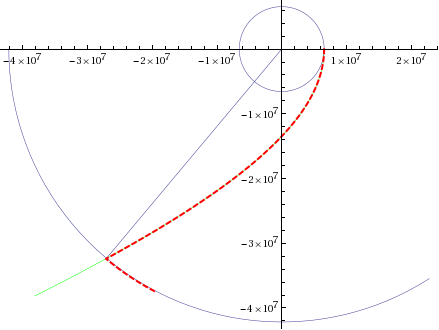
The rest of Sunday evening I spent catching mistakes in signs, because All formulas depended strongly on the relative position of the orbits and the signs of the coordinates.
The next day (having slept for three hours), already at work, I slightly cleaned up the code of what worked and quickly solved the second task. But for some reason, despite the fact that my satellite followed the target with an accuracy of better than 900 meters, no points were given. I added automatic stabilization of the orbit and achieved accuracy of a few centimeters for tens of thousands of seconds, but I did not give points. Having been in a stupor for about 15 minutes, I almost had a tantrum. I realized that I was flying for the "ghost", but rather for the reflection of the goal. Because the organizers were too lazy to draw a picture in the task, I got it wrong in the signs and the target vector was the opposite! Adding minuses to reading parameters immediately solved all the problems.
Considering that I had few points, I managed at the last moment to fill in one non-working solution and lose about 100 more. As a result, there are about 1000.
Findings:
Pros:
- got a lot of fun (and that was the goal)
- wrote a bunch of formulas and even partially applied them
in a team where everyone concentrates on one subtask, these formulas would be of great benefit.
Minuses:
- without the support of numerical methods, the formulas were of little use (well, it was clear from the beginning)
- because there was no “pressure of responsibility” often distracted by nonsense
- The organizers might be more concerned with the compatibility of different architectures, perhaps the option would be to use only integer arithmetic in the VM (although I did not encounter these problems). Well, the bugs in the tasks are not pleased.
The task is described a hundred times, you can see here habrahabr.ru/blogs/icfpc/63279
In a nutshell:
Several satellites revolve around the earth, we control one of them. We must complete the job by writing a series of engine starts. Tasks were checked on a virtual simulator machine, programs for which were provided by the organizers.
')
Because I did not know in advance whether I would have time to participate, I found myself without a team, this seriously affected the decision-making process. It was clear that it was very difficult for one to win, so I decided not to chase after the points, but to make a “beautiful” decision even if it would be clear that I don’t have time. Also along the way, I was periodically distracted by interesting, but not very important things for getting points, which I will write about.
I will remind the list of tasks (in each of 4 scenarios)
- Jump from one circular orbit to another circular
- Also, only in the second orbit there is another satellite and we need to approach it and follow it.
- Also, the orbits of both satellites are arbitrary ellipses.
- 10 satellites + gas station. We must visit them all (fly by).
Friday 26, Evening. Leaving work, I glanced over the shoulder of a colleague reading the assignment, and managed to catch only a couple of keywords “virtual machine” and “satellite”. On the way home on the train, I wondered what the task might be and decided that most likely I would have to write a compiler into the language of some VM. When I got home and finally read the assignment, I realized that writing the compiler was canceled - the VM was just trivial. It was possible to write a compiler, but in the opposite direction - from the VM language to the machine code.
The language was chosen Python. For visualization, I planned to use Mathematica. Because a working laptop with licensed Mathematics was forgotten at work, it was urgently downloaded from torrents and installed.
I decided not to fool at first and dashed off the Orbital Machine on Python in less than an hour. After that, I spent an hour searching for the elusive bug that was found in the end ... in the text of the assignment. By that time, the organizers posted a new version of the specification, in which the comparison parameter was defined differently. After fixing the "bug" everything worked and later never buggy. In the meantime, debugging the VM, I pulled the values of physical constants from the organizers code (they differed from the specifications in a pair of bits). So Friday night went by and I went to bed.
Saturday:
The task was clearly divided into two parts. Firstly, we have the physics of satellite motion, which would not be bad to implement. Secondly, the VM works with finite precision, so even exact solutions need to be customized, plus in the fourth task, the need for global optimization of the SCORE (Fuel, Time) function is clearly seen, which can only be done numerically. Thinking I decided that there are three strategies that I cite in order of increasing complexity:
1. Purely numerical brute force method
2. Purely analytical option
3. Combined
Method number 1, no physics: Just simulate the trajectory with some initial parameters taken from the ceiling, which we improve using numerical optimization methods (gradient descent, Monte Carlo, etc.). You need a very fast VM and a bit of heuristics. Ideal for singles who want to get "maximum points at any cost." He 100% solves the first three tasks, but in the fourth he will be already strained, because the parameter space for optimization is huge and the algorithms will converge very slowly.
Method number 2, only physics + some heuristics: All the problems in the form in which they were formulated in the first version of the condition are solved exactly (then they added the Moon to the fourth problem, which made things a bit more complicated). Therefore, you can sit down at the formula and make a "smart" decision. The disadvantage is that, as I wrote above, the exact solutions do not fit; they need to be corrected.
Method number 3 takes the best from the first two. We use exact solutions (which are corrected numerically). Having a good initial approximation will significantly accelerate global time-to-fuel optimization. The disadvantage is too much work for one person.
I decided to start from Point 2 and, if possible, move towards the optimal solution 3.
First of all, it was logical to implement the so-called one described in Wikipedia. Goman's transition. The bottom line is that we make two control impulses: the first translates into an intermediate orbit, the second to the final one.
In the picture: the moment of transition to the target orbit, the place where the engines were turned on is bold.

The task was solved with an eye to the future, and I immediately wrote a fairly advanced class Orbit, which subsequently expanded many times. It is interesting that many people found the book Orbital Mechanics and considered trajectories by three points. But in our task, besides the position, the speed is also known, therefore we can count the trajectories by TWO points. In addition to the standard parameters of the orbit, a bunch of useful things were immediately considered: semi-axes, eccentricity, energy, angular momentum, orbital period.
Looking ahead, I’ll say that the intelligent integrator never got around to writing. All calculations were based on the last two points of the VM simulation and the third (next) predicted magic function getNextXY (you can say that it is an integrator-predictor embryo, if you run it in a cycle, you get a full-fledged predictor, but slow))))
As the coordinates I chose, polar with the Earth in the center. In these coordinates, all possible free orbits are described by one equation with three parameters:
R(PHI)=a*(1-e^2)/(1+e*cos(delta+PHI)) ,where a is the semi-major axis, e is the eccentricity, delta is the angle of rotation of the orbit.
Along the way, I derived formulas for tangents to an ellipse at an arbitrary point and a formula for ellipses touching each other at a given point (in fact, there are infinitely many such ellipses). For the third task, I wanted to derive a formula that finds a third tangent to them in two given orbits. But the end of the Lightning Round was coming and I decided to add at least something, but I did not have time to write the serialization of the solution to a file.

It is interesting that in the first problem in all scenarios, exact solutions were earned without a file. It was quite impressive: two simulation steps were taken, the trajectories and impulses of the engine were calculated, which were then simply performed to the end without any feedback.
After the end of the Lightning Round, the organizers posted a new version of the task, which added difficulties in the form of the moon in the fourth task. This excluded her from the class of exactly solvable. But since The moon is lighter than Earth, it is possible to calculate approximate trajectories that will be fairly accurate several turns and take them as the initial for optimization. In fact, this is the same ellipse, the axis of which slowly changes with time (much shorter than the orbital period).
By Saturday evening, everything worked and solved the first 4 scenarios “at two points”, the solutions were checked and uploaded to the server. At the end, I derived a formula for finding the points of intersection of elliptical orbits, in the morning to add flights along non-touching paths and go to sleep.

On Sunday morning, rereading the next revision of the condition, I was interested in the fact that in the first task it turns out to give more points if you burn the maximum fuel. This proved fatal to further progress.
First, I wrote the simplest algorithm for “burning” the fuel, counting how much is needed for the transition, then spend the excess, pulling the pull back and forth with small impulses and correcting the orbit if it deviates by more than 0.1%. This gave almost one and a half times more points than on Saturday.
And then I thought “what is the best way? probably a hyperbolic orbit! ” And I was stuck (and there was no one to expose). All Sunday I spent on the synthesis of my almost finished code. I wanted to add hyperbolas and parabolas to the working ellipses (which later were broken more than once during the course of the case). And by Sunday evening, my code was already solving the first task “in the optimal way, using two points”, flying right from the third time step to the desired orbit and braking there.

The most difficult was not the calculation of the intersection point of two orbits (both arbitrary curves of the second order), but the prediction of flight time. Time is proportional to the area of the sector, it was not possible to find a ready-made formula for an elliptical / hyperbolic sector on the Internet and it was necessary to derive it. When I saw this horror (which Mathematics helpfully spit out to me) - a hyperbolic arctangent from a complex argument, I almost fell off my chair. But in the end, we managed to unravel and we got the usual arctangent for the ellipse and the logarithm for the hyperbola (from generous fractions, well and good)). It is worth noting that it was almost a waste of time (albeit entertaining). Flight time was needed to know when we cross the target orbit, but you can just stupidly check every step of the simulation (even with an analytical answer, I had to “fly the last meters” step by step, because the error in hyperbolic orbits is big because of the high speed )
Along the way, I messed up the signs, but everything worked. But when I did draw a trajectory, I almost burst out laughing. The satellite flew to the desired trajectory and there abruptly turned and flew in the opposite direction. The green line is the calculated trajectory, the red line is like flying.

The rest of Sunday evening I spent catching mistakes in signs, because All formulas depended strongly on the relative position of the orbits and the signs of the coordinates.
The next day (having slept for three hours), already at work, I slightly cleaned up the code of what worked and quickly solved the second task. But for some reason, despite the fact that my satellite followed the target with an accuracy of better than 900 meters, no points were given. I added automatic stabilization of the orbit and achieved accuracy of a few centimeters for tens of thousands of seconds, but I did not give points. Having been in a stupor for about 15 minutes, I almost had a tantrum. I realized that I was flying for the "ghost", but rather for the reflection of the goal. Because the organizers were too lazy to draw a picture in the task, I got it wrong in the signs and the target vector was the opposite! Adding minuses to reading parameters immediately solved all the problems.
Considering that I had few points, I managed at the last moment to fill in one non-working solution and lose about 100 more. As a result, there are about 1000.
Findings:
Pros:
- got a lot of fun (and that was the goal)
- wrote a bunch of formulas and even partially applied them
in a team where everyone concentrates on one subtask, these formulas would be of great benefit.
Minuses:
- without the support of numerical methods, the formulas were of little use (well, it was clear from the beginning)
- because there was no “pressure of responsibility” often distracted by nonsense
- The organizers might be more concerned with the compatibility of different architectures, perhaps the option would be to use only integer arithmetic in the VM (although I did not encounter these problems). Well, the bugs in the tasks are not pleased.
Source: https://habr.com/ru/post/63354/
All Articles