Recommendation Systems: Artificial Immune Systems and the Effect of Idiotypes
Recommendation Systems:
- Car Tips
- Cold start
- Introduction to hybrid systems
- Artificial immune systems and the effect of idiotypes
Reading various publications about data mining and recommendation systems, I accidentally stumbled upon one of the most interesting approaches to the implementation of such systems. It is based on the concept of an artificial immune system (IIS, Artificial immune system ), according to which some properties of the immune system of living organisms, including the ability to learn and memorize, are implemented in a computer system. A recommendation system uses a model that describes the concentration of antibodies that respond to a particular antigen. Of particular interest is the so-called effect idiotypes ( Idiotype ), showing that the concentration of antibodies depends not only on their similarity to the antigen, but also on the similarities with each other.
For those who are not familiar with biology, I will briefly explain the essence of the matter. An antigen is a substance that, when ingested, causes an immune system to respond. In response, it produces antibodies , a certain class of proteins that are used to identify and neutralize stimuli. In our case, the antigen is the user, and the antibodies are the objects with which you compare it. To make it easier to imagine, I suggest that we consider a collective filtering system, where other users are antibodies.
Now let's get down to business. An equation describing the concentration of antibodies proposed J. Doyne Farmer :
')

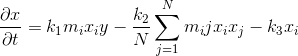
Where:
m i - the similarity between the antigen and antibody i,
x i and x j - the concentration of antibodies i and j, respectively,
y is the concentration of antigen,
m ij - the similarity between antibodies i and j,
k 1 - coefficient of stimulation
k 2 - the coefficient of suppression,
k 3 - the mortality rate
N is the number of antibodies.
Consider each addend separately:
The algorithm of such a system is quite simple.
1. We take from the database the first antibody and calculate its concentration according to the described formula.
2. The result, obviously, can be both positive and negative, if it is below a certain minimum - discard the antibody and take the following.
3. We continue this cycle until the antibodies run out or the system does not stabilize , that is, if the result is almost unchanged over the last plus or minus ten iterations.
IIS has two main differences from other systems of recommendations:
At the request of readers, I will give a simple example of using IIS. Suppose we have a correlation table of users A, B, C and Y obtained by some method. Our system works on the principle of collective filtering, so we need to find two users similar to user Y, and use their voices to further predict the voice of user Y In this example, I will not consider how we got this table and how we use the result in the future. Consider only how the effect of idiotypes will affect the choice of the users we need.
For an ordinary system, users B and C will be the obvious choice, and they will be right too.
Let's see what IIS offers. Calculate the concentration for users B and C. Let the formula be in front of your eyes:
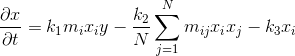
Take k 1 = 0.3, k 2 = 0.2, k 3 = 0.1, y = 1, since we need to select two users, N = 2. Then:
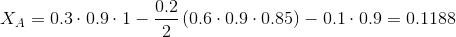
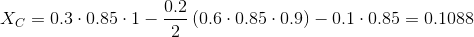
Let us assume that the minimum value of concentration accepted by us is 0.11. X C clearly does not fit into him, so we need to look for a replacement for him. Consider user B:
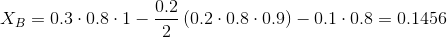
As you can see, despite the fact that its similarity with user Y is slightly less than user C, its concentration is noticeably greater, since B is less similar to A than C. So, as we replaced user C with B, we must recalculate and User A's concentration, because it depends on other users:

By calculating the concentration, we can accordingly adjust the similarity of users with user Y:
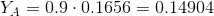
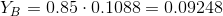

According to the published test results, the IIS actually give more accurate results than other systems, but the reason for their success is not in the influence of any particular factor from those considered above, but in their interaction. For details, I advise you to look into the sources:
1. Steve Cayzer and Uwe Aickelin " A Recommender System Based on the Immune Network " (pdf)
2. Steve Cayzer and Uwe Aickelin " On the Effects of Idiotypic Interactions for Recommendation
Communities in Artificial Immune Systems "(pdf)
3. Q Chen and U Aickelin " Movie Recommendation Systems Using An Artificial Immune System " (pdf)
Original on my blog
- Car Tips
- Cold start
- Introduction to hybrid systems
- Artificial immune systems and the effect of idiotypes
Reading various publications about data mining and recommendation systems, I accidentally stumbled upon one of the most interesting approaches to the implementation of such systems. It is based on the concept of an artificial immune system (IIS, Artificial immune system ), according to which some properties of the immune system of living organisms, including the ability to learn and memorize, are implemented in a computer system. A recommendation system uses a model that describes the concentration of antibodies that respond to a particular antigen. Of particular interest is the so-called effect idiotypes ( Idiotype ), showing that the concentration of antibodies depends not only on their similarity to the antigen, but also on the similarities with each other.
For those who are not familiar with biology, I will briefly explain the essence of the matter. An antigen is a substance that, when ingested, causes an immune system to respond. In response, it produces antibodies , a certain class of proteins that are used to identify and neutralize stimuli. In our case, the antigen is the user, and the antibodies are the objects with which you compare it. To make it easier to imagine, I suggest that we consider a collective filtering system, where other users are antibodies.
Mathematical Description
Now let's get down to business. An equation describing the concentration of antibodies proposed J. Doyne Farmer :
')

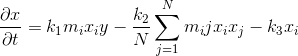
Where:
m i - the similarity between the antigen and antibody i,
x i and x j - the concentration of antibodies i and j, respectively,
y is the concentration of antigen,
m ij - the similarity between antibodies i and j,
k 1 - coefficient of stimulation
k 2 - the coefficient of suppression,
k 3 - the mortality rate
N is the number of antibodies.
Consider each addend separately:
- Stimulation of antibodies should not cause questions. This term increases the concentration of the antibody if it is appropriate for the antigen.
- Antibody suppression is much more interesting. It is in this term that the idiotype effect mentioned earlier lies. For a collective filtering system, it increases the result if the users with whom we compare the antigen to us are not only similar to it, but also have little resemblance to each other. This allows you to create a more diverse set of users.
- Mortality reduces the result if the absolute values of the first two terms are approximately equal. Thanks to him, antibodies that are neither good nor bad sweep themselves away.
Work principles
The algorithm of such a system is quite simple.
1. We take from the database the first antibody and calculate its concentration according to the described formula.
2. The result, obviously, can be both positive and negative, if it is below a certain minimum - discard the antibody and take the following.
3. We continue this cycle until the antibodies run out or the system does not stabilize , that is, if the result is almost unchanged over the last plus or minus ten iterations.
IIS has two main differences from other systems of recommendations:
- Another principle is the choice of compared objects. If in conventional collective filtering systems the most similar users are selected, then IIS adds also the effect of idiotypes, thanks to which the final selection is more diverse. This effect can be used not only to create a new collection, but also to improve existing ones.
- The method of calculating the rating itself is different. If in conventional systems it is just some kind of correlation coefficient, then in IIS this coefficient is multiplied by the resulting concentration.
Example
At the request of readers, I will give a simple example of using IIS. Suppose we have a correlation table of users A, B, C and Y obtained by some method. Our system works on the principle of collective filtering, so we need to find two users similar to user Y, and use their voices to further predict the voice of user Y In this example, I will not consider how we got this table and how we use the result in the future. Consider only how the effect of idiotypes will affect the choice of the users we need.
| A | B | C | Y | |
| A | one | 0.2 | 0.8 | 0.9 |
| B | 0.2 | one | 0.6 | 0.8 |
| C | 0.8 | 0.6 | one | 0.85 |
| Y | 0.9 | 0.8 | 0.85 | one |
For an ordinary system, users B and C will be the obvious choice, and they will be right too.
Let's see what IIS offers. Calculate the concentration for users B and C. Let the formula be in front of your eyes:
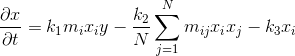
Take k 1 = 0.3, k 2 = 0.2, k 3 = 0.1, y = 1, since we need to select two users, N = 2. Then:
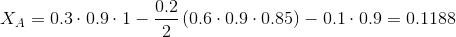
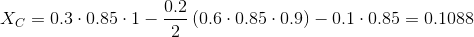
Let us assume that the minimum value of concentration accepted by us is 0.11. X C clearly does not fit into him, so we need to look for a replacement for him. Consider user B:
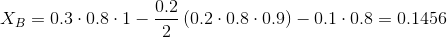
As you can see, despite the fact that its similarity with user Y is slightly less than user C, its concentration is noticeably greater, since B is less similar to A than C. So, as we replaced user C with B, we must recalculate and User A's concentration, because it depends on other users:

By calculating the concentration, we can accordingly adjust the similarity of users with user Y:
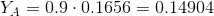
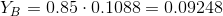

Conclusion
According to the published test results, the IIS actually give more accurate results than other systems, but the reason for their success is not in the influence of any particular factor from those considered above, but in their interaction. For details, I advise you to look into the sources:
1. Steve Cayzer and Uwe Aickelin " A Recommender System Based on the Immune Network " (pdf)
2. Steve Cayzer and Uwe Aickelin " On the Effects of Idiotypic Interactions for Recommendation
Communities in Artificial Immune Systems "(pdf)
3. Q Chen and U Aickelin " Movie Recommendation Systems Using An Artificial Immune System " (pdf)
Original on my blog
Source: https://habr.com/ru/post/59631/
All Articles