How computers play chess
The most interesting implementation of the chess program was shown yesterday at Habré.
After reading the comments, I came to the conclusion that the principle of operation of the most common algorithms of the game of chess, checkers and the like is not known to everyone.
At the same time, the task of creating a program that plays into something is rather trivial if there are ways of calculating some values and estimates specific to this particular game.
I’ll talk about alpha-beta cut-offs and the minimax method as applied to chess (in the literature one can also find more general terms such as the method of edges and estimates and the method of branches and boundaries)
At any moment of the game for each player there is a certain number of rules allowed by the moves. Suppose it of course. In response, the second player can also make a finite number of moves. If we exclude the possibility of looping the game, then the total number of positions and transitions between them is large, but of course. Chess rules are exactly that.
')
It would seem that simpler: they did a complete brute force and we know everything about the game; computer can not play.
However, the number of positions is so large that a complete analysis of the game is almost impossible (with the exception of the classic 3x3 daggers and games with similar rich strategies).
Therefore, in practice, the following is done :
1. Analytically, expertly or by the method of reasoning on precedents, the function of assessing the position on the board is constructed. This estimate is usually ranked on the axis: the more it is, the more profitable white is, the less, the more profitable black and, accordingly, less profitable white (the so-called zero-sum games).
2. Construct an incomplete tree of moves. The number of calculated half-lives is actually determined by the available computing resources (the attached program calculates 7 half-passes, which is rather modest for modern programs)
3. Some moderately intelligent analysis of the tree of possible moves is performed, during which deliberately non-optimal branches are cut off and more promising ones are deeply calculated. This is where the famous alpha-beta procedure is performed.
And now the same, but more formally and strictly (the presentation is mainly based on the article of D. Knut and R. Moore in the translation of Pavel Dubner ):
Legend :
p - position
f (p) is a numerical function that evaluates the gain of “our” player at the end of the game (these p positions are also called terminal)
F (p) is a numerical function that evaluates the gain of “our” player in a non-terminal position
We will proceed from the fact that the second player also acts in the best way for himself.
Then:
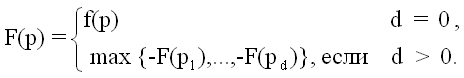
There is a subtle consideration, Knut and Moore formulated it very well, so I’ll just quote:
Full depth search :
This search is recursive and will work for a very long time, but is guaranteed to find the optimal strategy.
You can optimize the algorithm without considering those branches of the move tree that are obviously worse than the solution already found (this is called the branch and bound method).
The idea of the branch and bound method is implemented by the following algorithm :
This modification also finds the optimal solution.
In the case of analyzing a knowingly finite game tree, where all terminal vertices have estimates, you can enter not only the upper limit for the search, but also the lower one, still reducing the search space and saving resources.
The alpha beta cut-offs are implemented with the following code :
Such optimization still finds the best solution .
In practice, even in the most simple games, not to mention even chess, a complete search of the terminal positions cannot be organized. Therefore, there is a nontrivial task of an approximate assessment of the position. It is clear that the correct mate gives a lot of advantages to the position, but everything is also taken into account: the position of the pieces, the security of the king, numerical superiority, the possibility of castling. Depending on the details of the implementation, the robot may be too careful or, conversely, recklessly rush into exchanges.
The use of any evaluation functions deprives the algorithm of mathematical rigor. It will be as good as the evaluation function.
It is clear that the first function call F2 contains, as alpha and beta, infinity of a different sign.
Example of a move tree:

Additional explanations on the last figure here: Source
Another problem is the beginning of the game. Until the end is far, the prospects are foggy, nobody gives mats to put. Therefore, as a rule, libraries of investigated debuts are used. If the opponent does something unintelligible from the standpoint of chess tactics, the analyzer described above is turned on.
In principle, all of the above is relatively easy. My students after 2 courses in three weeks for three weeks piled these chess . There everything is done fairly well and there is room to grow.
After reading the comments, I came to the conclusion that the principle of operation of the most common algorithms of the game of chess, checkers and the like is not known to everyone.
At the same time, the task of creating a program that plays into something is rather trivial if there are ways of calculating some values and estimates specific to this particular game.
I’ll talk about alpha-beta cut-offs and the minimax method as applied to chess (in the literature one can also find more general terms such as the method of edges and estimates and the method of branches and boundaries)
At any moment of the game for each player there is a certain number of rules allowed by the moves. Suppose it of course. In response, the second player can also make a finite number of moves. If we exclude the possibility of looping the game, then the total number of positions and transitions between them is large, but of course. Chess rules are exactly that.
')
It would seem that simpler: they did a complete brute force and we know everything about the game; computer can not play.
However, the number of positions is so large that a complete analysis of the game is almost impossible (with the exception of the classic 3x3 daggers and games with similar rich strategies).
Therefore, in practice, the following is done :
1. Analytically, expertly or by the method of reasoning on precedents, the function of assessing the position on the board is constructed. This estimate is usually ranked on the axis: the more it is, the more profitable white is, the less, the more profitable black and, accordingly, less profitable white (the so-called zero-sum games).
2. Construct an incomplete tree of moves. The number of calculated half-lives is actually determined by the available computing resources (the attached program calculates 7 half-passes, which is rather modest for modern programs)
3. Some moderately intelligent analysis of the tree of possible moves is performed, during which deliberately non-optimal branches are cut off and more promising ones are deeply calculated. This is where the famous alpha-beta procedure is performed.
And now the same, but more formally and strictly (the presentation is mainly based on the article of D. Knut and R. Moore in the translation of Pavel Dubner ):
Legend :
p - position
f (p) is a numerical function that evaluates the gain of “our” player at the end of the game (these p positions are also called terminal)
F (p) is a numerical function that evaluates the gain of “our” player in a non-terminal position
We will proceed from the fact that the second player also acts in the best way for himself.
Then:
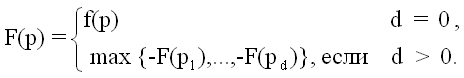
There is a subtle consideration, Knut and Moore formulated it very well, so I’ll just quote:
It should, however, be noted that it reflects the results of a very cautious strategy that is not necessarily good against bad players or players acting according to another principle of optimality. Suppose, for example, there are two moves in position p1 and p2, and p1 guarantees a draw (win 0) and does not make it possible to win, while p2 makes it possible to win if the opponent sees a very subtle winning move. In such a situation, we can prefer the risky move to p2, if only we are not sure that our opponent is omnipotent and omniscient. It is very possible that people win over chess programs in exactly this way.
Full depth search :
int F( void *p)
{
int res,i,t,d,m;
// ps ( d)
possibles(p, ps, &d);
if (!d) res=f(p) else
{
m = -infinity;
for (i=1;i<=d;i++)
{
t = -F(ps[i]);
if (t > m) m=t;
}
res = m;
}
return res
* This source code was highlighted with Source Code Highlighter .This search is recursive and will work for a very long time, but is guaranteed to find the optimal strategy.
You can optimize the algorithm without considering those branches of the move tree that are obviously worse than the solution already found (this is called the branch and bound method).
The idea of the branch and bound method is implemented by the following algorithm :
int F1( void *p, int bound)
{
int res,i,t,d,m;
// ps ( d)
possibles(p, ps, &d);
if (!d) res=f(p) else
{
m = -infinity;
for (i=1;(i<=d) && (m<bound);i++)
{
t = -F1(ps[i],-m);
if (t > m) m=t;
}
res = m;
}
return res;
}
* This source code was highlighted with Source Code Highlighter .This modification also finds the optimal solution.
In the case of analyzing a knowingly finite game tree, where all terminal vertices have estimates, you can enter not only the upper limit for the search, but also the lower one, still reducing the search space and saving resources.
The alpha beta cut-offs are implemented with the following code :
int F1( void *p, int alpha, int beta)
{
int res,i,t,d,m;
// ps ( d)
possibles(p, ps, &d);
if (!d) res=f(p) else
{
m = alpha;
for (i=1;(i<=d) && (m<beta);i++)
{
t = -F2(ps[i],-beta,-m);
if (t > m) m=t;
}
res = m;
}
return res;
}
* This source code was highlighted with Source Code Highlighter .Such optimization still finds the best solution .
In practice, even in the most simple games, not to mention even chess, a complete search of the terminal positions cannot be organized. Therefore, there is a nontrivial task of an approximate assessment of the position. It is clear that the correct mate gives a lot of advantages to the position, but everything is also taken into account: the position of the pieces, the security of the king, numerical superiority, the possibility of castling. Depending on the details of the implementation, the robot may be too careful or, conversely, recklessly rush into exchanges.
The use of any evaluation functions deprives the algorithm of mathematical rigor. It will be as good as the evaluation function.
It is clear that the first function call F2 contains, as alpha and beta, infinity of a different sign.
Example of a move tree:

Additional explanations on the last figure here: Source
Another problem is the beginning of the game. Until the end is far, the prospects are foggy, nobody gives mats to put. Therefore, as a rule, libraries of investigated debuts are used. If the opponent does something unintelligible from the standpoint of chess tactics, the analyzer described above is turned on.
In principle, all of the above is relatively easy. My students after 2 courses in three weeks for three weeks piled these chess . There everything is done fairly well and there is room to grow.
Source: https://habr.com/ru/post/51076/
All Articles