Classes of types, monads
The topic of today's article will be classes of types, some standard ones, syntactic sugar with their use, and a class of monads.
Classes introduce dynamic polymorphism, as well as interfaces in traditional imperative languages, and can also be used as replacements for functions overloading that is missing in Haskell.
I will tell you how to define a type class, its instances and how it is all arranged inside.
Previous articles:
Data Types, Pattern Matching and Functions
The basics
Suppose you have written your data type and want to write a comparison operator for it. The problem is that there is no overloading of functions in Haskell and therefore cannot be used for this purpose (==). Moreover, to invent a new name for each type is not an option.
But you can define a “compare” type class. Then, if your data type belongs to this class, values of this type can be compared.
Type
In a class, you can define a default function. For example, the functions
Now we’ll write a class instance for
We define one function
The same restrictions can be applied when declaring the class itself:
Classes are somewhat similar to interfaces - we declare functions for which we then provide implementations. Other functions can use these functions only if for some type there is such an implementation.
However, there are significant differences both in capabilities and in the implementation of the mechanism itself.
Since I already mentioned C ++, at the same time I would say that in the new C ++ 0x standard, concept and concept_map are the essence of type classes, but used at the compilation stage :)
But there is a drawback. How do we get a list of objects that, for example, belong to the class
There is a way, but it is non-standard. At the top of the file you need to add the appropriate GHC options:
And at the same time to determine for him an instance of the class
')
In the function that imposes restrictions on the type, a hidden parameter is passed (for each class and type - its own) - a dictionary with all the necessary functions.
In fact, an
To make it easier to understand, I just give a pseudo-implementation for the
Enum - listing. Defines functions for getting next / previous value, as well as value by number.
Used in syntactic sugar for lists
Show - conversion to a string, the main function
Used, for example, by the interpreter to display values.
Read - conversion from string, the main function
I don’t know why they chose to return the value, rather than
Eq - comparison, operators
Ord - ordered types, operators
A more complete list of different classes can be found here .
Functor - functor, function
To be clear, I will give examples of the use of this function:
I will write more about I / O later, for now you can just remember that
In order not to define instances for newly written data types each time, Haskell can do this automatically for some classes.
The Monad class is a “calculation”, i.e. It allows you to describe how to combine calculations and results.
It is unlikely that I will write an article better than there are already written, so I will simply give links to the best (in my opinion) articles for understanding what these monads are for.
1. Monads - an article with SPbHUG about monads in Russian and with analogies in the usual imperative languages.
2. IO inside - an English article on input and output using monads
3. Yet Another Haskell Tutorial is a book on Haskel, in the Monads section it is very well written using the example of creating the Computation class, which is the essence of a monad.
Here I will write very briefly, so that you can then peep.
Suppose we want to describe sequential calculations, where each of the following depends on the results of the previous one (in some way not specified in advance). To do this, you can define the appropriate class, in which there must be at least two functions:
The second function takes 2 arguments:
1. a calculation that, when executed, will return a value of type
2. a function that takes a value of type
The result is a calculation that returns a value of type
Why all this may be necessary, I will show the example of the optional value
But after all, our language allows us to pass functions as arguments and return the same way, using:
You may notice that the type of the
In addition, syntactic sugar is defined for monads, which greatly simplifies their use:
The special syntax with an inverse arrow
1. do {e} -> e
do with a single calculation is the calculation itself, you do not need to combine
2. do {e; es} -> e >> do {es}
several consecutive calculations are connected by an operator
3. do {let decls; es} -> let decls in do {es}
inside do you can make additional declarations like
4. do {p <- e; es} -> let ok p = do {es}; ok _ = fail "..." in e >> = ok
if the result of the first calculation is used further, then the operator is used for the combination
In the latter case, such a construction is used because a sample can act as
If it matches, then the further calculation will be performed, otherwise an error with a string description will be returned.
The
What other monad instances are in the standard library?
State - calculations with a state. With the help of
The list is also a monad. Subsequent calculations apply to all previous results.
Continuations (continued) in Haskele - also a monad - Cont
You can read about the continuation on the Russian wiki and the English wiki and further on by links.
They deserve special attention, but I cannot fit everything, and they have no direct relation to monads.
A good article about the continuation in Scheme is in the user palm_mute in a live journal.
I / O is also implemented using monads. For example, the
those. any input-output function as if accepts a state of the world, and returns some result and a new state of the world, which is then used by subsequent functions.
Of course, this is just a mental representation.
Since, unlike lists and Maybe, we do not have constructors of type
(“Never” - this is loudly said, in fact there is
It is worth mentioning Monad transformers (monad transformers).
If we need a state, we can use
To do this, use the StateT transformer, which connects the
Let's look at an example of factorial, which we change so that it prints the battery
In addition to StateT, there is also a ListT (for the list).
Full list of monads and monad transformers .
For convenience, generic functions are defined over monads. Their names speak for themselves, most of them duplicate list functions, so I'll just list some of them and give this link.
(I do not undertake to translate this term)
List comprehensions allows you to construct lists in accordance with mathematical notation:
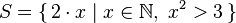
y may depend on x:
List comprehensions is also syntactic sugar and unfolds in (last example):
Next time I will try to answer all the questions, and then it will be possible to take up the implementation of the chat (or immediately, if there are few / no questions), so ask if it is not clear across all the articles.
Classes introduce dynamic polymorphism, as well as interfaces in traditional imperative languages, and can also be used as replacements for functions overloading that is missing in Haskell.
I will tell you how to define a type class, its instances and how it is all arranged inside.
Previous articles:
Data Types, Pattern Matching and Functions
The basics
Type Classes
Suppose you have written your data type and want to write a comparison operator for it. The problem is that there is no overloading of functions in Haskell and therefore cannot be used for this purpose (==). Moreover, to invent a new name for each type is not an option.
But you can define a “compare” type class. Then, if your data type belongs to this class, values of this type can be compared.
class MyEq a where
myEqual :: a -> a -> Bool
myNotEqual :: a -> a -> BoolMyEq is the name of the type class (like data types, it must begin with a capital letter), a is a type belonging to this class. A class can have several FooClass abc ( FooClass abc ), but in this case only one.Type
a belongs to the class MyEq , if corresponding functions are defined for it.In a class, you can define a default function. For example, the functions
myEqual and myNotEqual can be expressed through each other:myEqual xy = not ( myNotEqual xy )
myNotEqual xy = not ( myEqual xy )Now we’ll write a class instance for
Bool :instance MyEq Bool where
myEqual True True = True
myEqual False False = True
myEqual _ _ = Falseinstance , instead of a variable of type a in the definition of the class itself, we write the type for which the instance is defined, i.e. Bool .We define one function
myEqual and now we can check the result in the interpreter:ghci> myEqual True True
True
ghci> myNotEqual True False
True
ghci> :t myEqual
myEqual :: (MyEq a) => a -> a -> BoolmyEqual function imposes a constraint (constraints) on the type - it must belong to the class MyEq .The same restrictions can be applied when declaring the class itself:
class ( MyEq a ) => SomeClass a where
-- ...Classes are somewhat similar to interfaces - we declare functions for which we then provide implementations. Other functions can use these functions only if for some type there is such an implementation.
However, there are significant differences both in capabilities and in the implementation of the mechanism itself.
- As seen in the
myEqualfunction, it takes two values of typea, whereas the virtual function takes only one hidden parameterthis.
Even if we have aninstance MyEq Booland aninstance MyEq Int, a call to the functionmyEqual True 5will fail:
The compiler (interpreter) knows thatghci> myEqual True (5::Int)
<interactive>:1:14:
Couldn't match expected type `Bool' against inferred type `Int'
In the second argument of `myEqual', namely `(5::Int)'
In the expression: myEqual True (5 :: Int)
In the definition of `it': it = myEqual True (5 :: Int)
ghci>myEqualparameters must be of the same type and therefore prevents such attempts. - A class instance can be defined at any time, which is also very convenient. Inheritance from interfaces is specified when defining the class itself.
- The function may require that the data type belong to several classes at once:
How to do this, for example, in C ++ / C #? Create a compositefoo :: ( Eq a , Show a , Read a ) => a -> String -> StringIEquableShowableReadable? But you will not inherit from it. Pass the argument three times with coercion to different interfaces and assume inside the function that it is the same object, and the responsibility lies with the caller?
Since I already mentioned C ++, at the same time I would say that in the new C ++ 0x standard, concept and concept_map are the essence of type classes, but used at the compilation stage :)
But there is a drawback. How do we get a list of objects that, for example, belong to the class
Show (function show :: a -> String )?There is a way, but it is non-standard. At the top of the file you need to add the appropriate GHC options:
{-#
OPTIONS_GHC
-XExistentialQuantification
#-}
-- , , TAB' GHCdata ShowObj = forall a . Show a => ShowObj aAnd at the same time to determine for him an instance of the class
Show , so that he himself also belonged to him:instance Show ShowObj where
show ( ShowObj x ) = show xghci> [ShowObj 4, ShowObj True, ShowObj (ShowObj 'x')]
[4,True,'x']show function, the interpreter uses it, so you can be sure that everything works.')
How is all this implemented?
In the function that imposes restrictions on the type, a hidden parameter is passed (for each class and type - its own) - a dictionary with all the necessary functions.
In fact, an
instance is the definition of a dictionary instance for a particular type.To make it easier to understand, I just give a pseudo-implementation for the
Eq in Haskell and in C ++:-- class MyEq
data MyEq a = MyEq {
myEqual :: a -> a -> Bool ,
myNotEqual :: a -> a -> Bool }
-- instance MyEq Bool
myEqBool = MyEq {
myEqual = \ xy -> x == y ,
myNotEqual = \ xy -> not ( x == y ) }
-- foo :: (MyEq a) => a -> a -> Bool
foo :: MyEq a -> a -> a -> Bool
foo dict xy = ( myEqual dict ) xy
-- foo True False
fooResult = foo myEqBool True False#include <iostream> <br/>
<br/>
// class MyEq a <br/>
class MyEq<br/>
{ <br/>
public : <br/>
virtual ~MyEq ( ) throw ( ) { } <br/>
// void const *, <br/>
virtual bool unsafeMyEqual ( void const * x, void const * y ) const = 0 ;<br/>
virtual bool unsafeMyNotEqual ( void const * x, void const * y ) const = 0 ;<br/>
} ;<br/>
<br/>
// , <br/>
// <br/>
template < typename T > <br/>
class MyEqDictBase : public MyEq<br/>
{ <br/>
virtual bool unsafeMyEqual ( void const * x, void const * y ) const <br/>
{ return myEqual ( * static_cast < T const * > ( x ) , * static_cast < T const * > ( y ) ) ; } <br/>
virtual bool unsafeMyNotEqual ( void const * x, void const * y ) const <br/>
{ return myNotEqual ( * static_cast < T const * > ( x ) , * static_cast < T const * > ( y ) ) ; } <br/>
public : <br/>
virtual bool myEqual ( T const & x, T const & y ) const { return ! myNotEqual ( x, y ) ; } <br/>
virtual bool myNotEqual ( T const & x, T const & y ) const { return ! myEqual ( x, y ) ; } <br/>
} ;<br/>
<br/>
// . . <br/>
template < typename T > <br/>
class MyEqDict;<br/>
<br/>
// <br/>
template < typename T > <br/>
MyEqDict < T > makeMyEqDict ( ) { return MyEqDict < T > ( ) ; } <br/>
<br/>
// instance MyEq Bool <br/>
// MyEq bool <br/>
template <> <br/>
class MyEqDict < bool > : public MyEqDictBase < bool > <br/>
{ <br/>
public : <br/>
virtual bool myEqual ( bool const & l, bool const & r ) const { return l == r; } <br/>
} ;<br/>
<br/>
// <br/>
// , bool, Haskell' <br/>
bool fooDict ( MyEq const & dict, void const * x, void const * y ) <br/>
{ <br/>
return dict. unsafeMyNotEqual ( x, y ) ; // myNotEqual <br/>
} <br/>
<br/>
// <br/>
// foo :: (MyEq a) => a -> a -> Bool <br/>
template < typename T > <br/>
bool foo ( T const & x, T const & y ) <br/>
{ <br/>
return fooDict ( makeMyEqDict < T > ( ) , & x, & y ) ;<br/>
} <br/>
<br/>
int main ( ) <br/>
{ <br/>
std :: cout << foo ( true , false ) << std :: endl ; // 1 <br/>
std :: cout << foo ( false , false ) << std :: endl ; // 0 <br/>
return 0 ;<br/>
}Some standard classes and syntactic sugar
Enum - listing. Defines functions for getting next / previous value, as well as value by number.
Used in syntactic sugar for lists
[ 1 .. 10 ] , in fact, this means enumFromTo 1 10 , [ 1 , 3 .. 10 ] => enumFromThenTo 1 3 10Show - conversion to a string, the main function
show :: a -> String .Used, for example, by the interpreter to display values.
Read - conversion from string, the main function
read :: String -> a .I don’t know why they chose to return the value, rather than
Maybe a (optional value), to signal an error in a “clean” way, rather than a “dirty” exception.Eq - comparison, operators
( == ) and ( /= ) (as if crossed out equality sign)Ord - ordered types, operators
( < ) ( > ) ( <= ) ( >= ) . Requires type belonging to class Eq .A more complete list of different classes can be found here .
Functor - functor, function
fmap :: ( a -> b ) -> fa -> fb .To be clear, I will give examples of the use of this function:
ghci> fmap (+1) [1,2,3]
[2,3,4]
ghci> fmap (+1) (Just 6)
Just 7
ghci> fmap (+1) Nothing
Nothing
ghci> fmap reverse getLine
hello
"olleh"map , for the optional Maybe a value, the function ( + 1 ) is used if the value is present, and for I / O the function is applied to the result of this I / O.I will write more about I / O later, for now you can just remember that
getLine does not return a string, so you can’t directly apply reverse to it.In order not to define instances for newly written data types each time, Haskell can do this automatically for some classes.
data Test a = NoValue | Test aa deriving ( Show , Read , Eq , Ord )
data Color = Red | Green | Yellow | Blue | Black | Write deriving ( Show , Read , Enum , Eq , Ord )ghci> NoValue == ( Test 4 5 )
False
ghci> read "Test 5 6" :: Test Int
Test 5 6
ghci> ( Test 1 100 ) < ( Test 2 0 )
True
ghci> ( Test 2 100 ) < ( Test 2 0 )
False
ghci> [ Red .. Black ]
[ Red , Green , Yellow , Blue , Black ]Great and terrible monads
The Monad class is a “calculation”, i.e. It allows you to describe how to combine calculations and results.
It is unlikely that I will write an article better than there are already written, so I will simply give links to the best (in my opinion) articles for understanding what these monads are for.
1. Monads - an article with SPbHUG about monads in Russian and with analogies in the usual imperative languages.
2. IO inside - an English article on input and output using monads
3. Yet Another Haskell Tutorial is a book on Haskel, in the Monads section it is very well written using the example of creating the Computation class, which is the essence of a monad.
Here I will write very briefly, so that you can then peep.
Suppose we want to describe sequential calculations, where each of the following depends on the results of the previous one (in some way not specified in advance). To do this, you can define the appropriate class, in which there must be at least two functions:
class Computation c where
return :: a -> ca
bind :: ca -> ( a -> cb ) -> cbThe second function takes 2 arguments:
1. a calculation that, when executed, will return a value of type
a2. a function that takes a value of type
a and returns a new calculation that returns a value of type bThe result is a calculation that returns a value of type
b .Why all this may be necessary, I will show the example of the optional value
data Maybe a = Just a | NothingNothing . Then, using them directly, we risk getting such a weak code:Those. instead of simply calling these functions in sequence, you have to check the value each time.funOnMaybes x =
case functionMayFail1 x of
Nothing -> Nothing -- ,
Just x1 -> -- , ,
case functionMayFail2 x1 of
Nothing -> Nothing -- ( "")
Just x2 -> --
But after all, our language allows us to pass functions as arguments and return the same way, using:
combineMaybe :: Maybe a -> ( a -> Maybe b ) -> Maybe b
combineMaybe Nothing _ = Nothing
combineMaybe ( Just x ) f = fxcombineMaybe function accepts an optional value and function, and returns the result of applying this function to an optional value, or failure.funOnMaybes function:Or, using the fact that the function can be called infix:funOnMaybes x = combineMaybe ( combineMaybe x functionMayFail1 ) functionMayFail2 --...
funOnMaybes x = x `combineMaybe` functionMayFail1 `combineMaybe` functionMayFail2 --...
You may notice that the type of the
combineMaybe function exactly repeats the type of bind , only Maybe stands instead of c .instance Computation Maybe where
return x = Just x
bind Nothing f = Nothing
bind ( Just x ) f = fxMaybe monad is defined to, only bind is called there ( >>= ) , plus there is an additional operator ( >> ) that does not use the result of the previous computation.In addition, syntactic sugar is defined for monads, which greatly simplifies their use:
funOnMaybes x = do
x1 <- functionMayFail1 x
x2 <- functionMayFail2 x1
if x2 == (0)
then return (0)
else do
x3 <- functionMayFail3 x2
return ( x1 + x3 )do inside and then . do is just syntactic sugar, which combines several calculations into one, and since in the then branch there is a calculation and so is one ( return (0) ) , then do is not needed there; in the else branch, the calculations are two in a row, and in order to combine them, you need to use do again.The special syntax with an inverse arrow
(<-) converted very simply:1. do {e} -> e
do with a single calculation is the calculation itself, you do not need to combine
2. do {e; es} -> e >> do {es}
several consecutive calculations are connected by an operator
( >> )3. do {let decls; es} -> let decls in do {es}
inside do you can make additional declarations like
let ... in4. do {p <- e; es} -> let ok p = do {es}; ok _ = fail "..." in e >> = ok
if the result of the first calculation is used further, then the operator is used for the combination
( >>= )In the latter case, such a construction is used because a sample can act as
p , which may not coincide.If it matches, then the further calculation will be performed, otherwise an error with a string description will be returned.
The
fail function is another additional function in the monad, which generally has no relation to the concept of monads.What other monad instances are in the standard library?
State - calculations with a state. With the help of
get/put functions that are aware of the internal structure of the State , it is possible to get and set state.import Control . Monad . State
fact' :: Int -> State Int Int -- - Int, - Int
fact' 0 = do
acc <- get --
return acc --
fact' n = do
acc <- get --
put ( acc * n ) -- n
fact' ( n - 1 ) --
fact :: Int -> Int
fact n = fst $ runState ( fact' n ) 1 -- - 1
runState evaluates a function with a state, returns a tuple with a result and an altered state. We only need the result, so fst .The list is also a monad. Subsequent calculations apply to all previous results.
dummyFun contents = do
l <- lines contents --
if length l < 3 then fail "" -- 3
else do
w <- words l --
return w --ghci> dummyFun "line1\nword1 word2 word3\n \n \nline5"
["line1","word1","word2","word3","line5"]Continuations (continued) in Haskele - also a monad - Cont
You can read about the continuation on the Russian wiki and the English wiki and further on by links.
They deserve special attention, but I cannot fit everything, and they have no direct relation to monads.
A good article about the continuation in Scheme is in the user palm_mute in a live journal.
I / O is also implemented using monads. For example, the
getLine function getLine :getLine :: IO StringIO can be understood as:getLine :: World -> ( String , World )World is the state of the worldthose. any input-output function as if accepts a state of the world, and returns some result and a new state of the world, which is then used by subsequent functions.
Of course, this is just a mental representation.
Since, unlike lists and Maybe, we do not have constructors of type
IO , we will never be able to parse the result of type IO String into its components, but will only have to use it in other calculations, thus ensuring that the use of I / O will be reflected in type of function.(“Never” - this is loudly said, in fact there is
unsafePerformIO :: IO a -> a , but that's unsafe, to be used only with an understanding of the matter and when it is absolutely necessary. I personally have never used it).It is worth mentioning Monad transformers (monad transformers).
If we need a state, we can use
State , if I / O is IO . But what if our function wants to have states and still perform input and output?To do this, use the StateT transformer, which connects the
State and another monad. To perform calculations in this other monad, use the lift function.Let's look at an example of factorial, which we change so that it prints the battery
import Control . Monad . State
fact' :: Int -> StateT Int IO Int -- IO
fact' 0 = do
acc <- get
return acc
fact' n = do
acc <- get
lift $ print acc -- print acc - IO (), lift
put ( acc * n )
fact' ( n - 1 )
fact :: Int -> IO Int -- IO , :)
fact n = do
( r , _ ) <- runStateT ( fact' n ) 1
return r
ghci> fact 5
1
5
20
60
120
120In addition to StateT, there is also a ListT (for the list).
Full list of monads and monad transformers .
For convenience, generic functions are defined over monads. Their names speak for themselves, most of them duplicate list functions, so I'll just list some of them and give this link.
sequence :: Monad m => [ ma ] -> m [ a ]
--
mapM f = sequence . map f
forM = flip mapM
-- forM [1..10] $ \i -> print i
forever :: Monad m => ma -> mb -- ,
filterM :: Monad m => ( a -> m Bool ) -> [ a ] -> m [ a ] -- filter
foldM :: Monad m => ( a -> b -> ma ) -> a -> [ b ] -> ma -- foldl
when :: Monad m => Bool -> m () -> m () -- if elseList comprehensions
(I do not undertake to translate this term)
List comprehensions allows you to construct lists in accordance with mathematical notation:
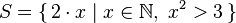
ghci> take 5 $ [ 2 * x | x <- [ 1 .. ] , x ^ 2 > 3 ]
[ 4 , 6 , 8 , 10 , 12 ]
ghci> [ ( x , y ) | x <- [ 1 .. 3 ] , y <- [ 1 .. 3 ] ]
[ ( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) , ( 2 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 1 ) , ( 3 , 2 ) , ( 3 , 3 ) ]y may depend on x:
ghci> [ x + y | x <- [ 1 .. 4 ] , y <- [ 1 .. x ] , even x ]
[ 3 , 4 , 5 , 6 , 7 , 8 ]List comprehensions is also syntactic sugar and unfolds in (last example):
do
x <- [ 1 .. 4 ]
y <- [ 1 .. x ]
True <- return ( even x )
return ( x + y )Next time I will try to answer all the questions, and then it will be possible to take up the implementation of the chat (or immediately, if there are few / no questions), so ask if it is not clear across all the articles.
Source: https://habr.com/ru/post/51046/
All Articles