Parser math expressions
Thank you all! The article gained the necessary number of advantages and the author joins us! Here it is: elw00d
I present to the attention of fellow donetchikov a library of my own writing, with the help of which one can easily handle simple mathematical functions, translating them from the string form of infix notation into a processed representation composed in postfix notation, and back. What can it be needed for?
For example, you can write an application that accepts user input as a string, analyzes syntax correctness, calculates its value at specified points, optimizes the entered expression, minimizing the number of operations required for the calculation, and can produce the result as a string that represents the correct string representation of the optimized function. As specific applications, various specialized calculators (including those built like programmable ones), applications used to build graphs or other reports that require defining initial functions, or as an original tool for building anti-spam / automatic registrations can be mentioned.
It all started with the fact that I saw an application written by some superprogrammer for laboratory work on numerical optimization methods. The input of the original function in it was organized in the following original way: the user (== student) entered the function, and the program generated the source code and started the next-line Delphi compiler to get the DLL. Then the DLL that appeared appeared in the program and the graph was built according to the function. Laughing a little at the developer’s resourcefulness, I thought, how could it be possible to organize similar functionality without using such a thick “plug-in” as the Delphi compiler? As a result, I got an idea to write my own parser for such tasks. That's what came out of this idea.
At the moment, the following functionality has been implemented and tested:
')
1. Analysis of lines of expressions composed of standard mathematical operators +, -, /, *, functions
sin, cos, brackets. It supports variables with any names that are acceptable for the syntax
analyzer (consist of letters and numbers, must begin with a letter).
An example of such an expression is the string
“ -4 + 5.5 * sin (1/3) * (2 + 5) ”.
To calculate this expression, you need to write code:
2. The ability to quickly add the necessary functions and operators by simply configuring the xml-config library. Functions with multiple arguments are supported, for example, you can define your own signature of the myfunc function, which takes 2 parameters. In the expression, it can be called like this: “myfunc (12, x)”. Here x is a variable, its value must be transferred to the calculator during the calculation.
Operators with more than two operands are also supported (as an example, the library has already defined the ternary operator?: Which gives the value of the second or third operand, depending on the sign of the first operand.
All operations (operators and functions) are characterized by a signature (a symbolic representation by which occurrences in the source string are searched for), priority, the number of operands, and a calculator class that will be used to calculate this operation. The class calculator implements the interface
Thus, in order to add a new operator or function, you need to define a class-calculator for this function and add an entry to Operations.xml of the form
During initialization, the library will load the types necessary for processing the added function and match this operation with an instance of the selected calculator class. During the calculation, the corresponding Calculate () function with the passed parameters will be called.
3. The ability to optimize the compiled expression by predicting constants. For example, the expression (3 + 5) / x can be reduced to the form 8 / x. The resulting expression can be used in calculations instead of the original one, and even output to the user as a slightly simplified version of its function. The optimization algorithm can be improved by adding new features (if someone, of course, lights up with such an idea).
4. Ability to control the intermediate stages of the transformation of expressions. From string to a sequence of signatures and operands, then to the reverse Polish record from operands and operations, and vice versa. In general, possible transitions are reflected in the following diagram:
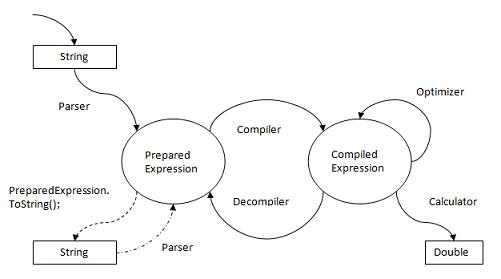
String and Double are primitive types, expression processing begins with them, and usually ends with them.
Prepared Expression - consists of a set of elements, each of which is either a constant, or a variable name, or a separator, such as a bracket or comma, or a string signature of the operation. For example, the expression (a + b) / 3 will be a set of '(', “a”, “+”, “b”, ')', “/”, 3. The number 3 is no longer in string form and Double.
Compiled Expression is a set of operands and operations on them in postfix notation, that is, exactly what the calculator feeds on. It is an array of operands (either a constant or a variable name) and operations (either an operator or a function). Calculator, receiving this expression as an input, works with it according to a simple algorithm, by turns extracting operands and information about operations and performing sequential calculations in the operand stack.
5. It is assembled both under the .NET Framework 3.5 and under .NET 2.0. Attached are nant scripts to automate
builds can be used with Visual Studio.
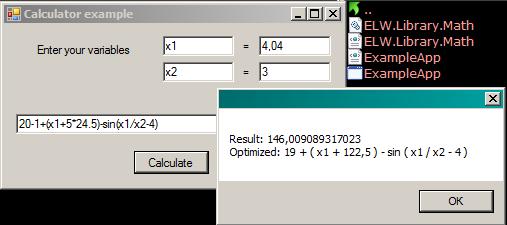
Screenshot of the library example:
Epilogue.
So far, the possibilities are not too great, however, they are sufficient to play around with the invention of their own operators, with changing the priority of operator calculations, or for the primitive optimization of mathematical expressions.
Download library sources + test application
Things to think about:
ru.wikipedia.org/wiki/Reverse_pole_record
msdn.microsoft.com/en-ru/library/ms139741.aspx
I present to the attention of fellow donetchikov a library of my own writing, with the help of which one can easily handle simple mathematical functions, translating them from the string form of infix notation into a processed representation composed in postfix notation, and back. What can it be needed for?
For example, you can write an application that accepts user input as a string, analyzes syntax correctness, calculates its value at specified points, optimizes the entered expression, minimizing the number of operations required for the calculation, and can produce the result as a string that represents the correct string representation of the optimized function. As specific applications, various specialized calculators (including those built like programmable ones), applications used to build graphs or other reports that require defining initial functions, or as an original tool for building anti-spam / automatic registrations can be mentioned.
It all started with the fact that I saw an application written by some superprogrammer for laboratory work on numerical optimization methods. The input of the original function in it was organized in the following original way: the user (== student) entered the function, and the program generated the source code and started the next-line Delphi compiler to get the DLL. Then the DLL that appeared appeared in the program and the graph was built according to the function. Laughing a little at the developer’s resourcefulness, I thought, how could it be possible to organize similar functionality without using such a thick “plug-in” as the Delphi compiler? As a result, I got an idea to write my own parser for such tasks. That's what came out of this idea.
At the moment, the following functionality has been implemented and tested:
')
1. Analysis of lines of expressions composed of standard mathematical operators +, -, /, *, functions
sin, cos, brackets. It supports variables with any names that are acceptable for the syntax
analyzer (consist of letters and numbers, must begin with a letter).
An example of such an expression is the string
“ -4 + 5.5 * sin (1/3) * (2 + 5) ”.
To calculate this expression, you need to write code:
// PreparedExpression preparedExpression = ToolsHelper.Parser.Parse( "-4+5.5*sin(1/3)*(2+5)" ); CompiledExpression compiledExpression = ToolsHelper.Compiler.Compile(preparedExpression); // , // , List <VariableValue> variables = new List <VariableValue>(); // double res = ToolsHelper.Calculator.Calculate(compiledExpression, variables); * This source code was highlighted with Source Code Highlighter .
// PreparedExpression preparedExpression = ToolsHelper.Parser.Parse( "-4+5.5*sin(1/3)*(2+5)" ); CompiledExpression compiledExpression = ToolsHelper.Compiler.Compile(preparedExpression); // , // , List <VariableValue> variables = new List <VariableValue>(); // double res = ToolsHelper.Calculator.Calculate(compiledExpression, variables); * This source code was highlighted with Source Code Highlighter .// PreparedExpression preparedExpression = ToolsHelper.Parser.Parse( "-4+5.5*sin(1/3)*(2+5)" ); CompiledExpression compiledExpression = ToolsHelper.Compiler.Compile(preparedExpression); // , // , List <VariableValue> variables = new List <VariableValue>(); // double res = ToolsHelper.Calculator.Calculate(compiledExpression, variables); * This source code was highlighted with Source Code Highlighter .// PreparedExpression preparedExpression = ToolsHelper.Parser.Parse( "-4+5.5*sin(1/3)*(2+5)" ); CompiledExpression compiledExpression = ToolsHelper.Compiler.Compile(preparedExpression); // , // , List <VariableValue> variables = new List <VariableValue>(); // double res = ToolsHelper.Calculator.Calculate(compiledExpression, variables); * This source code was highlighted with Source Code Highlighter .// PreparedExpression preparedExpression = ToolsHelper.Parser.Parse( "-4+5.5*sin(1/3)*(2+5)" ); CompiledExpression compiledExpression = ToolsHelper.Compiler.Compile(preparedExpression); // , // , List <VariableValue> variables = new List <VariableValue>(); // double res = ToolsHelper.Calculator.Calculate(compiledExpression, variables); * This source code was highlighted with Source Code Highlighter .// PreparedExpression preparedExpression = ToolsHelper.Parser.Parse( "-4+5.5*sin(1/3)*(2+5)" ); CompiledExpression compiledExpression = ToolsHelper.Compiler.Compile(preparedExpression); // , // , List <VariableValue> variables = new List <VariableValue>(); // double res = ToolsHelper.Calculator.Calculate(compiledExpression, variables); * This source code was highlighted with Source Code Highlighter .// PreparedExpression preparedExpression = ToolsHelper.Parser.Parse( "-4+5.5*sin(1/3)*(2+5)" ); CompiledExpression compiledExpression = ToolsHelper.Compiler.Compile(preparedExpression); // , // , List <VariableValue> variables = new List <VariableValue>(); // double res = ToolsHelper.Calculator.Calculate(compiledExpression, variables); * This source code was highlighted with Source Code Highlighter .// PreparedExpression preparedExpression = ToolsHelper.Parser.Parse( "-4+5.5*sin(1/3)*(2+5)" ); CompiledExpression compiledExpression = ToolsHelper.Compiler.Compile(preparedExpression); // , // , List <VariableValue> variables = new List <VariableValue>(); // double res = ToolsHelper.Calculator.Calculate(compiledExpression, variables); * This source code was highlighted with Source Code Highlighter .// PreparedExpression preparedExpression = ToolsHelper.Parser.Parse( "-4+5.5*sin(1/3)*(2+5)" ); CompiledExpression compiledExpression = ToolsHelper.Compiler.Compile(preparedExpression); // , // , List <VariableValue> variables = new List <VariableValue>(); // double res = ToolsHelper.Calculator.Calculate(compiledExpression, variables); * This source code was highlighted with Source Code Highlighter .// PreparedExpression preparedExpression = ToolsHelper.Parser.Parse( "-4+5.5*sin(1/3)*(2+5)" ); CompiledExpression compiledExpression = ToolsHelper.Compiler.Compile(preparedExpression); // , // , List <VariableValue> variables = new List <VariableValue>(); // double res = ToolsHelper.Calculator.Calculate(compiledExpression, variables); * This source code was highlighted with Source Code Highlighter .
2. The ability to quickly add the necessary functions and operators by simply configuring the xml-config library. Functions with multiple arguments are supported, for example, you can define your own signature of the myfunc function, which takes 2 parameters. In the expression, it can be called like this: “myfunc (12, x)”. Here x is a variable, its value must be transferred to the calculator during the calculation.
Operators with more than two operands are also supported (as an example, the library has already defined the ternary operator?: Which gives the value of the second or third operand, depending on the sign of the first operand.
All operations (operators and functions) are characterized by a signature (a symbolic representation by which occurrences in the source string are searched for), priority, the number of operands, and a calculator class that will be used to calculate this operation. The class calculator implements the interface
* This source code was highlighted with Source Code Highlighter .
- public interface IOperationCalculator {
- /// <summary>
- /// Returns a result of operation called.
- /// </ summary>
- double Calculate ( params double [] parameters);
- }
- }
Thus, in order to add a new operator or function, you need to define a class-calculator for this function and add an entry to Operations.xml of the form
* This source code was highlighted with Source Code Highlighter .
- < operation name = "sinus" operands = "1" kind = "function" >
- < signatures >
- < signature number = "1" value = "sin" />
- </ signatures >
- < calculator type = "ELW.Library.Math.Calculators.Standard.CalculatorSinus, ELW.Library.Math" />
- </ operation >
During initialization, the library will load the types necessary for processing the added function and match this operation with an instance of the selected calculator class. During the calculation, the corresponding Calculate () function with the passed parameters will be called.
3. The ability to optimize the compiled expression by predicting constants. For example, the expression (3 + 5) / x can be reduced to the form 8 / x. The resulting expression can be used in calculations instead of the original one, and even output to the user as a slightly simplified version of its function. The optimization algorithm can be improved by adding new features (if someone, of course, lights up with such an idea).
4. Ability to control the intermediate stages of the transformation of expressions. From string to a sequence of signatures and operands, then to the reverse Polish record from operands and operations, and vice versa. In general, possible transitions are reflected in the following diagram:

String and Double are primitive types, expression processing begins with them, and usually ends with them.
Prepared Expression - consists of a set of elements, each of which is either a constant, or a variable name, or a separator, such as a bracket or comma, or a string signature of the operation. For example, the expression (a + b) / 3 will be a set of '(', “a”, “+”, “b”, ')', “/”, 3. The number 3 is no longer in string form and Double.
Compiled Expression is a set of operands and operations on them in postfix notation, that is, exactly what the calculator feeds on. It is an array of operands (either a constant or a variable name) and operations (either an operator or a function). Calculator, receiving this expression as an input, works with it according to a simple algorithm, by turns extracting operands and information about operations and performing sequential calculations in the operand stack.
5. It is assembled both under the .NET Framework 3.5 and under .NET 2.0. Attached are nant scripts to automate
builds can be used with Visual Studio.
Screenshot of the library example:

Epilogue.
So far, the possibilities are not too great, however, they are sufficient to play around with the invention of their own operators, with changing the priority of operator calculations, or for the primitive optimization of mathematical expressions.
Download library sources + test application
Things to think about:
ru.wikipedia.org/wiki/Reverse_pole_record
msdn.microsoft.com/en-ru/library/ms139741.aspx
Source: https://habr.com/ru/post/50158/
All Articles