Hierarchical data structures and performance
Introduction
In my previous article, I gave a brief overview of the basic storage models of hierarchical structures in relational databases. As it should be, for many readers the question has become an edge about the performance of the presented algorithms.
In this article I will try to lift the veil over this burning issue, and in the next I promise to touch on the issues of optimization and the search for non-standard solutions.
')
Training
So, testing. Like any other testing, ours also requires certain actions to prepare, analyze, develop goals and an action plan.
In fact, the goal is to conduct a series of stress tests of different algorithms on different data volumes. It would also be nice to get rid of tests on several different hardware platforms, but, alas, the author cannot do this (time and money are to blame for everything).
Naturally, it would be good to conduct tests of the most important and significant operations that are usually performed on various trees. After quite a long thought it was decided to stop at the following list of operations to be tested:
- Selection of the entire tree
- Sampling the path to a given node
- Sampling branches of a given node
- Search for the parent of the specified node
- Search for heirs of a given node
- Adding a new node to the end of the specified parent node
- Moving a node (or, in other words, changing the parent)
- Deleting a node (and the entire branch under it)
It should be noted that we are approaching these operations to combat conditions, i.e. the input data for us will be the identifiers of the nodes and their parents. This will allow not to become attached to specific implementations of each of the algorithms.
We further specify that we are interested in the performance of pure SQL, so we will take measurements solely on its work.
The author does not claim to be complete of the stated list of operations. Perhaps, someone will remember about the operations of searching for neighbors of a node or selecting all the sheets of a tree, and even in a given branch - please, everyone has the right to expand and supplement this experiment. For the time being, I’ll focus on the basic, in my opinion, basic minimal functionality.
Now I want to dwell in more detail on the implementation of the functions themselves, tests on which will be carried out in the future. But, if you are only interested in bare figures and facts, you can proceed to the next section of the article.
Not all of the declared functions have trivial solutions in different methods, especially on pure SQL. For example, selecting a branch in an AL tree is a purely recursive task. But is it worth doing this at the SQL level? ..
In general, several points should be considered:
- DBMS on which tests are made - MySQL version 5.0.x. Engine - InnoDB (suitable for implementing cascading operations for AL-Tree at the database level).
- Sampling requests are executed with the SQL_NO_CACHE flag to estimate the “net” cost of executing queries.
- Trees of different types have the same physical structure of nodes (ie, a tree of the same type is randomly created, and the rest of the trees are built from the first).
- Algorithms Nested Set and Materialized Path were strengthened by the level field, which stores the nesting level of the current node in the tree. In particular, we can say that this allows us to increase, for example, the sampling efficiency of the heirs of a node in the MP tree by more than 100 times! In fact, without this field, these algorithms, in a sense, lose their appeal. Therefore, we can speak not so much about their tuning when adding this field, but about the necessary condition for their functioning. Thus, the structure of our test database is as follows:
-- Adjacency List Tree Structure
CREATE TABLE `al_tree` (
`id` bigint(20) NOT NULL auto_increment,
`parent_id` bigint(20) default NULL ,
`name` varchar (50) NOT NULL ,
PRIMARY KEY (`id`),
KEY `fk_tree_tree` (`parent_id`),
CONSTRAINT `fk_tree_tree` FOREIGN KEY (`parent_id`) REFERENCES `al_tree` (`id`) ON DELETE CASCADE ON UPDATE CASCADE
) ENGINE=InnoDB DEFAULT CHARSET=utf8
-- Nested Set Tree Structure
CREATE TABLE `ns_tree` (
`id` bigint(20) NOT NULL auto_increment,
`name` varchar (50) NOT NULL ,
`lft` bigint(20) NOT NULL ,
`rgt` bigint(20) NOT NULL ,
` level ` bigint(20) NOT NULL ,
PRIMARY KEY (`id`),
KEY `nslrl_idx` (`lft`,`rgt`,` level `)
) ENGINE=InnoDB DEFAULT CHARSET=utf8
-- Materialized Path Tree Structure
CREATE TABLE `mp_tree` (
`id` bigint(20) NOT NULL auto_increment,
`name` varchar (50) NOT NULL ,
` path ` varchar (100) NOT NULL ,
` level ` int (11) NOT NULL ,
PRIMARY KEY (`id`),
KEY `mpp_idx` (` path `)
) ENGINE=InnoDB DEFAULT CHARSET=utf8
* This source code was highlighted with Source Code Highlighter .- To work with the Nested Set and Materialized Path trees, functions and procedures were written at the database level to simplify the routine operations of working with trees. In particular, the functions STRFIND, REPLACE_PATH and the procedures MOVE_NODE_NS, MOVE_NODE_MP, REMOVE_NODE_MP are added:
STRFIND (str, delimtr)
--
-- delimtr str.
--
-- MATERIALIZED PATH.
-- (- )
--
-- @param str VARCHAR(255) -
-- @param delimtr CHAR(1) -
-- @return INT - -
--
CREATE FUNCTION `STRFIND`(str VARCHAR (255), delimtr CHAR (1)) RETURNS INT
BEGIN
DECLARE _cnt INT ;
DECLARE _start INT ;
SET _cnt = -1;
SET _start = 1;
WHILE _start > 0 DO
SET _start = LOCATE( delimtr, str);
SET str = SUBSTRING ( str, _start + 1);
SET _cnt = _cnt + 1;
END WHILE ;
RETURN _cnt;
END
* This source code was highlighted with Source Code Highlighter .REPLACE_PATH (_str, _match, _replace)
--
-- _str
-- _match _replace,.
-- _match _str
--
-- MATERIALIZED PATH .
--
-- @param _str VARCHAR(255) -
-- @param _match VARCHAR(255) -
-- @param _replace VARCHAR(255) -
-- @return VARCHAR(255) -
--
CREATE FUNCTION `REPLACE_PATH`( _str VARCHAR (255), _match VARCHAR (255), _replace VARCHAR (255)) RETURNS VARCHAR (255)
BEGIN
IF _str LIKE CONCAT(_match, '%' ) THEN
RETURN CONCAT( _replace, SUBSTRING ( _str, LENGTH(_match)+1, LENGTH(_str)));
END IF ;
RETURN _str;
END
* This source code was highlighted with Source Code Highlighter .The main difference of the above function from the built-in REPLACE is that it is guaranteed to change the specified string only if a match is found from the beginning of the string and makes changes only once.
MOVE_NODE_NS (node_id, parent_id)
--
-- NESTED SET
--
-- @param node_id - ,
-- @param parent_id -
--
CREATE PROCEDURE MOVE_NODE_NS( node_id BIGINT, parent_id BIGINT)
BEGIN
DECLARE done INT DEFAULT 0;
DECLARE c_id, c_lft, c_rgt, c_lvl, nWidth, nLeft, nRight, dtKey, nLvl, pRight, addLvl, addKey BIGINT;
DECLARE c_name VARCHAR (50);
-- ,
--
DECLARE mvBranch CURSOR FOR
SELECT id, name, lft - dtKey, rgt - dtKey, level - nLvl FROM ns_tree
WHERE lft >= nLeft AND rgt <= nRight;
DECLARE CONTINUE HANDLER FOR NOT FOUND SET done = 1;
--
SELECT rgt - lft + 1, lft, rgt, lft - 1, level INTO nWidth, nLeft, nRight, dtKey, nLvl
FROM ns_tree WHERE id = node_id;
--
OPEN mvBranch;
--
DELETE FROM ns_tree WHERE lft BETWEEN nLeft AND nRight;
--
UPDATE ns_tree SET rgt = rgt - nWidth WHERE rgt > nRight;
UPDATE ns_tree SET lft = lft - nWidth WHERE lft > nRight;
--
SELECT rgt, level + 1 INTO pRight, addLvl FROM ns_tree WHERE id = parent_id;
SELECT MAX (node.rgt) INTO addKey FROM ns_tree node, ns_tree parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node. level = parent. level + 1 AND parent.id = parent_id;
-- ,
--
UPDATE ns_tree SET rgt = rgt + nWidth WHERE rgt >= pRight;
UPDATE ns_tree SET lft = lft + nWidth WHERE lft > pRight;
-- .
--
REPEAT
FETCH mvBranch INTO c_id, c_name, c_lft, c_rgt, c_lvl;
IF NOT done THEN
INSERT INTO ns_tree VALUES (c_id, c_name, c_lft + addKey, c_rgt + addKey, c_lvl + addLvl);
END IF ;
UNTIL done END REPEAT;
CLOSE mvBranch;
END
* This source code was highlighted with Source Code Highlighter .MOVE_NODE_MP (node_id, parent_id)
--
-- MATERIALIZED PATH
--
-- @param node_id - ,
-- @param parent_id -
--
CREATE PROCEDURE MOVE_NODE_MP( node_id BIGINT, parent_id BIGINT)
BEGIN
DECLARE done, m_cnt, m_rows, p_cnt, p_rows INT DEFAULT 0;
DECLARE c_id, p_id, n_pos, n_lvl, np_id, np_lvl, new_pos, dt_lvl, ch_id, ch_pos BIGINT;
DECLARE c_path, p_path, n_path, np_path, ch_path, new_path VARCHAR (100);
-- , ,
--
DECLARE mvBranch CURSOR FOR
SELECT SQL_CALC_FOUND_ROWS node.id, node. path FROM mp_tree node, mp_tree parent
WHERE node. path LIKE CONCAT(parent. path , '%' ) AND parent.id = node_id;
-- ,
-- ,
DECLARE pChildren CURSOR FOR
SELECT SQL_CALC_FOUND_ROWS node.id, node. path ,
CAST ( SUBSTRING (REVERSE(node. path ), 1, LOCATE( '.' , node. path )-1) AS UNSIGNED) as pos
FROM mp_tree node, mp_tree parent
WHERE node. path LIKE CONCAT(parent. path , '%' ) AND node. level = parent. level + 1
AND CAST ( SUBSTRING (REVERSE(node. path ), 1, LOCATE( '.' , node. path )-1) AS UNSIGNED) > n_pos
AND parent.id = p_id
ORDER BY pos;
DECLARE CONTINUE HANDLER FOR NOT FOUND SET done = 1;
--
SELECT path , CAST ( SUBSTRING (REVERSE( path ), 1, LOCATE( '.' , path )-1) AS UNSIGNED), level INTO n_path, n_pos, n_lvl FROM mp_tree
WHERE id = node_id;
SELECT parent.id, parent. path INTO p_id, p_path FROM mp_tree node, mp_tree parent
WHERE parent. path = SUBSTRING ( node. path , 1, (LENGTH(node. path ) - LOCATE( '.' , REVERSE(node. path ))))
AND node.id = node_id;
SELECT id, path , level INTO np_id, np_path, np_lvl FROM mp_tree WHERE id = parent_id;
--
-- :
SET dt_lvl = np_lvl - n_lvl + 1;
SELECT MAX ( CAST ( SUBSTRING (REVERSE(node. path ), 1, LOCATE( '.' , node. path )-1) AS UNSIGNED)) + 1
INTO new_pos FROM mp_tree node, mp_tree parent WHERE node. path LIKE CONCAT(parent. path , '%' )
AND node. level = parent. level + 1 AND parent.id = parent_id;
--
OPEN mvBranch;
SELECT FOUND_ROWS() INTO m_rows;
WHILE m_cnt < m_rows DO
FETCH mvBranch INTO c_id, c_path;
UPDATE mp_tree
SET path = REPLACE_PATH( path , n_path, CONCAT(np_path, '.' , new_pos)), level = level + dt_lvl WHERE id = c_id;
SET m_cnt = m_cnt + 1;
END WHILE ;
CLOSE mvBranch;
-- .
--
OPEN pChildren;
SELECT FOUND_ROWS() INTO p_rows;
WHILE p_cnt < p_rows DO
FETCH pChildren INTO ch_id, ch_path, ch_pos;
UPDATE mp_tree SET path = REPLACE_PATH( path , ch_path, CONCAT(p_path, '.' , ch_pos - 1)) WHERE path LIKE CONCAT( ch_path, '%' );
SET p_cnt = p_cnt + 1;
END WHILE ;
CLOSE pChildren;
END
* This source code was highlighted with Source Code Highlighter .REMOVE_NODE_MP (node_id)
--
-- MATERIALIZED PATH
--
-- @param node_id - ,
--
CREATE PROCEDURE REMOVE_NODE_MP( node_id BIGINT)
BEGIN
DECLARE n_pos, ch_id, p_id, ch_pos BIGINT;
DECLARE n_path, ch_path, p_path VARCHAR (100);
DECLARE done, p_cnt, p_rows INT DEFAULT 0;
-- ,
-- ,
DECLARE pChildren CURSOR FOR
SELECT SQL_CALC_FOUND_ROWS node.id, node. path ,
CAST ( SUBSTRING (REVERSE(node. path ), 1, LOCATE( '.' , node. path )-1) AS UNSIGNED) as pos
FROM mp_tree node, mp_tree parent
WHERE node. path LIKE CONCAT(parent. path , '%' ) AND node. level = parent. level + 1
AND CAST ( SUBSTRING (REVERSE(node. path ), 1, LOCATE( '.' , node. path )-1) AS UNSIGNED) > n_pos
AND parent.id = p_id
ORDER BY pos;
DECLARE CONTINUE HANDLER FOR NOT FOUND SET done = 1;
--
SELECT path , CAST ( SUBSTRING (REVERSE( path ), 1, LOCATE( '.' , path )-1) AS UNSIGNED) INTO n_path, n_pos FROM mp_tree
WHERE id = node_id;
SELECT parent.id, parent. path INTO p_id, p_path FROM mp_tree node, mp_tree parent
WHERE parent. path = SUBSTRING ( node. path , 1, (LENGTH(node. path ) - LOCATE( '.' , REVERSE(node. path ))))
AND node.id = node_id;
--
DELETE FROM mp_tree WHERE path LIKE CONCAT( n_path, '%' );
--
OPEN pChildren;
SELECT FOUND_ROWS() INTO p_rows;
WHILE p_cnt < p_rows DO
FETCH pChildren INTO ch_id, ch_path, ch_pos;
UPDATE mp_tree SET path = REPLACE_PATH( path , ch_path, CONCAT(p_path, '.' , ch_pos - 1)) WHERE path LIKE CONCAT( ch_path, '%' );
SET p_cnt = p_cnt + 1;
END WHILE ;
CLOSE pChildren;
END
* This source code was highlighted with Source Code Highlighter .In fact, now all the details of the implementation are disclosed, this can be stopped and proceed to the issues of testing.
Testing
Testing was performed using a self-written console program with the following configuration:
Hardware:
CPU: Intel® Core (TM) 2 Duo CPU E7200 @ 2.53GHz 6Mb 64bit
RAM: 4 Gb
HD: 2 x 250Gb 7200rpm RAID 1
Software:
OS: Debian Linux 2.6.26-1-amd64 (64bit)
PHP-CLI: 5.2.6-5 with Suhosin-Patch 0.9.6.2
MySQL: 5.0.51a, for debian-linux-gnu (x86_64) using readline 5.2
Let's say this machine is a server that is far from being heavily loaded at the moment (about 100,000 fairly simple HTTP requests per day), which is almost negligible for this configuration.
You can download the program from here and try testing it on your machine (it works only in a Unix-like environment). Instructions for working with the program can be found in the downloaded distribution file in the README.TXT file.
During testing, 5 tree configurations were selected:
- 100 nodes and nesting level 5
- 1000 nodes and nesting level 10
- 10,000 knots and nesting level 20
- 100,000 nodes and nesting level 25
- 500,000 nodes and nesting level 30
These are trees, tests over which managed to be successfully completed. All tests were completed in less than 6 hours, while most of the time, naturally, took the last test with trees of half a million nodes.
The algorithm for creating trees works in such a way that the law of the distribution of nodes in a tree is about the following:

Where the abscissa is the identifiers of the nodes in ascending order, and the ordinate is the number of nodes in the branches of the node with the specified identifier.
In connection with this state of affairs, the following testing scheme was chosen. Per sample - an iterative step-by-step scheme for checking the functioning of the sampling algorithms on different parts of the tree. Iterations are organized in the following way:
id> 1 <10 - step 1 id> 10 <100 - step 10 id> 100 <1000 - step 100 id> 1000 <10000 - step 1000 id> 10000 <100000 - step 10000 id> 100000 - step 100000
This allows tracing the dependence of the search and sampling functions on the distribution law of nodes.
For the change functions, the scheme chosen is somewhat different. Since the change operations themselves for most algorithms are quite costly operations, it makes no sense to check them in an iterative way (the waiting time for testing completion increases too much). Therefore, the verification method is based on making changes in one of the largest nodes, which is located at the beginning of the tree. In addition, such a test will be performed once. In order to describe the overall picture and identify the range of problems - this is quite enough.
Analysis
So, tests are performed, data is collected. I believe that there is no point in throwing out in this article all the numbers that we got in the results. However, they are available for download as an archive . So everyone can look at them personally.
Where it will be more interesting to show empirically what these results are. Let's look at what some graphs look like for a tree with 100,000 nodes.
Everything below is counted and specified in seconds.

Fig. 1. Selection of the entire tree
The following graphs show the dependence of the fluctuations of the sample functions on the search in different parts of the tree. In fact, the numbers on the y-axis indicate the steps discussed above.
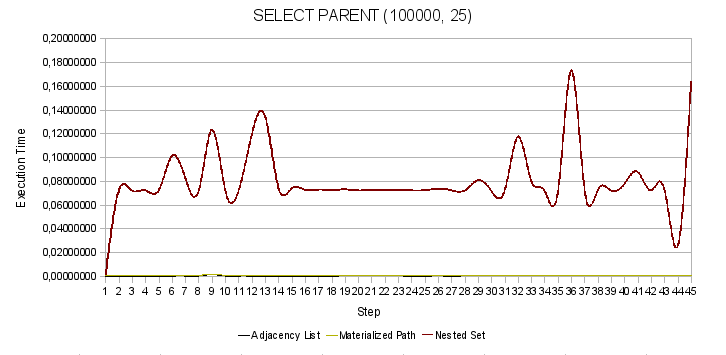
Fig. 2. Search for parent node
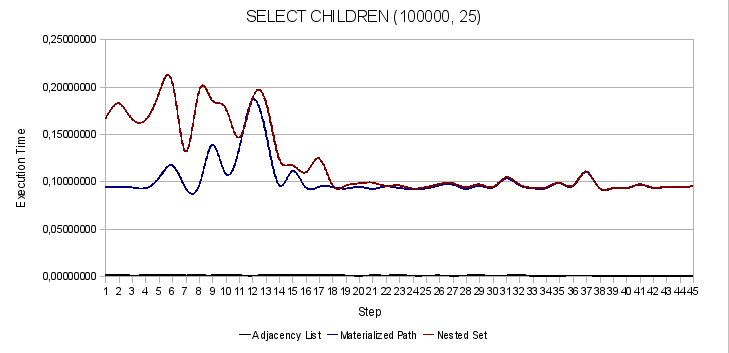
Fig. 3. Search for heirs of a given node
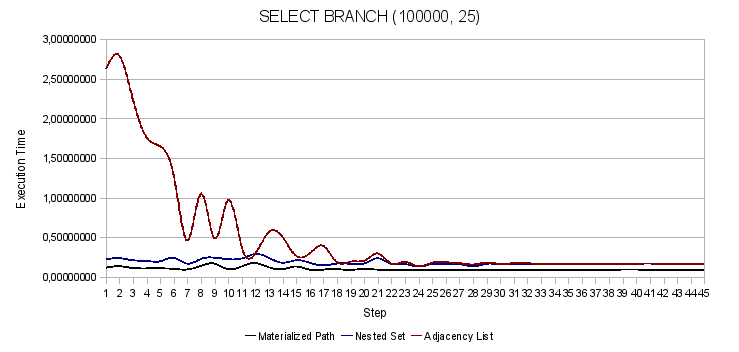
Fig. 4. Selection of the entire branch of a given node
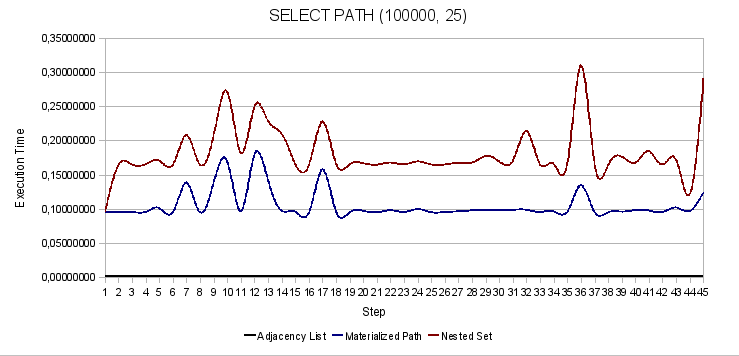
Fig. 5. Search for the complete path from the root to the given node
The following illustrates the function changes that were carried out on trees of various types.
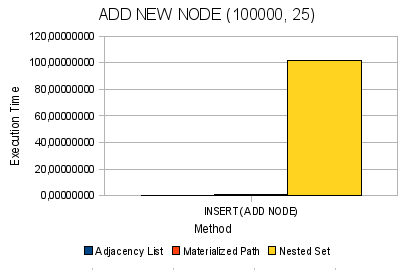
Fig. 6. Adding a new node to the tree
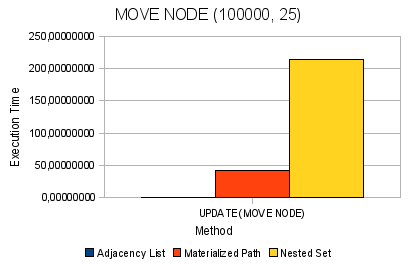
Fig. 7. Moving a node
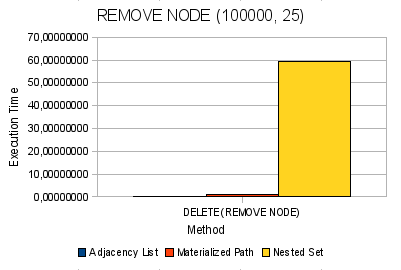
Fig. 8. Removing a node and all its descendants from the tree
Generally, in absolute figures, we can draw the following conclusions:
Adjacency List:
| Knots | ALL | PATH | BRANCH | PARENT | CHILDREN | ADD | MOVE | Remove |
| 100 | 0,00245 | 0,00016 | 0,00416 | 0,00009 | 0,00011 | 0,00059 | 0,00037 | 0,00009 |
| 1000 | 0,00335 | 0,00025 | 0.03579 | 0,00009 | 0,00011 | 0,00387 | 0,00037 | 0,00009 |
| 10,000 | 0,01244 | 0,00058 | 0.38146 | 0,00024 | 0,00036 | 0.03548 | 0,00081 | 0,00011 |
| 100,000 | 0.10798 | 0,00105 | 2,55379 | 0,00155 | 0,00138 | 0.06382 | 0,00119 | 0.13931 |
| 500,000 | 0.62305 | 0,00124 | 43,91373 | 0,00053 | 0,00209 | 0.05232 | 0,00077 | 0,00041 |
Nested Set
| Knots | ALL | PATH | BRANCH | PARENT | CHILDREN | ADD | MOVE | Remove |
| 100 | 0,00020 | 0,00015 | 0,00020 | 0,00017 | 0,00019 | 0,00367 | 0.02285 | 0,00314 |
| 1000 | 0,00129 | 0,00040 | 0,00093 | 0,00017 | 0,00059 | 0.02593 | 0.19237 | 0.02619 |
| 10,000 | 0,01387 | 0,00433 | 0,00825 | 0,01771 | 0,00460 | 0.38235 | 1,37070 | 0.37219 |
| 100,000 | 0.17165 | 0.07634 | 0.14261 | 0.17218 | 0.09953 | 101,749 | 213,461 | 59,1912 |
| 500,000 | 0.83033 | 0.41670 | 0.62517 | 0.42942 | 0.15318 | 1427.96 | 3712.30 | 1627.97 |
Materialized Path
| Knots | ALL | PATH | BRANCH | PARENT | CHILDREN | ADD | MOVE | Remove |
| 100 | 0,00020 | 0,00017 | 0,00020 | 0,00016 | 0,00019 | 0,00076 | 0.02633 | 0,00059 |
| 1000 | 0,00137 | 0,00069 | 0,00107 | 0,00016 | 0,00071 | 0,00136 | 0,22232 | 0,00136 |
| 10,000 | 0.01560 | 0,00608 | 0.01372 | 0,00056 | 0,00737 | 0,00679 | 1,44434 | 0,00801 |
| 100,000 | 0.18680 | 0,10466 | 0.17608 | 0,00064 | 0.18546 | 0.92136 | 41.5875 | 1.06560 |
| 500,000 | 0.99102 | 0.56412 | 0.59418 | 0,00090 | 0.56800 | 2.02149 | 2950.40 | 1.67124 |
Let's think about what they say all these numbers and graphs.
First, all algorithms on small amounts of data (up to 10,000 nodes inclusive) showed quite acceptable performance on all functions.
Secondly, problem operations exist, namely:
Selection of branches entirely in the tree AL. Look, this operation takes up to 2.5 seconds.
I would like to note that we cheated a little in our test. And this is how. In the adjacency list (AL) algorithm, we implemented the path selection method of the multiple JOINs of the table with ourselves. Yes, the result is impressive, especially in comparison with the result of fetching a branch in a recursive way. But you are unlikely to choose such a way of implementing this function for your application. Is that as a temporary optimization. After all, you need to know the maximum level of nesting and not fall under the limitation of the DBMS on the number of JOINs in a single query. We just did a test.
Next, we have problems with node movement operations in NS and MP algorithms ranging from 10,000 nodes in the tree (over 1 second) and then everything gets worse - at 100,000 nodes for MP - this figure is over 40 seconds, for NS - almost 4 minutes. At 500,000 knots, the numbers go beyond all reasonable limits - almost 50 minutes for MP and over 1 hour for NS.
For NS, a similar picture develops in the remaining operations of change. For 10,000 items, the addition takes more than 1.5 minutes, and for 500,000 items, it already takes more than 23 minutes. With removal, the same problem is almost a minute for 100,000 knots and over 27 minutes for 500,000 knots.
MP feels quite confident and on fairly large volumes in the operations of removing and adding nodes. On trees of 100,000 elements, these operations take place within 1 second, which is more than a positive result. And even at 500,000 nodes, these operations occur within a few seconds.
This means that Nested Set should be used with actually static trees, which, if changed, are extremely rare. At the same time, it is worthwhile to think about creating a tool that rebuilds the tree on demand completely, using the AL scheme in the base basis (as our program for generating arbitrary random trees does). This, as evidenced by the facts much faster than the NS routine itself. Or even abandon this algorithm in favor of the Materialized Path.
Conclusion
As we were able to find out, the demand for such algorithms as Nested Set and Materialized Path is due, first of all, to large amounts of data, where they can optimize some search and sample requests that will be critical for the application. Or under high load conditions, where query optimization is also important. In this case, we are talking about the optimization of such operations as finding the path and selecting the entire branch in the Adjacency List tree. In practice, it is also worth talking about optimizing the operations of finding neighbors, choosing the “leaves” of the whole tree or in a branch of a given node, as well as other operations not considered here (which, in fact, are difficult to implement for AL at the level of SQL queries).
Against the background of the results obtained, the Nested Set is qualitatively inferior to the Materialized Path, which feels quite confident in the operations for deletion and addition (and how often do you move nodes in your trees? ...). In addition, I see good prospects for optimizing this algorithm, which we will discuss in the next article.
Good luck in development!
This is a cross-post of the original article from my blog.
Source: https://habr.com/ru/post/47280/
All Articles