Hierarchical Data Structures and Doctrine

Introduction

Storing hierarchical data (or simply trees) in relational structures is quite a non-trivial task and causes some problems when developers encounter a similar task.



First of all, this is due to the fact that relational databases are not adapted for storing hierarchical structures (such as XML files), the structure of relational tables is simple lists. Hierarchical data has a parent-heirs relationship, which is not implemented in a relational structure.

')

However, the task of “storing trees in a database” sooner or later arises before any developer.



Below we consider in detail what approaches exist in organizing the storage of trees in relational databases, and also consider the tools that ORM Doctrine provides for working with such structures.

Adjacent Vertices List (Adjacency List)

Structure description

As a rule, such a data structure involves storing information about the adjacent vertices of our tree. Let's consider the simplest graph with crown vertices (1,2,3):







Fig. 1. A graph with three vertices



As you can see, each element of this graph stores information about the connection with other elements, ie:

  1 - 2.3
 2 - 1.3
 3 - 1.2 

In fact, to build a tree, such a graph is redundant, since for the usual branching structure, we need to keep only the “parent-heir” connection, ie:

  2-1
 3-1 

Then we get a tree with one root element (1) and two branches (2,3):







Fig. 2. Tree graph



In principle, one and the other graphs can, if desired, be displayed in the database using a list of adjacent vertices, but since we are interested in precisely the trees, we’ll dwell on them.



So, in order to store the hierarchical structure in the database using the Adjacency List method, we need to store information on the heir-parent relationship in data tables. Let's look at a real tree example:







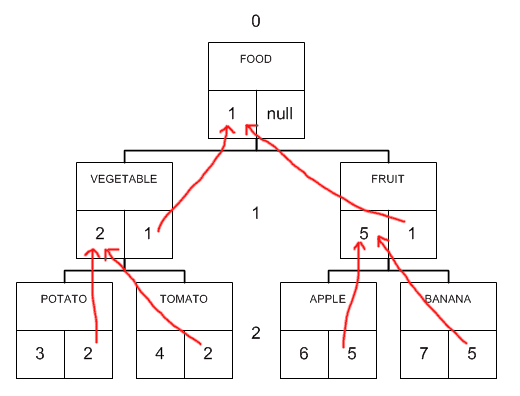
Fig. 3. Tree structure by the method of adjacent vertices



In the figure, squares indicate tree nodes. Each node has a name (upper rectangle inside the square), an identifier (left lower square) and a link to the parent identifier (lower right square). As can be seen from Fig. 3, each heir in such a structure refers to his ancestor. In terms of the database, we can display it as follows in a table:







Fig. 4. Tree data table constructed by the method of the list of adjacent vertices



Or in the form of SQL:

  CREATE TABLE al_tree (
     `id` BIGINT NOT NULL AUTO_INCREMENT PRIMARY KEY,
     `parent_id` BIGINT NULL,
     `name` VARCHAR (50) NOT NULL
 ) TYPE = InnoDB DEFAULT CHARSET = utf8;

 CREATE INDEX fk_tree_tree ON al_tree (parent_id);

 ALTER TABLE al_tree ADD CONSTRAINT fk_tree_tree
     FOREIGN KEY (parent_id) REFERENCES al_tree (id) ON UPDATE CASCADE ON DELETE CASCADE;

 INSERT INTO al_tree VALUES
     (1, NULL, 'FOOD'),
     (2, 1, 'VEGETABLE'),
     (3, 2, 'POTATO'),
     (4, 2, 'TOMATO'),
     (5, 1, 'FRUIT'),
     (6, 5, 'APPLE'),
     (7, 5, 'BANANA'); 

It should be immediately noted that such an algorithm for storing trees has certain advantages and disadvantages. First of all, it is not quite convenient for reading - and this is its main drawback.



Problems with reading from the database are less noticeable if you read the entire tree. This is a fairly simple query:

  SELECT * FROM al_tree ORDER BY id; 

Result:

  + ---- + ----------- + ----------- +
 |  id |  parent_id |  name |
 + ---- + ----------- + ----------- +
 |  1 |  NULL |  FOOD |
 |  2 |  1 |  VEGETABLE |
 |  3 |  2 |  POTATO |
 |  4 |  2 |  TOMATO |
 |  5 |  1 |  FRUIT |
 |  6 |  5 |  APPLE |
 |  7 |  5 |  BANANA |
 + ---- + ----------- + ----------- + 

However, in the future, such a sample implies a rather capacious programmatic post-processing of data. First, you need to recursively rebuild the data, taking into account the connections "ancestor-heir", and only then they can be used to display somewhere.



Another option to read the entire tree:

  SELECT t1.name AS lvl1, t2.name as lvl2, t3.name as lvl3
 FROM al_tree AS t1
 LEFT JOIN al_tree AS t2 ON t2.parent_id = t1.id
 LEFT JOIN al_tree AS t3 ON t3.parent_id = t2.id
 LEFT JOIN al_tree AS t4 ON t4.parent_id = t3.id
 WHERE t1.id = 1; 

The result in this case will be:

  + ------ + ----------- + -------- +
 |  lvl1 |  lvl2 |  lvl3 |
 + ------ + ----------- + -------- +
 |  FOOD |  VEGETABLE |  POTATO |
 |  FOOD |  VEGETABLE |  TOMATO |
 |  FOOD |  FRUIT |  APPLE |
 |  FOOD |  FRUIT |  BANANA |
 + ------ + ----------- + -------- + 

Although the data in this form is already more suitable for output at once, but, as you can see, the main drawback of this approach is that you need to know reliably the number of nesting levels in your hierarchy, besides, the larger the hierarchy, the more JOINs - the lower the performance.



Nevertheless, this method also has significant advantages - it is easy to make changes, change places and delete nodes in a tree.



Conclusion - this algorithm is well applicable if you operate with small tree structures that are often amenable to change.



On the other hand, this algorithm also feels pretty confident with large trees, if you read them in portions of the form “I know a parent - read all the heirs.” A good example of such a case is dynamically loaded trees. In this case, the algorithm is practically optimized for this behavior.



However, it is poorly applicable when you need to read any other pieces of wood, find the paths, the previous and next nodes when going around and read the whole tree branches (to the full depth).

Using a list of contiguous vertices in Doctrine

First I would like to make a few introductory words on the organization of table templates in Doctrine, with the help of which such things are implemented in it. Those who are already familiar with this concept in the doctrine may skip a few paragraphs forward to more interesting things.



So, the entities that we operate in ORM Doctrine are active records ( Active Record ). Those. objects that combine business logic and are able to interact with the database. But the Doctrine developers envisaged extending the functionality of record objects not only by inheritance, but also by applying “patterns of behavior” to these objects. This is implemented by the Doctrine / Template package.



Thus, if there is a need to bring up an active record before any behavior (for example, Versionable - conducts an audit of all changes, I18N - multilingual or NestedSet - a tree-like “nested set”), then this can be done using these templates behavior.



To connect any of the existing templates, it is enough to configure our model properly (via YAML or directly in the code of the base table of the model).



When the time comes, we will show with examples how to do this.



So far, unfortunately, or fortunately, but in the form of a template for tables, the method of the list of adjacent vertices in Doctrine is not implemented. If you wish, you can write the implementation yourself and even offer it to the Doctrine developers, this is up to you.



However, the basic functions that can be implemented within this model can be implemented in Doctrine without using patterns of behavior. Unfortunately, we will not receive functions of work with a tree, but we will be able to solve the main tasks.



To do this, configure our model properly. Using YAML we describe the structure of our table:

  AlTree:
   tableName: al_tree
   columns:
     id:
       type: integer (8)
       primary: true
       autoincrement: true
     name:
       type: string (50)
       notnull: true
     parent_id: integer (8) 

And now the most important thing is to correctly describe the relationships in the table. In the same place with the following line we will write:

  relations:
     Parent:
       class: AlTree
       local: parent_id
       foreign: id
       type: one
     Children:
       class: AlTree
       local: id
       foreign: parent_id
       type: many 

Now we build our model by running the command:

  ./doctrine generate-models-yaml 

Everything. The model is ready. In fact, the same could be done in the already ready BaseAlTree base class:

  <? php
 ...
   public function setUp ()
   {
     $ this-> hasOne ('AlTree as Parent', array ('local' => 'parent_id',
                                             'foreign' => 'id'));

     $ this-> hasMany ('AlTree as Children', array ('local' => 'id',
                                                'foreign' => 'parent_id'));
   }
 ...
 ?> 

Now it's time to enjoy the results of our work. Let's write a simple code that displays a tree constructed with indents on a normal HTML page using recursion.

 <?  / ** * Extract the root of the tree * / $ root = Doctrine :: getTable ('AlTree') -> findByDql ('WHERE parent_id IS NULL') -> getFirst ();  echo '<pre>';  printRTree ($ root);  echo '</ pre>';  / ** * Prints the tree recursively to the screen * * @param AlTree $ node - record object - tree node * @param int $ level - nesting level of the transmitted node * / function printRTree (AlTree $ node, $ level = 0) {/ * * * This line draws our tree * / echo str_repeat ("\ t", $ level).  $ node-> getName ().  "\ n";  / ** * Next we check if there are any heirs, * and if there is, we enter into recursion.  * Pay attention - this is the miracle property of * Children, which we described in the config * of our model!  * / if (($ children = $ node-> Children-> getIterator ()) && $ children-> count ()> 0) {$ level ++;  while (($ child = $ children-> current ())) {/ ** * Entering recursion * / printRTree ($ child, $ level);  $ children-> next ();  }}}?> 

Please note that after we have properly configured the links in our model object, we have the Children and Parent properties available to us. However, any first read access to them generates a query to the database. Therefore, to build large trees in one pass, this approach can be quite expensive.



But at the same time, it is a pleasure to implement a dynamically loadable tree in this way!

Nested Set

Structure description

About this algorithm and its speed, probably, all web developers have heard. Yes, this algorithm is really very good when you need to frequently and a lot refer to the hierarchical data for reading. Consider the essence of this approach.



When building a tree on the basis of nested sets, we will use the principle of traversing this tree from left to right, as shown by the arrows in Fig. 5. To do this, we define for each node of the tree integer keys on the left (lft) and on the right (rgt) (the lower squares inside the node). And distribute integer incremental values ​​to them during the traversal. See what happened.







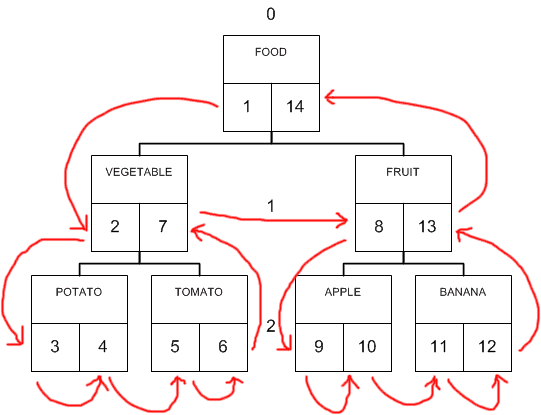
Fig. 5. Nested Set.



The root element received keys 1 and 14, which include the range of numbers of all other keys. VEGETABLE branch received keys 2 and 7, which, in turn, include the entire range of numbers of keys of all its heirs, etc. Here they are - nested sets. It's simple, isn't it?



Let's recreate the same structure in the context of the database table.







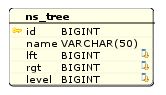
Fig. 6. Table of hierarchical data based on the method of nested sets



Or in the form of SQL:

  CREATE TABLE ns_tree (
     `id` BIGINT NOT NULL AUTO_INCREMENT PRIMARY KEY,
     `name` VARCHAR (50) NOT NULL,
     `lft` BIGINT NOT NULL,
     `rgt` BIGINT NOT NULL,
     `level` BIGINT NOT NULL
 ) TYPE = InnoDB DEFAULT CHARSET = utf8;

 CREATE INDEX nslrl_idx ON ns_tree (lft, rgt, level);

 INSERT INTO ns_tree VALUES
     (1, 'FOOD', 1, 14, 0),
     (2, 'VEGETABLE', 2, 7, 1),
     (3, 'POTATO', 3, 4, 2),
     (4, 'TOMATO', 5, 6, 2),
     (5, 'FRUIT', 8, 13, 1),
     (6, 'APPLE', 9, 10, 2),
     (7, 'BANANA', 11, 12, 2); 

As you can see, we have added one more field to the table - level. It will store information about the nesting level of each branch of the tree. In principle, it is not necessary to do this at all - the nesting level can be quite simply calculated, but since this algorithm is optimized just for reading, why not win in performance by caching the level information? A rhetorical question…



Reading a tree from the database



We read the whole tree:

  SELECT node.id, node.name, node.level
 FROM ns_tree AS node,
 ns_tree AS parent
 WHERE node.lft BETWEEN parent.lft AND parent.rgt
 AND parent.id = 1
 ORDER BY node.lft; 

The result will be:

  + ---- + ----------- + ------- +
 |  id |  name |  level |
 + ---- + ----------- + ------- +
 |  1 |  FOOD |  0 |
 |  2 |  VEGETABLE |  1 |
 |  3 |  POTATO |  2 |
 |  4 |  TOMATO |  2 |
 |  5 |  FRUIT |  1 |
 |  6 |  APPLE |  2 |
 |  7 |  BANANA |  2 |
 + ---- + ----------- + ------- + 

Theoretically, we could get the same result by calculating the nesting level on the fly:

  SELECT node.id, node.name, (COUNT (parent.id) - 1) AS level
 FROM ns_tree AS node,
 ns_tree AS parent
 WHERE node.lft BETWEEN parent.lft AND parent.rgt
 GROUP BY node.name
 ORDER BY node.lft; 

Try to compare the result yourself - it will be identical to the first. Only the request itself is more resource intensive in this case. And since Nested Set is an optimal reading algorithm, a small optimization in the form of caching the nesting level along with the rest of the data is not such a bad strategy.



In the same, rather simple way, we can read whole branches, paths from our tree, bypass its nodes, etc.



For example, if we want to extract all vegetables (VEGETABLE) from our example, it is quite simple to do this:

  SELECT node.id, node.name, node.level
 FROM ns_tree AS node, ns_tree AS parent
 WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.id = 2
 ORDER BY node.lft; 

Moreover, if it is necessary to exclude from the results of the parent itself, you can do several ways:

• adding HAVING level> 1
• adding in the WHERE clause: AND node.id! = 2

or in another way - let it be a creative task for the reader.



Yes, fast and flexible reading, including aggregation with external related data, is a strong point of this algorithm.



However, there is no blessing in disguise, and in this case, significant difficulties begin when we need to make changes to the Nested Set tree or remove any of its branches.



This is due, primarily, to the fact that with changes, we will need to recalculate all the keys of the part of the tree that is located to the right of the node being changed , as well as update the information about nesting levels. And all this is not done in one simple request.



See for yourself.



Adding a new branch



Suppose we want to add a new branch named SEA FOOD to our tree on the same level as VEGETABLES and FRUIT.

  BEGIN;

 SELECT @treeRight: = rgt FROM ns_tree
 WHERE id = 2;  / * to the right of the VEGETABLES branch, which has id = 2 * /

 UPDATE ns_tree SET rgt = rgt + 2 WHERE rgt> @treeRight;
 UPDATE ns_tree SET lft = lft + 2 WHERE lft> @treeRight;

 INSERT INTO ns_tree VALUES (0, 'SEA FOOD', @treeRight + 1, @treeRight + 2, 1);

 COMMIT; 

If you use MYISAM tables in MySQL, or a version that does not support transactions, you can use write locks instead of BEGIN and COMMIT:

  LOCK TABLE ns_tree WRITE;
 ...
 UNLOCK TABLES; 

As you can see, the task of adding a new branch is quite expensive and non-trivial. However, solvable.



Deleting a branch



Let's now try to delete the newly created branch:

  BEGIN;

 SELECT @treeLeft: = lft, @treeRight: = rgt, @treeWidth: = rgt - lft + 1
 FROM ns_tree
 WHERE id = 8;  / * here is the identifier of the new entry named 'SEA FOOD' * /

 DELETE FROM ns_tree WHERE lft BETWEEN @treeLeft AND @treeRight;
 / *
   ATTENTION!
   Please note - we do not delete by id,
   Although in this case it would suit us.
   But in general, we need to remove the entire branch with its contents!
 * /

 UPDATE ns_tree SET rgt = rgt - @treeWidth WHERE rgt> @treeRight;
 UPDATE ns_tree SET lft = lft - @treeWidth WHERE lft> @treeRight;

 COMMIT; 

Conclusion - Nested Set is really good when we need to read the tree structure from the database. At the same time it is equally good for trees of any size.



However, for hierarchical structures that are subject to frequent change, it obviously will not be the optimal choice.

Using Nested Set in Doctrine

But this method is reflected in Doctrine as an implementation of a pattern of behavior that we can attach to our model.



It is quite simple to do this, using the model configuration method via YAML-config or Pramo in the base class code.



YAML:

  NsTree:
   tableName: ns_tree
   actAs: [NestedSet]
   columns:
     id:
       type: integer (8)
       primary: true
       autoincrement: true
     name:
       type: string (50)
       notnull: true
     lft:
       type: integer (8)
       notnull: true
     rgt:
       type: integer (8)
       notnull: true
     level:
       type: integer (8)
       notnull: true 

As you can see, it is enough just to specify actAs: [NestedSet] in the class description.



However, Doctrine provides a more flexible configuration for the NestedSet model. For example, you can store several trees in one table. To do this, you need to enter into the table an additional field in which you will store the root identifier of the tree for each record.



In this case, the configuration should be written as:

  NsTree:
   tableName: ns_tree
   actAs: 
     NestedSet:
       hasManyRoots: true
       rootColumnName: root_id
   columns:
     id:
       type: integer (8)
       primary: true
       autoincrement: true
     root_id:
       type: integer (8)
       notnull: true
     name:
       type: string (50)
       notnull: true
     lft:
       type: integer (8)
       notnull: true
     rgt:
       type: integer (8)
       notnull: true
     level:
       type: integer (8)
       notnull: true 

All the same could be done in the existing base class of the model.



For the first case:

  <? php
 ...
     public function setTableDefinition ()
     {
         ...
         $ this-> actAs ('NestedSet');
        ...
     }
 ...
 ?> 

or:

  <? php
 ...
     public function setTableDefinition ()
     {
         ...
         $ this-> actAs ('Doctrine_Template_NestedSet');
        ...
     }
 ...
 ?> 

For the second case (several trees):

  <? php
 ...
     public function setTableDefinition ()
     {
         ...
         $ options = array ('hasManyRoots' => true,
                          'rootColumnName' => 'root_id');
         $ this-> actAs ('NestedSet', $ options);
        ...
     }
 ...
 ?> 

Note, Doctrine uses 'root_id' as the default field name. Therefore, you do not need to specify this option if it matches the name in your real table. Otherwise you can set it.



Examples of working with Nested Set trees in Doctrine



Extract and print the whole tree on the screen:

  <? php
 $ tree = Doctrine :: getTable ('NsTree') -> getTree () -> fetchTree ();
 echo "<pre>";
 foreach ($ tree as $ node) {
     echo str_repeat ("\ t", $ node ['level']).  $ node ['name'].  "\ n";
 }
 echo "</ pre>";
 ?> 

See how easy it is!



For additional examples and information, you can refer to the official Doctrine documentation, sections 8.2.4 and 8.2.5.

Materialized Path

Structure description

Another rather interesting approach for storing hierarchical structures. The basic idea of ​​the algorithm is to store the full path to the node from the top of the tree. It looks like this:







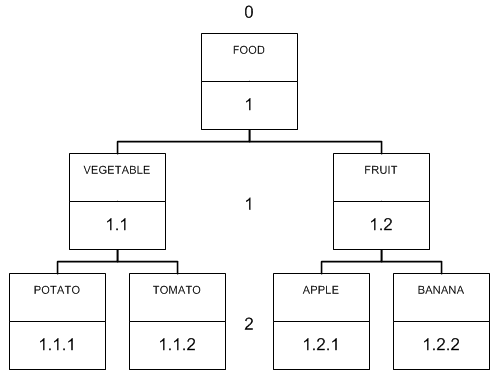
Fig. 7. Tree structure, organized according to the principle “materialized way”



The principle of forming such paths is quite simple. The depth of the path is the level of the tree. Within the branch numbering - incremental. In other words, VEGETABLE is the first child of FOOD, FRUIT is the second child, etc.



It will be easier to look at this in the form of a table:

  + --------------- + ------- +
 |  name |  path |
 + --------------- + ------- +
 |  FOOD |  1 |
 |  VEGETABLE |  1.1 |
 |  POTATO |  1.1.1 |
 |  TOMATO |  1.1.2 |
 |  FRUIT |  1.2 |
 |  APPLE |  1.2.1 |
 |  BANANA |  1.2.2 |
 + --------------- + ------- + 

Perhaps even more clearly.



All this is reflected in the database.







Fig. 8. the structure of the hierarchical data table organized according to the “materialized way” principle



Or in the form of SQL:

  CREATE TABLE mp_tree (
     `id` BIGINT NOT NULL AUTO_INCREMENT PRIMARY KEY,
     `name` VARCHAR (50) NOT NULL,
     `path` VARCHAR (100) NOT NULL
 ) TYPE = InnoDB DEFAULT CHARSET = utf8;

 CREATE INDEX mpp_idx ON mp_tree (`path`);

 INSERT INTO mp_tree VALUES
     (1, 'FOOD', '1'),
     (2, 'VEGETABLE', '1.1'),
     (3, 'POTATO', '1.1.1'),
     (4, 'TOMATO', '1.1.2'),
     (5, 'FRUIT', '1.2'),
     (6, 'APPLE', '1.2.1'),
     (7, 'BANANA', '1.2.2'); 

What is the advantage of this approach?



First, compared to the Nested Set, it is more amenable to change. At the same time, it remains quite convenient for sampling entire trees and their parts. But, and he is not perfect. Especially in the search for the ancestors of the branch.



Search for a node path:

  SELECT t1.name from mp_tree t1, mp_tree t2
 WHERE t2.path like CONCAT (t1.path, '.%')
 AND t2.id = 3;  / * Search for the path to the node named 'POTATO' * / 

Result:

  + ----------- +
 |  name |
 + ----------- +
 |  FOOD |
 |  VEGETABLE |
 + ----------- + 

Calculate nesting level.



To solve this problem, we basically need to count the number of points (or other separators, if you use a non-point) in the paths. Unfortunately, MySQL does not have a suitable function, but we can implement it quite simply on our own:

  CREATE FUNCTION STRFIND (str VARCHAR (255), delimtr CHAR (1)) RETURNS INT
 BEGIN
 DECLARE _cnt INT;
 DECLARE _start INT;
 SET _cnt = -1;
 SET _start = 1;
 WHILE _start> 0 DO
   SET _start = LOCATE (delimtr, str);
   SET str = SUBSTRING (str, _start + 1);
   SET _cnt = _cnt + 1;
 END WHILE;
 RETURN _cnt;
 END 

Branch selection:

  SELECT name, strfind (path, '.') AS level 
 FROM mp_tree 
 WHERE path LIKE '1.1%';  / * Select the entire 'VEGETABLES' branch * /; 

Result:

  + ----------- + ------- +
 |  name |  level |
 + ----------- + ------- +
 |  VEGETABLE |  1 |
 |  POTATO |  2 |
 |  TOMATO |  2 |
 + ----------- + ------- + 

Please note that in this example we used our samopisnaya function and it was quite convenient.



Parent Search:

  SELECT t2. * 
 FROM mp_tree t1, mp_tree t2 
 WHERE t1.id = 3 AND t2.path = SUBSTRING (t1.path, 1, (LENGTH (t1.path) - LOCATE ('.', REVERSE (t1.path))))); 

As you can see, all these requests do not make maximum performance (compared to the previous method), but, nevertheless, the use of this particular algorithm can be much more convenient for trees, on which both read operations and changes are often performed.



As far as the author knows, the algorithm feels pretty confident on fairly large amounts of data.



It should be noted that the most unpleasant in this algorithm will be the operation of inserting a node into the middle of an already existing structure (between other nodes), since this will change all the paths in the underlying nodes. Although, in fairness, it should be said that such an operation will be non-trivial for any data storage model. Another major operation is transferring one branch to another.



But deleting, adding to the end or changing the node - these operations are quite simple, and, as a rule, do not cause difficulties in this model.



As can be seen from the examples, this algorithm can also be somewhat optimized for reading by introducing another level field, as was done for the lists of adjacent vertices (Nested Set). However, it will somewhat complicate the operations of adding, changing and deleting tree nodes, since levels will have to be recalculated for the whole or part of the tree with each change. Ultimately, it is the developer who decides which way to skew the performance.

Use in Doctrine

Unfortunately, at the moment, this method of storing trees has not yet found its implementation in ORM Doctrine (the current version at the time of writing this material is 1.0.4, 1.1.0 — it also has no implementation in the alpha version).



Nevertheless, there are all prerequisites for believing that its implementation will appear in the future, since the source code of the library contains in the Doctrine / Tree package an abstract empty class called MaterializedPath.



The author will follow the events and update this article as soon as the implementation is reflected, so you can return here later.

Combined approach

In fact, it should be noted that the above methods can be combined only in two directions:

• Adjacency List + Materialized Path
• Adjacency Lists + Nested Sets (Adjacency List + Nested Set)

Combining the same Nested Set and Materialized Path does not make much sense, because There is no significant gain in reading or writing.



In fact, combining approaches at the database level is limited to entering a field that stores a link to the parent entry in the adjacency list tables and materialized paths:







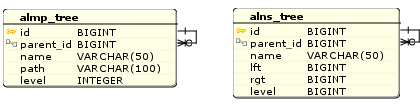
Fig. 9. Tables of models of hierarchical data structures AL + MP and AL + NS



The implications of this approach are obvious.



AL + MP



For AL when used with MP:

• Entire branch and subtree sampling operations are improved.
• Worsening branch transfer operations

For MP when used with AL:

• Improved parent sampling operations for a given node
• Improved selection of the heirs of a given node

AL + NS



For the AL + NS bundle, reciprocity is not so obvious. This is primarily due to the fact that the disadvantages of the problems of changing tree nodes in the NS model completely kill all the advantages of AL in this area. This means that such a bundle should be considered only as a qualitative improvement in the search for parents and heirs of a given node in the NS algorithm, and also as an increase in the reliability of the algorithm itself (the keys can always be rebuilt in the event of damage - the information about the links is stored in AL). The statement about the increase in reliability is true for the previous combination of methods. But this is also a qualitative improvement, although not so obvious, is it?

Conclusion

In this article, we looked at several basic methods for storing hierarchical data in relational databases and outlined all their advantages and disadvantages. We also showed in practice which of them are available for use in the implementation of the Doctrine ORM, and how to use them.



Obviously, even choosing one method or another in each specific case is not a simple task, but the author hopes that this material will facilitate the adoption of a conscious and correct decision, and will also contribute to the creative process of finding new and more optimal solutions.



Good luck in development!

_{PS This is a cross-post of the original article from my blog.}